使用 cubic-bezier() 的高级 CSS 动画

在处理复杂的 CSS 动画时，人们往往会@keyframes使用大量的声明来创建扩展动画。不过，我想分享一些技巧，它们或许能让事情变得更简单，同时又不失原始的 CSS 风格：

多个动画
计时功能

第一个方法使用更广泛，也更为人熟知，而第二个方法则不太常见。这其中可能有充分的理由——用逗号串联动画比理解各种可用的计时函数及其功能相对容易。有一个特别简洁的计时函数，它让我们可以完全控制创建自定义计时函数。cubic-bezier()在这篇文章中，我将向你展示它的强大功能，以及如何使用它来创建精美的动画，而无需过多的复杂性。

让我们从一个简单的例子开始，展示如何将球移动到有趣的方向，比如无穷大（∞）形状：

如你所见，代码并不复杂——只有两个关键帧和一个“奇怪”的cubic-bezier()函数。然而，我们最终得到的是一个看起来相当复杂的无限形状动画。

很酷吧？让我们深入研究一下！

cubic-bezier() 函数

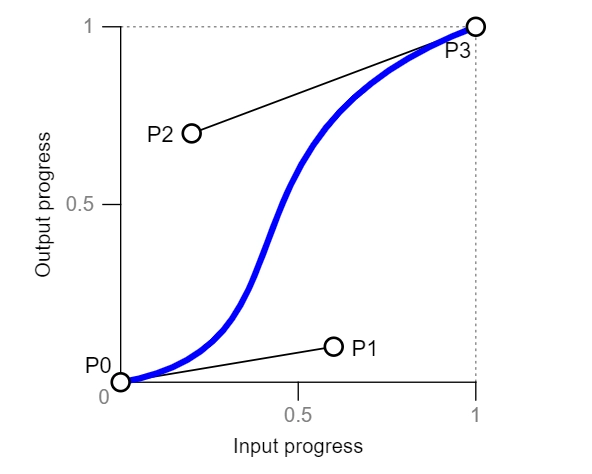
让我们从官方定义开始：

三次贝塞尔缓动函数是一种由四个实数定义的缓动函数，这四个实数指定三次贝塞尔曲线的两个控制点 P1 和 P2，该曲线的端点 P0 和 P3 分别固定在 (0, 0) 和 (1, 1)。P1 和 P2 的 x 坐标限制在 [0, 1] 范围内。

上面的曲线定义了输出（y轴）如何基于时间（x轴）变化。每个轴的范围为 $[0, 1]$ （或 $[0\%, 100\%]$ ）。如果我们有一个持续两秒的动画（ $2秒$ ），则：

0 (0\%) = 0s \newline 1 (100\%) = 2s

如果我们想要动画从5px到20px，那么：

0 (0\%) = 5px \newline 1 (100\%) = 20px

X，时间，总是被限制在 $[0, 1]$ ；然而，输出 Y 可以超越 $[0, 1]$ 。

我的目标是调整 P1 和 P2 以创建以下曲线：

你可能认为这是不可能实现的，因为正如定义中所述， $P_0$ 和 $P_3$ 固定在 $(0,0)$ 和 $(1,1)$ 意味着它们不能位于同一轴上。确实如此，我们会使用一些数学技巧来“近似”它们。

抛物线

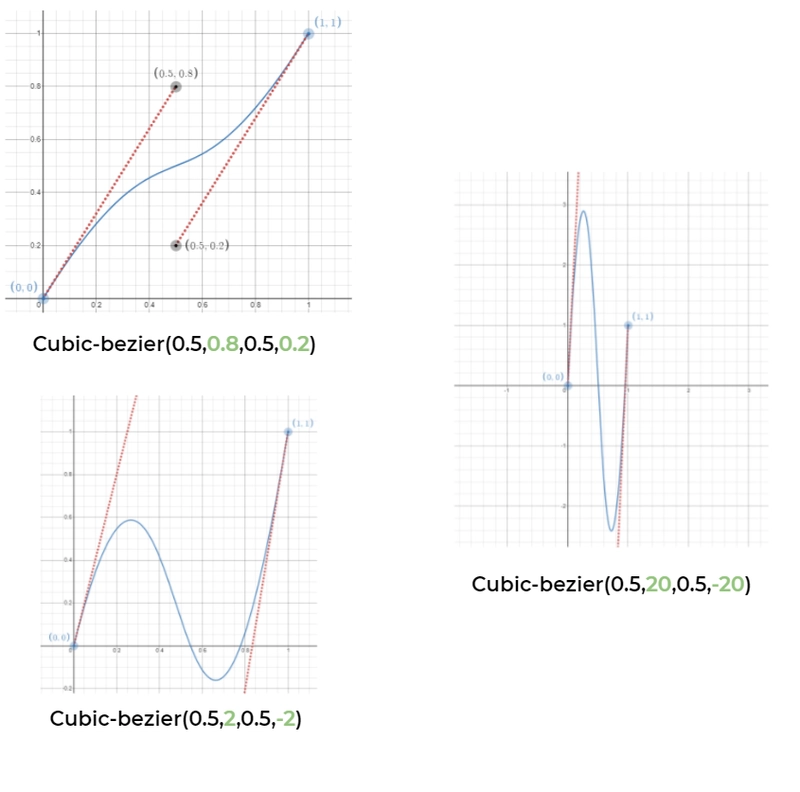
让我们从以下定义开始：cubic-bezier(0,1.5,1,1.5)。这给了我们以下曲线：

我们的目标是 $(1,1)$ 并使其 $(0,1)$ 这在技术上是不可能的。所以我们会尝试伪造它。

我们之前说过我们的范围是 $[0, 1]$ （或 $[0\%, 100\%]$ ) 让我们想象一下 $0\%$ 非常接近 $100\%$ 。例如，如果我们想要动画顶部从 $20px$ ( $0\%$ ）至 $20.1px$ ( $100\%$ ），那么我们可以说初始状态和最终状态是相等的。

嗯，但是我们的元素根本不会移动，对吗？

嗯，它会移动一点，因为 Y 值超过 $20.1px$ ( $100\%$ ）。但这还不足以让我们感受到可察觉的运动：

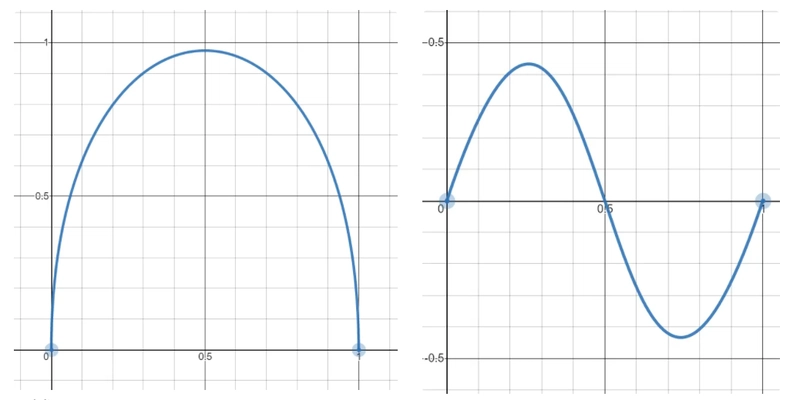
让我们更新曲线并使用cubic-bezier(0,4,1,4)。注意我们的曲线比以前高得多：

曲线	输出

但仍然没有动静——即使最高值已经超过 $3$ （或 $300\%$ ）。让我们尝试一下cubic-bezier(0,20,1,20)：

曲线	输出

是的！它开始移动了一点。你注意到每次增加值时曲线的变化了吗？这说明了我们的观点 $(1,1)$ “视觉上”更接近 $(0,1)$ 当我们缩小时可以看到完整的曲线，这就是诀窍。

通过使用cubic-bezier(0,V,1,V)where $V$ 是一个非常大的值，并且初始状态和最终状态都非常接近（或几乎相等），我们可以模拟抛物线曲线。

一个例子胜过千言万语：

我把“神奇”的三次贝塞尔函数应用到了顶部动画上，并在左侧动画上应用了一个线性函数。这样就得到了我们想要的曲线。

深入数学

对于那些数学爱好者，我们可以进一步分解这个解释。三次贝塞尔曲线可以用以下公式定义：

P = (1−t)^3P_0 + 3(1−t)^2tP_1 + 3(1−t)t^2P_2 + t^3P_3

每个点的定义如下：

P_0 = (0,0), P_1 = (0,V) \newline P_2 = (1,V), P_3 = (1,1)

这给了我们 x 和 y 坐标的两个函数：

X(t) = 3(1−t)t^2 + t^3 = 3t^2 - 2t^3

Y(t) = 3(1−t)^2tV +3(1−t)t^2V + t^3 = t^3 - 3Vt^2 + 3Vt

$V$ 是我们最大的价值， $t$ 在范围内 $[0, 1]$ 。如果我们考虑前面的例子， $Y(t)$ top将给出 $X(t)$ 是时间进度。点 $(X(t),Y(t))$ 将定义我们的曲线。

让我们找到 $Y(t)$ 。为此，我们需要找到 $t$ 将给我们 $Y'(t) = 0$ （当导数等于 $0$ ):

Y'(t) = 3t^2 - 6Vt + 3V

$Y'(t) = 0$ 是二次方程。我就不说无聊的部分了，直接给出结果，就是

t = V - \sqrt{V^2 - V}

什么时候 $V$ 是一个较大的值， $t$ 将等于 $0.5$ 。所以， $Y(0.5) = Max$ 和 $$ $$ $X(0.5)$ 等于 $0.5$ 。这意味着我们在动画的中间点达到最大值，这符合我们想要的抛物线曲线。

还， $Y(0.5)$ 将给出 $\frac{1 + 6V}{8}$ 这将使我们能够根据以下条件找到最大值 $V$ 。由于我们总是使用较大的值 $V$ ，我们可以简化为 $\frac{6V}{8} = 0.75V$ 。

我们使用了 $V = 500$ ，所以最大值是 $375$ （或 $37500\%$ ），我们得到以下结果：

初始状态（ $0$ ):top: 200px
最终状态（ $1$ )：top: 199.5px

有区别 $-0.5px$ 之间 $0$ 和 $1$ 我们称之为增量。对于 $375$ （或 $37500%$ ）我们有一个方程 $375*-0.5px = -187.5px$ 。我们的动画元素正在到达top: 12.5px（ $200px - 187.5px$ ），并给出以下动画：

top: 200px (at 0% of the time ) → top: 12.5px (at 50% of the time) → top: 199.5px (at 100% of the time)

或者，换一种说法：

top: 200px (at 0%) → top: 12.5px (at 50%) → top: 200px (at 100%)

让我们反过来想一下。 $V$ 来让元素到达目标top: 0px？动画将会执行200px → 0px → 199.5px，所以我们需要 $-200px$ 到达 $0px$ 。我们的增量始终等于 $-0.5px$ 。最大值等于 $\frac{200}{0.5} = 400$ ，所以 $0.75V = 400$ 这意味着 $V = 533.33$ 。

我们的元素正在触及顶峰！

下图总结了我们刚才所做的计算：

正弦曲线

我们将使用几乎完全相同的技巧来创建正弦曲线，但公式不同。这次我们将使用cubic-bezier(0.5,V,0.5,-V)

像我们之前所做的那样，让我们看看当我们增加值时曲线将如何演变：

我想你现在可能明白了。使用大值 $V$ 使我们接近正弦曲线。

这是另一个具有连续动画的动画——真正的正弦动画！

数学

让我们开始计算吧！按照与之前相同的公式，我们将得到以下函数：

X(t) = \frac{3}{2}(1−t)^2t + \frac{3}{2}(1−t)t^2 + t^3 = \frac{3}{2}t - \frac{3}{2}t^3 + t^3

Y(t) = 3(1−t)^2tV - 3(1−t)t^2V + t^3 = (6V + 1)t^3 - 9Vt^2 + 3Vt

这次我们需要找到 $Y(t)$ 。 $Y'(t) = 0$ 将给出两个解。解完后：

Y'(t) = 3(6V + 1)t^2 - 18Vt + 3V = 0

…我们得到：

t' = \frac{3V + \sqrt{3V² - V}}{6V + 1}, t'' = \frac{3V - \sqrt{3V² - V}}{6V + 1}

对于较大的值 $V$ ，我们有 $t'=0.211$ 和 $t''=0.789$ 。这意味着 $Y(0.211) = Max$ 和 $$ $$ $Y(0.789) = Min$ 。这也意味着 $X(0.211)= 0.26$ 和 $X(0.789) = 0.74$ 。换句话说，我们达到最大值 $26\%$ 的时间，最低 $74\%$ 的时间。

$Y(0.211)$ 等于 $0.289V$ 和 $Y(0.789)$ 至 $-0.289V$ 。我们根据以下情况进行了一些四舍五入，得出了这些值： $V$ 很大。

我们的正弦曲线也应该与 x 轴相交（或 $Y(t) = 0$ ）一半的时间（或 $X(t) = 0.5$ ）。为了证明这一点，我们使用 $Y(t)$ ——应该等于 $0$ — 所以 $Y''(t) = 0$ 。

Y''(t) = 6(6V + 1)t - 18V = 0

解决方案是 $\frac{3V}{6V + 1}$ ，并且对于一个大 $V$ 值，解决方案是 $0.5$ 。这给了我们 $Y(0.5) = 0$ 和 $X(0.5) = 0.5$ 证实了我们的曲线与 $(0.5,0)$ 点。

现在让我们考虑前面的例子，并尝试找到 $V$ 让我们回到top: 0%。我们有：

初始状态（ $0$ ):top: 50%
最终状态（ $1$ )：top: 49.9%
增量： $-0.1\%$

我们需要 $-50\%$ 达到top: 0%，所以 $0.289V*-0.1\% = -50\%$ 这使得我们 $V = 1730.10$ 。

正如您所见，我们的元素触及顶部并消失在底部，因为我们有以下动画：

top: 50% → top: 0% → top: 50% → top: 100% → top: 50% → and so on ...

用一个数字来总结一下计算：

举个例子来说明所有的曲线：

是的，你看到了四条曲线！如果你仔细看，你会发现我用了两种不同的动画，一种是 $49.9\%$ （增量为 $-0.01\%$ )，另一个则 $50.1\%$ （增量为 $+0.01\%$ ）。通过改变增量的符号，我们可以控制曲线的方向。我们还可以控制三次贝塞尔曲线的其他参数（不包括 $V$ 应该保持较大的值）以从相同的曲线创建更多变化。

下面是一个交互式演示：

回到我们的例子

让我们回到最初的例子，一个球以无穷大符号的形状移动。我只是简单地组合了两个正弦动画来实现它。

如果我们将之前的方法与多重动画的概念结合起来，就能得到令人惊叹的效果。这里再次展示最初的例子，这次是一个交互式演示。更改一下这些值，看看效果如何：

让我们更进一步，添加一点 CSS Houdini。借助它，我们可以为复杂的变换声明制作动画@property（但 CSS Houdini 目前仅限于 Chrome 和 Edge 支持）。

你能用它画出什么样的画？以下是我画的一些：

这是一个螺旋图动画：

还有一个没有 CSS Houdini 的版本：

从这些例子中我们可以得出以下几点结论：

每个关键帧仅使用一个包含增量的声明来定义。
元素的位置和动画是独立的。我们可以轻松地将元素放置在任何位置，而无需调整动画。
我们没有进行任何计算。没有大量的角度或像素值。我们只需要关键帧中的一个小值和cubic-bezier()函数中的一个大值。
只需调整持续时间值即可控制整个动画。

那么过渡呢？

相同的技术也可以用于 CSS 的 transition 属性，因为它在时间函数方面遵循相同的逻辑。这很棒，因为我们可以在创建一些复杂的悬停效果时避免使用关键帧。

以下是我没有使用关键帧制作的动画。如果你关注我的话，你会记得它们属于我的下划线/叠加动画合集😉

马里奥跳跃的动画得益于抛物线曲线。我们完全不需要关键帧来创建悬停时的抖动动画。正弦曲线完全可以胜任所有工作。

这是另一个版本的马里奥，这次使用了 CSS Houdini。没错，由于抛物线的缘故，他仍然在跳跃：

为了更进一步，这里还有更多无需关键帧的精美悬停效果（同样，仅限 Chrome 和 Edge）。剧透一下我的下一个系列😜

就是这样！

现在你已经掌握了一些神奇的cubic-bezier()曲线以及它们背后的数学原理。当然，好处在于，像这样的自定义时间函数让我们能够制作精美的动画，而无需像往常一样使用复杂的关键帧。

我明白并非每个人都擅长数学，这没关系。有一些工具可以提供帮助，比如 Matthew Lein 的Ceaser，它允许你拖动曲线点来获得所需的效果。另外，如果你还没有收藏cubic-bezier.com ，也可以访问它。如果你想在 CSS 之外尝试 cubic-bezier，我推荐desmos，在那里你可以查看一些数学公式。

无论您如何获得您的cubic-bezier()价值观，希望现在您已经了解它们的力量以及它们如何在过程中帮助编写更好的代码。

文章来源：https://dev.to/this-is-learning/advanced-css-animation-using-cubic-bezier-nho