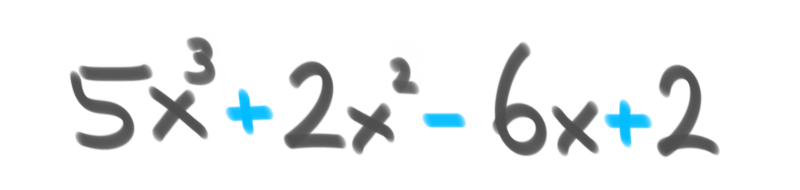咖啡休息时间介绍算法的时间复杂度

那么“时间复杂度”到底是什么呢？

确定时间复杂度

P 与 NP、NP 完全问题和 NP 难问题

在编写代码之前估算算法的效率

提高现有代码的时间复杂度

来源

就像编写第一个for循环一样，理解时间复杂度是学习如何编写高效复杂程序的重要里程碑。你可以把它想象成一种超能力，让你在运行任何一行代码之前就能准确地知道在特定情况下哪种类型的程序可能是最高效的。

复杂性分析的基本概念非常值得学习。你将能够更好地理解你正在编写的代码如何与程序的输入交互，从而减少编写缓慢且问题重重的代码所浪费的时间。你很快就能了解所有需要了解的知识，从而开始编写更高效的程序——事实上，我们大约十五分钟就能搞定。你现在就可以去喝杯咖啡（或者茶，如果你喜欢的话），我会在你的咖啡时间结束前带你了解一下。去吧，我等着。

都准备好了吗？开始吧！

那么“时间复杂度”到底是什么呢？

算法的时间复杂度是该算法处理某个输入所需时间的近似值。它通过操作的数量来描述算法的效率。这与操作重复的次数不同；我稍后会对此进行详细说明。通常，算法的操作越少，速度就越快。

我们用大 O 符号来表示时间复杂度，类似于O ( n )。它的正式定义涉及相当多的数学知识，但通俗地说，大 O 符号给出了算法在最坏情况下的近似运行时间，或者换句话说，它的上限。^[2]它本质上是相对的和比较的。^{[3]我们描述的是算法相对于其输入数据}n的增加的效率。如果输入是一个字符串，那么n就是字符串的长度。如果它是一个整数列表，那么n就是列表的长度。

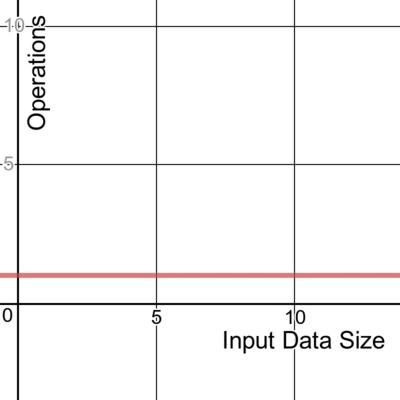
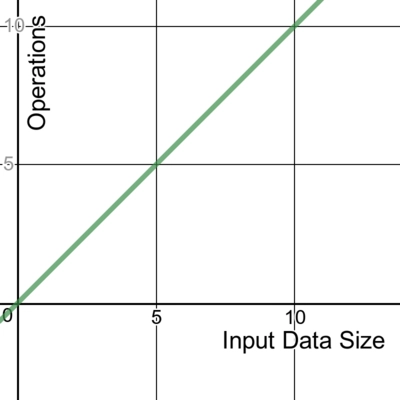
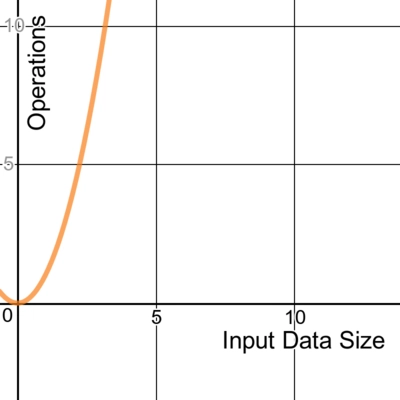
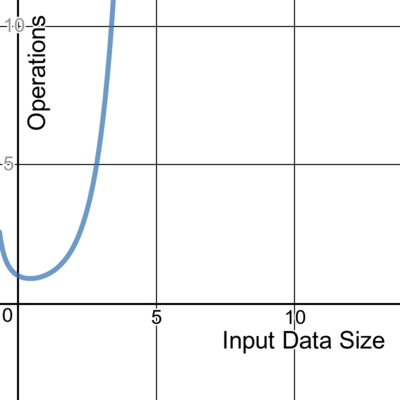
用图表来描绘大 O 符号所代表的含义是最容易的：

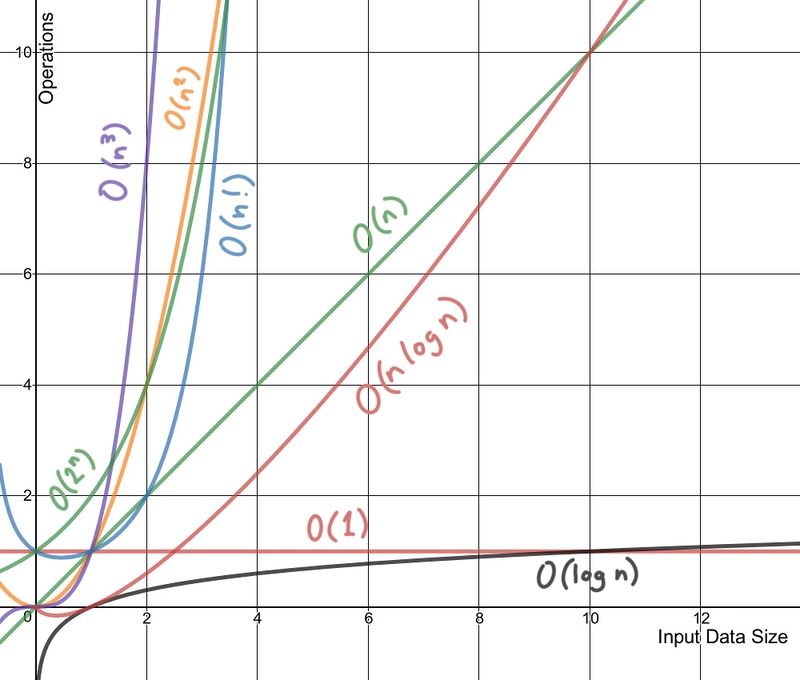
使用非常优秀的 Desmos 图形计算器绘制的线条。您可以点击此处试用此图表。

阅读本文其余部分时，请记住以下要点：

时间复杂度是一个近似值
算法的时间复杂度接近其最坏情况的运行时间

确定时间复杂度

我们可以利用不同类别的复杂度来快速理解算法。我将使用嵌套循环和其他示例来说明其中一些类别。

多项式时间复杂度

多项式（polynomial）源于希腊语poly ，意为“许多”，拉丁语nomen，意为“名称”。它描述的是一个由常数变量以及加法、乘法和非负整数幂的幂运算组成的表达式。^[4]这是一种非常数学化的说法，它包含通常用字母和符号表示的变量，如下所示：

以下课程描述多项式算法。其中一些课程包含食品示例。

持续的

恒定时间算法不会根据输入数据改变其运行时间。无论接收的数据大小如何，算法的运行时间都相同。我们将其时间复杂度表示为O (1)。

下面是一个常量算法的示例，它获取切片中的第一个项。

func takeCupcake(cupcakes []int) int {
    return cupcakes[0]
}

可选口味有：香草纸杯蛋糕、草莓纸杯蛋糕、薄荷巧克力纸杯蛋糕、柠檬纸杯蛋糕和“wibbly wobbly, timey wimey”纸杯蛋糕。

有了这种恒定时间算法，无论有多少个纸杯蛋糕，你都只能买第一个。算了，反正口味也太重要了。

线性

线性算法的运行时间是恒定的。它将通过n次运算来处理输入。这通常是时间复杂度最佳（最高效）的情况，因为必须检查所有数据。

下面是时间复杂度为O ( n )的代码示例：

func eatChips(bowlOfChips int) {
    for chip := 0; chip <= bowlOfChips; chip++ {
        // dip chip
    }
}

下面是另一个时间复杂度为O ( n )的代码示例：

func eatChips(bowlOfChips int) {
    for chip := 0; chip <= bowlOfChips; chip++ {
        // double dip chip
    }
}

循环内的代码执行一次、两次还是任意次数都没有关系。这两个循环都以常数因子n来处理输入，因此可以描述为线性的。

不要在共用的碗中蘸两次。

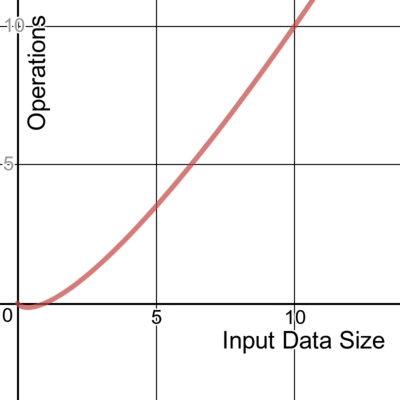
二次函数

下面是一个时间复杂度为O ( n2 )^的代码示例：

func pizzaDelivery(pizzas int) {
    for pizza := 0; pizza <= pizzas; pizza++ {
        // slice pizza
        for slice := 0; slice <= pizza; slice++ {
            // eat slice of pizza
        }
    }
}

由于有两个嵌套循环，或者说嵌套线性运算，该算法对输入n进行²次处理。

立方体

扩展前面的例子，这个具有三个嵌套循环的代码的时间复杂度为^O( n3 )：

func pizzaDelivery(boxesDelivered int) {
    for pizzaBox := 0; pizzaBox <= boxesDelivered; pizzaBox++ {
        // open box
        for pizza := 0; pizza <= pizzaBox; pizza++ {
            // slice pizza
            for slice := 0; slice <= pizza; slice++ {
                // eat slice of pizza
            }
        }
    }
}

不过说真的，谁会送没切片的披萨呢？

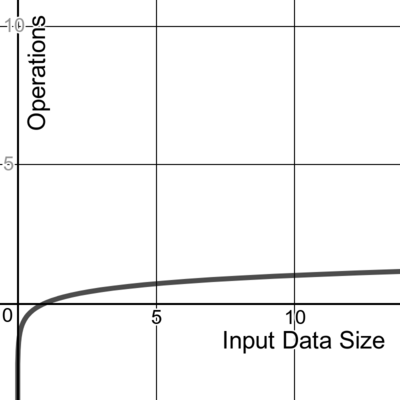
对数

对数算法是指在每一步都减少输入大小的算法。
我们将其时间复杂度表示为O (log n )，其中对数函数log 的形状如下：

一个例子是二分查找算法，它用于查找已排序数组中元素的位置。假设我们要查找元素x ，它的工作原理如下：

如果x与数组中间元素m匹配，则返回m的位置
如果x与m不匹配，则查看m是否大于或小于x
- 如果大于 m，则丢弃所有大于m 的数组项
- 如果较小，则丢弃所有小于m 的数组项
继续对剩余数组重复步骤 1 和 2，直到找到x

我发现理解二分查找最清晰的类比是想象在书店货架上查找书籍的过程。如果书籍按作者姓氏排列，而你想找到“Terry Pratchett”，那么你就知道需要查找“P”部分。

你可以走到过道任意一处书架，看看作者的姓氏。如果你正在看尼尔·盖曼的书，你知道你可以忽略左边的其他书，因为字母表中“G”之前的字母都不是“P”。然后，你可以沿着过道向右移动，重复这个过程，直到找到特里·普拉切特的书区。如果你在任何一家正规书店，这个书区应该相当大，因为他写了好多书。

准线性

在排序算法中，时间复杂度O ( n log n ) 常常用于描述一种数据结构，其中每个操作需要O ( log n ) 的时间。快速排序就是一个例子，它是一种分而治之的算法。

快速排序的原理是将未排序的数组分割成更易于处理的小块。它会先对子数组进行排序，从而对整个数组进行排序。想象一下，这就像尝试将一副牌按顺序排列。如果你把牌分开，然后找五个朋友帮忙，速度会更快。

非多项式时间复杂度

以下类别的算法是非多项式的。

阶乘

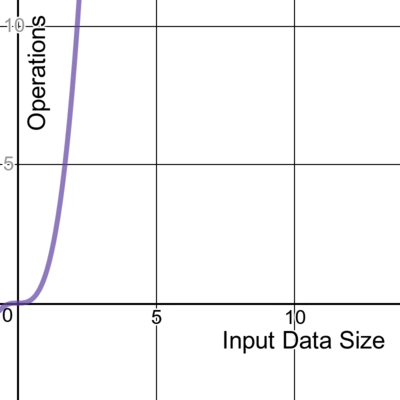
时间复杂度为O ( n !)的算法通常会遍历输入元素的所有排列。一个常见的例子是旅行商问题中的暴力搜索。它试图通过列举所有可能的排列并找出成本最低的排列，找到多个点之间成本最低的路径。

指数

指数算法通常也会迭代输入元素的所有子集。它表示为O (2n ⁾，常见于暴力算法中。它与阶乘时间类似，只是增长率呈指数级增长，这一点您可能并不感到惊讶。数据集越大，曲线越陡峭。

在密码学中，暴力破解可以通过迭代子集来系统地检查密码的所有可能元素。使用指数算法进行此操作，暴力破解长密码比破解短密码耗费的资源极其巨大。这也是为什么长密码被认为比短密码更安全的原因之一。

还有一些不太常见的时间复杂度类别，我不会在这里介绍，但您可以阅读这些类别并在此便捷的表格中找到示例。

递归时间复杂度

正如我在用苹果派解释递归的文章中所描述的，递归函数在特定条件下调用自身。它的时间复杂度取决于函数被调用的次数以及单次函数调用的时间复杂度。换句话说，它是函数运行次数与单次执行时间复杂度的乘积。

这是一个递归函数，它会不断吃馅饼，直到没有馅饼剩下为止：

func eatPies(pies int) int {
    if pies == 0 {
        return pies
    }
    return eatPies(pies - 1)
}

单次执行的时间复杂度是常数。无论输入多少个饼，程序都会做同样的事情：检查输入是否为 0。如果是，则返回；如果不是，则调用自身，并传入少一个饼。

初始馅饼的数量可以是任意数量，并且我们需要处理所有馅饼，因此可以将输入描述为n。因此，该递归函数的时间复杂度为O ( n )。

该函数的返回值为零，加上一些消化不良。

最坏情况时间复杂度

到目前为止，我们已经讨论了一些嵌套循环的时间复杂度，并给出了一些代码示例。然而，大多数算法都是由这些元素的多种组合构成的。我们如何确定一个包含许多此类元素的算法的时间复杂度呢？

很简单。我们可以通过找出算法所有部分中最大的复杂度来描述算法的总时间复杂度。这是因为代码中最慢的部分是瓶颈，而时间复杂度关注的是描述算法运行时间的最坏情况。

假设我们有一个用于办公室聚会的程序。如果我们的程序如下所示：

package main

import "fmt"

func takeCupcake(cupcakes []int) int {
    fmt.Println("Have cupcake number",cupcakes[0])
    return cupcakes[0]
}

func eatChips(bowlOfChips int) {
    fmt.Println("Have some chips!")
    for chip := 0; chip <= bowlOfChips; chip++ {
        // dip chip
    }
    fmt.Println("No more chips.")
}

func pizzaDelivery(boxesDelivered int) {
    fmt.Println("Pizza is here!")
    for pizzaBox := 0; pizzaBox <= boxesDelivered; pizzaBox++ {
        // open box
        for pizza := 0; pizza <= pizzaBox; pizza++ {
            // slice pizza
            for slice := 0; slice <= pizza; slice++ {
                // eat slice of pizza
            }
        }
    }
    fmt.Println("Pizza is gone.")
}

func eatPies(pies int) int {
    if pies == 0 {
        fmt.Println("Someone ate all the pies!")
        return pies
    }
    fmt.Println("Eating pie...")
    return eatPies(pies - 1)
}

func main() {
    takeCupcake([]int{1, 2, 3})
    eatChips(23)
    pizzaDelivery(3)
    eatPies(3)
    fmt.Println("Food gone. Back to work!")
}

我们可以用代码最复杂部分的复杂度来描述整个代码的时间复杂度。该程序由我们已经见过的函数组成，其时间复杂度等级如下：

功能	班级	大O
`takeCupcake`	持续的	零（1）
`eatChips`	线性	在）
`pizzaDelivery`	立方体	O（n3）
`eatPies`	线性（递归）	在）

为了描述整个办公室聚会程序的时间复杂度，我们选择最坏的情况。该程序的时间复杂度为^O( n³ )。

这是办公室聚会的配乐，只是为了好玩。

Have cupcake number 1
Have some chips!
No more chips.
Pizza is here!
Pizza is gone.
Eating pie...
Eating pie...
Eating pie...
Someone ate all the pies!
Food gone. Back to work!

P 与 NP、NP 完全问题和 NP 难问题

你可能会在探索时间复杂度时遇到这些术语。通俗地说，P（多项式时间）是指一类可以快速解决的问题。NP （非确定性多项式时间）是指一类可以在多项式时间内快速验证答案的问题。NP 不仅包含 P，还包含另一类称为NP 完全的问题，这类问题目前尚无快速解决方案。^[5]除了 NP 完全问题之外，还有另一类称为NP 难的问题，这类问题尚未找到可验证的多项式算法解决方案。^[6]

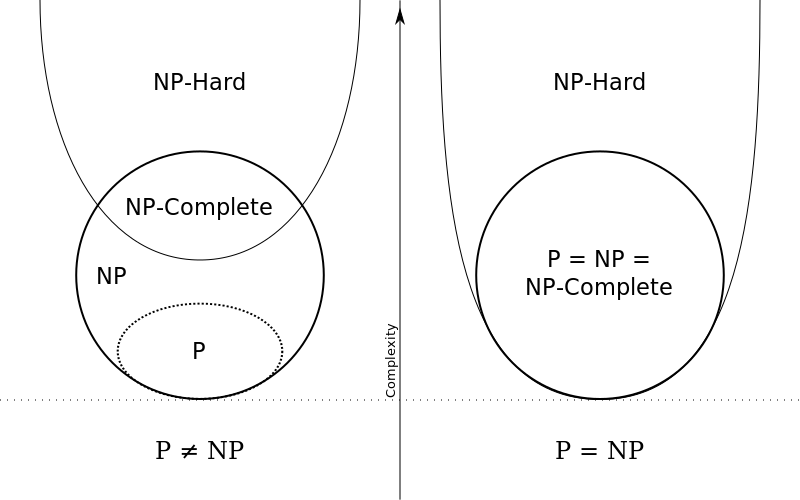
P 与 NP 欧拉图，作者：Behnam Esfahbod，CC BY-SA 3.0

P 与 NP是计算机科学中一个尚未解决的开放性问题。

无论如何，你通常不需要了解NP和NP难问题就能开始利用时间复杂度的优势。它们是另一个潘多拉魔盒。

在编写代码之前估算算法的效率

到目前为止，我们已经确定了一些不同的时间复杂度类别，以及如何确定算法属于哪一类。那么，在编写任何需要评估的代码之前，这些知识对我们有什么帮助呢？

结合一些时间复杂度的知识以及对输入数据大小的了解，我们可以猜测在给定时间限制内处理数据的有效算法。我们的估算可以基于现代计算机每秒可以执行数亿次运算的事实。^[1]下表摘自《竞技程序员手册》，提供了在一秒时间内处理相应大小输入所需的时间复杂度估算。

输入尺寸	1s 处理时间所需的时间复杂度
n≤10	在！）
n≤20	O（²ⁿ）
n≤500	O（n3）
n≤5000	O（n²）
n≤106	O（nlogn ）或O（n）
n 很大	O（1）或O（log n）

请记住，时间复杂度是一个近似值，而不是保证。我们可以通过立即排除不太可能满足约束条件的算法设计来节省大量时间和精力，但我们也必须考虑到大 O 符号不考虑常数因子。以下是一些代码来说明。

以下两个算法都具有O（n）时间复杂度。

func makeCoffee(scoops int) {
    for scoop := 0; scoop <= scoops; scoop++ {
        // add instant coffee
    }
}

func makeStrongCoffee(scoops int) {
    for scoop := 0; scoop <= 3*scoops; scoop++ {
        // add instant coffee
    }
}

第一个函数制作一杯咖啡，其数量与我们请求的勺数相同。第二个函数同样制作一杯咖啡，但其勺数是请求数量的三倍。为了看一个示例，我们让这两个函数都制作一杯包含一百万勺的咖啡。

以下是 Go 测试的输出：

Benchmark_makeCoffee-4          1000000000               0.29 ns/op
Benchmark_makeStrongCoffee-4    1000000000               0.86 ns/op

我们的第一个函数makeCoffee平均耗时 0.29 纳秒。第二个函数makeStrongCoffee平均耗时 0.86 纳秒。虽然这两个数字看起来都很小，但考虑到更浓的咖啡制作时间几乎是后者的三倍。这直观上应该说得通，因为我们要求它将勺数增加三倍。单凭大 O 符号无法告诉你这一点，因为三倍勺数的常数因子没有被考虑进去。

提高现有代码的时间复杂度

熟悉时间复杂度让我们有机会编写代码或重构代码，从而提高效率。为了说明这一点，我将举一个具体的例子，说明如何重构一段代码来提高其时间复杂度。

假设办公室里有一群人想吃馅饼。有些人比其他人更想吃馅饼。每个人想要馅饼的数量可以用一个int> 0的数来表示：

diners := []int{2, 88, 87, 16, 42, 10, 34, 1, 43, 56}

可惜我们资金不足，只有三把叉子。既然我们是一群合作的人，那么最想吃馅饼的三个人就能拿到叉子吃。虽然大家都同意了，但似乎没人想理清头绪，排成整齐的队，所以我们只好凑合着吃，大家都乱成一团。

不对用餐者列表进行排序，返回切片中最大的三个整数。

下面是一个可以解决这个问题的函数，其时间复杂度为O ( n2 ^{) ：}

func giveForks(diners []int) []int {
    // make a slice to store diners who will receive forks
    var withForks []int
    // loop over three forks
    for i := 1; i <= 3; i++ {
        // variables to keep track of the highest integer and where it is
        var max, maxIndex int
        // loop over the diners slice
        for n := range diners {
            // if this integer is higher than max, update max and maxIndex
            if diners[n] > max {
                max = diners[n]
                maxIndex = n
            }
        }
        // remove the highest integer from the diners slice for the next loop
        diners = append(diners[:maxIndex], diners[maxIndex+1:]...)
        // keep track of who gets a fork
        withForks = append(withForks, max)
    }
    return withForks
}

这个程序运行正常，最终返回了 diners [88 87 56]。不过，程序运行时大家有点不耐烦，因为光是分发三把叉子就花了相当长的时间（大约 120 纳秒），而且馅饼也快凉了。我们该如何改进它呢？

通过稍微不同的方式思考我们的方法，我们可以重构这个程序，使其具有O ( n ) 时间复杂度：

func giveForks(diners []int) []int {
    // make a slice to store diners who will receive forks
    var withForks []int
    // create variables for each fork
    var first, second, third int
    // loop over the diners
    for i := range diners {
        // assign the forks
        if diners[i] > first {
            third = second
            second = first
            first = diners[i]
        } else if diners[i] > second {
            third = second
            second = diners[i]
        } else if diners[i] > third {
            third = diners[i]
        }
    }
    // list the final result of who gets a fork
    withForks = append(withForks, first, second, third)
    return withForks
}

新程序的运作方式如下：

最初，diner 2（列表中的第一个）被分配了first餐叉。其他餐叉保持未分配状态。

然后，88第一个叉子就被分配给了diner。Diner2拿到了那second把。

Diner87并不大于first当前的 which 88，但它大于2who has the secondfork 。因此，second叉子归87。Diner2拿到了third叉子。

继续这种激烈而快速的叉子交换，用餐者16就会得到third叉子而不是2，依此类推。

我们可以在循环中添加一个打印语句来查看 fork 分配如何进行：

这个程序的速度要快得多，整个争夺叉子统治权的史诗般的斗争在 47 纳秒内就结束了。

正如您所见，通过一些视角的改变和重构，我们使这段简单的代码变得更快、更高效。

好了，看来我们的十五分钟咖啡休息时间到了！希望我已经全面地介绍了时间复杂度的计算方法。该回去工作了，希望你能运用新学到的知识编写出更高效的代码！或者，下次办公室聚会时，也能展现你的聪明才智。:)

来源

“如果我看得更远，那是因为我站在巨人的肩膀上。”——艾萨克·牛顿，1675年

安蒂·拉克索宁程序员竞争手册 (pdf)， 2017
维基百科：大 O 符号
StackOverflow：如何用简单的英语解释“大 O”符号？
维基百科：多项式
维基百科：NP 完全性
维基百科：NP硬度
Desmos 图形计算器

感谢阅读！如果您觉得这篇文章有用，请分享给其他可能受益的人！

您可以在Victoria.dev上找到此帖子和其他解释使用有趣涂鸦进行编码的帖子。

文章来源：https://dev.to/victoria/a-coffee-break-introduction-to-time-complexity-of-algorithms-160m

咖啡时间介绍算法的时间复杂度 什么是“时间复杂度”？确定时间复杂度 P vs NP、NP-complete 和 NP-hard 在编写代码之前估算算法的效率 改进现有代码的时间复杂度 资料来源

咖啡休息时间介绍算法的时间复杂度

那么“时间复杂度”到底是什么呢？

确定时间复杂度

P 与 NP、NP 完全问题和 NP 难问题

在编写代码之前估算算法的效率

提高现有代码的时间复杂度

来源

那么“时间复杂度”到底是什么呢？

确定时间复杂度

多项式时间复杂度

持续的

线性

二次函数

立方体

对数

准线性

非多项式时间复杂度

阶乘

指数

递归时间复杂度

最坏情况时间复杂度

P 与 NP、NP 完全问题和 NP 难问题

在编写代码之前估算算法的效率

提高现有代码的时间复杂度

来源

咖啡时间介绍算法的时间复杂度什么是“时间复杂度”？确定时间复杂度 P vs NP、NP-complete 和 NP-hard 在编写代码之前估算算法的效率改进现有代码的时间复杂度资料来源