使用 Javascript 的简单英语综合大 O 符号指南

如果您是计算机科学专业的学生或毕业生，那么可以 100% 肯定地认为这是您绝对了解的一个主题。

但是，如果你目前正在自学编程，或者像我一样已经是自学成才的程序员，你可能根本没听说过这个术语。但我向你保证，你迟早都会遇到这个问题。当你遇到它时，一开始可能会感到害怕。说实话，我也曾感到害怕——直到我决定深入了解它。

摘自维基百科页面：https://en.wikipedia.org/wiki/Big_O_notation

大 O 符号是一种数学符号，用于描述函数在参数趋向于特定值或无穷大时极限行为。大 O 符号属于保罗·巴赫曼[1]、埃德蒙·兰道[2]等人发明的一系列符号，统称为巴赫曼-兰道符号或渐近符号。

在计算机科学中，大 O 符号用于根据算法的运行时间或空间需求随输入规模增长而增长的方式对其进行分类。[3] 在解析数论中，大 O 符号常用于表示算术函数与其更易于理解的近似值之间差异的界限；一个著名的例子是素数定理中的余项。大 O 符号也用于许多其他领域，以提供类似的估计。

这段描述对你来说容易理解和记住吗？虽然它是正确的，但我一开始并不容易理解。让我和你分享一下我理解它的方式——我希望你也能理解。

那么，什么是大 O 符号以及我们为什么需要它？

简单来说，大 O 符号用于衡量我们编写的函数或算法的性能和可扩展性。本质上，它是一种数学符号，正如维基百科文章中提到的那样——但您无需精通数学即可使用它。

你可能会问，既然有工具可以显示运行一段代码需要多少毫秒，为什么还要用大 O 呢？虽然它很方便，但对于可靠的分析来说，它仍然不够一致。因为如果你的电脑比我的强，我们代码的执行时间就不会一样。即使在同一台电脑上，执行时间也会根据当时 CPU 和 RAM 的性能而变化。有了大 O，我们就不必担心所有这些细节了。

当我们谈论可扩展性时，我们指的是随着输入量的增长，函数或算法的速度会降低多少。假设你有一个包含 100 个用户的应用程序。你使用一个函数循环遍历 100 个用户的列表以获取他们的姓名。该函数将在几毫秒内完成这项工作。

但是，当你的应用程序规模不断扩大，需要处理 1 万、10 万甚至数百万用户时，会发生什么情况呢？我们该如何找到一种数据结构和算法来有效地解决这个问题呢？这时，大 O 符号就能派上用场了。

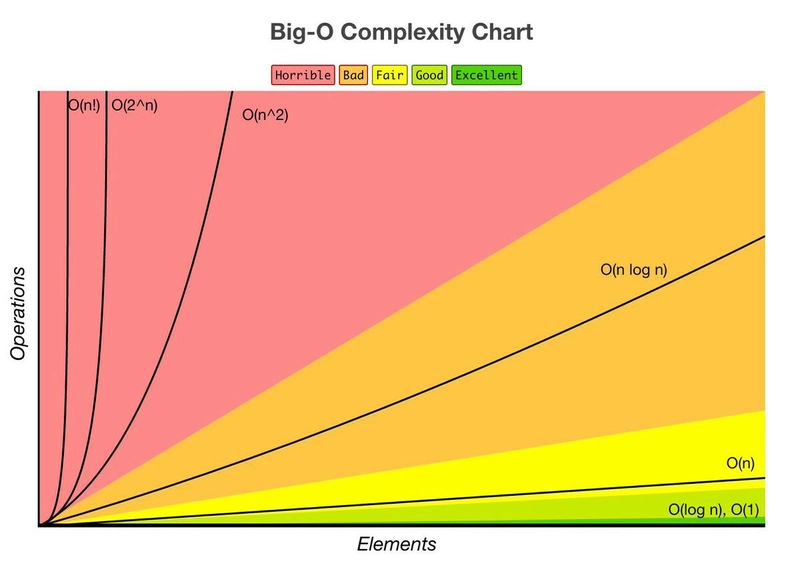
理解 Big O 复杂度图

- 图表来源：https://www.bigocheatsheet.com/ -

这张图非常直观地展示了使用区域颜色进行缩放的优缺点。但为了让你更好地理解这张图，我可以分享一个演示此代码的交互式 gif 动图：

const example = [1, 2, 3, 4, 5, 6, 7]

function printArray (arr) {
  for (let i = 0; i < arr.length; i++) {
    console.log('element:', arr[i])
  }
}

printArray(example)

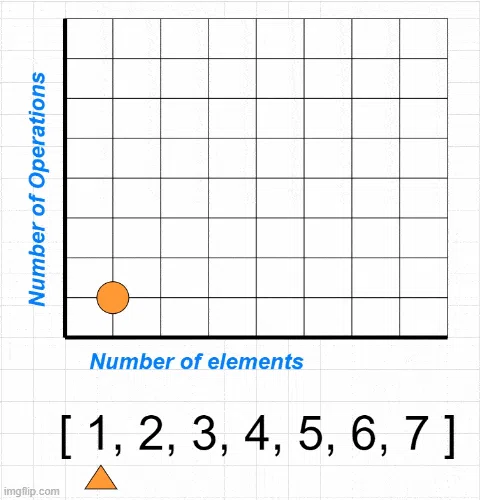
在代码中，我们只是循环遍历一个数字数组，并在控制台上打印每个值。正如下面的 gif 图所示，操作次数会随着数组的大小而增加——因为在这段代码中，我们对每个元素执行一次操作：

时间和空间复杂度

我们使用 Big O 来分析算法的时间和空间复杂度。时间和空间是编写高效代码的两个重要指标。

时间复杂度：它与速度有关——运行算法需要多长时间。速度取决于CPU (Central Processing Unit)计算机的性能。

空间复杂度：它与内存有关——运行算法需要多少内存。这里的内存是指算法需要使用的临时内存空间，称为辅助空间。内存大小取决于RAM (Random Access Memory)计算机的内存容量。

如今，我们拥有强大的计算机，但我们的资源仍然不是无限的。

因此，当您下次听到时间和空间复杂性时，请记住这一点：这是关于明智地使用资源。

如果您正在解决编程问题，那么时间和空间之间就会存在权衡。

当您希望某些东西运行得更快时，您可能必须为此牺牲更多的内存。

当你想让某些东西在内存中更便宜时，你可能不得不接受较低的速度。

这是一种平衡的行为——不同的设备、软件或平台需要不同类型的时间和空间平衡。作为一名程序员，掌握这些知识将有助于你更有效地解决问题。

我相信到目前为止，我们对大 O、时间和空间复杂度的定义以及我们为什么需要它们已经有了很好的理解。让我们继续熟悉最常见的大 O 符号。

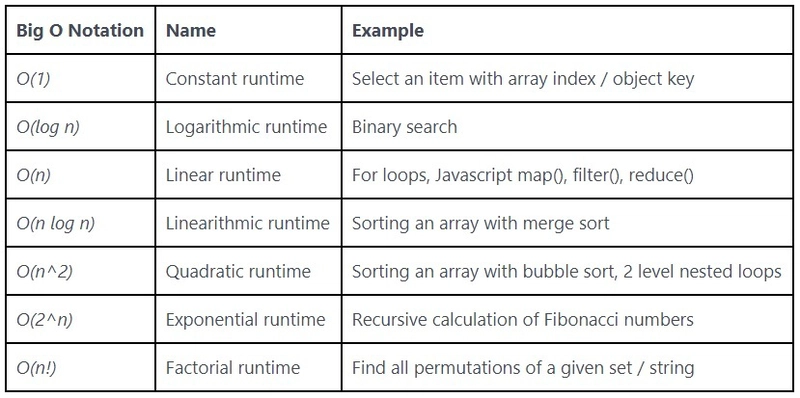
以下是我们将要讨论的复杂问题列表：

在我开始解释之前，我猜你一定想知道O和括号内的数字或符号（如(n)）代表什么。

O表示函数的阶数

（n）表示输入的数量

O（1）-恒定时间

复杂度等级：优秀

在扩展性方面，恒定时间是最优的复杂度。为什么？因为顾名思义，它是恒定的：无论需要操作多少项，运行算法所需的时间都是完全相同的。

const tenItems = new Array(10).fill('foo')
const millionItems = new Array(1000000).fill('bar')

function returnFirstElement (arr) {
  return arr[0]
}

returnFirstElement(tenItems)
// this will take same amount of time as tenItems array:
returnFirstElement(millionItems)

看到了吗？在这种情况下，元素数量无关紧要。我们取第一个元素就完成了。但请记住，恒定时间不仅仅是只选择一个元素。可以这样想：无论有多少个输入，我们执行的操作数量都不会改变——因为它与输入的大小无关。看看这个例子：

const tenItems = new Array(10).fill('foo')
const millionItems = new Array(1000000).fill('bar')

function printOnlyFirstFive (array) {
 for (i = 0; i < 5; i++) {
   console.log('element:', array[i])
 }
}

printOnlyFirstFive(tenItems)
// this will take same amount of time as tenItems array:
printOnlyFirstFive(millionItems)

现在你可能会想，在第一个例子中，我们只对一个元素进行了操作，所以它是O(1)。O(5)那么我们可以这样称呼它吗？是的，你可以将常量的数量算作O(5)- 但最终它仍然是常量。按照命名约定，我们将其称为O(1)或常数时间。

通过对象的键获取值也是恒定运行时的一个例子。无论对象有多少个元素，获取值的时间都是恒定的：

const todaysMenu = {
  breakfast: 'Smoothie',
  lunch: 'Sallad',
  dinner: 'Sushi',
};

function whatIsInTheMenu(menu, type) {
  return menu[type]
}

whatIsInTheMenu(todaysMenu, 'breakfast') // => Smoothie

如下函数也是恒定运行时算法的一个例子。无论数字有多大，它们都遵循一个恒定的模式：

function addTen(n) {
  return n + 10
}

console.log(addTen(10)); // => 20
console.log(addTen(1000000)); // => 1000010


function isEvenOrOdd(n) {
  return n % 2 ? 'Odd' : 'Even';
}


console.log(isEvenOrOdd(10)); // => Even
console.log(isEvenOrOdd(10001)); // => Odd

恒定运行时算法的一些示例：

从具有索引号的数组中选择一个元素。
从具有键值的对象中选择一个元素。
检查数组中的某个项目是否为空。

一些具有恒定时间复杂度的内置 Javascript 方法：

数组： push()、pop()

请记住：诸如求和、乘法、减法、除法、模数、位移等基本数学运算也具有恒定的运行时间。

O（log n）——对数时间

复杂度等级：良好

对数运行时间算法是规模上仅次于常数运行时间算法的算法，速度仅次于常数运行时间算法。最简洁的解释是：对数运行时间通常适用于每一步将问题一分为二的算法。

一个很好的类比是想象一下你在字典里搜索单词的方式。比如，你想查找“tree”这个词。你不会从头开始逐页翻开来搜索。相反，你会把书页翻开，直接随机翻到最接近“T”部分的一页。如果你翻得太远，比如说“U”部分——你只会尝试回到“T”部分，而不会回到它之前的部分。

对数运行时间的典型示例是二分查找。二分查找是一种通过在每次迭代中将输入除以二来查找参数在已排序数组中位置的算法。我特别强调了“sorted”，因为数组必须经过排序才能通过该算法获得准确的结果。当你需要使用二分查找时，请记住这一点。

假设我们有一个包含 10 个元素的数组，我们想找到值为 5 的元素。首先要做什么？用 for 循环，对吧？在这种情况下，这也可以称为暴力破解：我们只需使用 for 循环（线性搜索）迭代数组即可：

const tenArray = Array.from(Array(10).keys())

const linearSearch = (arr, target) => {
   for (let i = 0; i < arr.length; i++) {
       if (arr[i] === target) {
           return `Found the target: ${target} at index ${i}`;
       }
   }
}

linearSearch(tenArray, 5)

这将花费O(n) - Linear runtime您查找元素的时间。您将在下一章中了解有关此运行时间的更多详细信息 - 但为了便于示例，我将在下面向您展示，只需知道线性运行时间直接取决于输入的长度。请这样思考：搜索 100 个输入所需的时间是搜索 10 个项目的 10 倍。

现在，让我向你演示一下线性搜索和二分搜索之间的规模差异。我将使用 JavaScript 的性能 API 进行粗略的比较。我也鼓励你复制粘贴这些代码片段，并在你最喜欢的代码编辑器中尝试一下。

再次强调，正如我之前提到的，这些数字会根据你的电脑性能而有所不同。即使是同一台电脑，根据当时电脑的性能，数字也会有所不同。如果你得到的数字与我这里得到的并不完全相同，也不用担心，我们关注的只是不同运行时的扩展差异。

const tenArray = Array.from(Array(10).keys())

// O(n) - LINEAR RUNTIME
const linearSearch = (arr, target) => {
   for (let i = 0; i < arr.length; i++) {
       if (arr[i] === target) {
           return `Found the target: ${target} at index ${i}`;
       }
   }
}

// O(log n) - LOGARITHMIC RUNTIME
const binarySearch = (arr, target) => {
   let startIndex = 0;
   let endIndex = (arr.length)-1;

   while (startIndex <= endIndex){

       let pivot = Math.floor((startIndex + endIndex)/2);

       if (arr[pivot] === target) {
            return `Found the target: ${target} at index ${pivot}`;
       } else if (arr[pivot] < target) {
           startIndex = pivot + 1;
       } else {
           endIndex = pivot - 1;
       }
   }
   return false;
}

let beforeLinear = performance.now()
linearSearch(tenArray, 5)
let afterLinear = performance.now()

let beforeBinary = performance.now()
binarySearch(tenArray, 5)
let afterBinary = performance.now()

console.log('Milliseconds linear search:', afterLinear - beforeLinear)
console.log('Milliseconds binary search:', afterBinary - beforeBinary)

// RESULT:
// => 'Milliseconds linear search:' 0.02500019036233425
// => 'Milliseconds binary search:' 0.06500002928078175

如示例所示，我们迭代了 10 个元素。线性算法的执行速度比对数算法快 2.6 倍。现在，让我们看看当迭代 100 万个项目时，算法的扩展性如何：

const millionArray = Array.from(Array(1000000).keys())

// O(n) - LINEAR RUNTIME
const linearSearch = (arr, target) => {
   for (let i = 0; i < arr.length; i++) {
       if (arr[i] === target) {
           return `Found the target: ${target} at index ${i}`;
       }
   }
}

// O(log n) - LOGARITHMIC RUNTIME
const binarySearch = (arr, target) => {
   let startIndex = 0;
   let endIndex = (arr.length)-1;

   while (startIndex <= endIndex){

       let pivot = Math.floor((startIndex + endIndex)/2);

       if (arr[pivot] === target) {
            return `Found the target: ${target} at index ${pivot}`;
       } else if (arr[pivot] < target) {
           startIndex = pivot + 1;
       } else {
           endIndex = pivot - 1;
       }
   }
   return false;
}

let beforeLinear = performance.now()
linearSearch(millionArray, 567841)
let afterLinear = performance.now()

let beforeBinary = performance.now()
binarySearch(millionArray, 567841)
let afterBinary = performance.now()

console.log('Milliseconds linear search:', afterLinear - beforeLinear)
console.log('Milliseconds binary search:', afterBinary - beforeBinary)

// RESULT:
// => 'Milliseconds linear search:' 2.185000106692314
// => 'Milliseconds binary search:' 0.054999953135848045

现在，差异非常显著。当我们迭代 100 万个项目时，二分查找的速度比线性查找快 40 倍！但当我们对 10 个项目使用完全相同的函数时，线性查找的速度比二分查找快 2.6 倍。我相信这是一个很好的例子，展示了通过为要解决的问题选择正确的算法，可以对性能产生多大的差异。

O（n）-线性时间

复杂度等级：一般

我们说的线性时间到底是什么意思？如果我告诉你，我们知道的所有循环都是线性时间复杂度/增长的例子，你或许会更容易理解。

因为循环完成的时间与数组的长度直接相关。迭代 100 个元素所需的时间是迭代 10 个元素的 10 倍。

const tenItems = new Array(10).fill('foo')
const hundredItems = new Array(100).fill('bar')

function printArray (arr) {
  for (let i = 0; i < arr.length; i++) {
    console.log('element:', arr[i])
  }
}

printArray(tenItems)
// this will take 10 times longer than iterating tenItems array:
printArray(hundredItems)

线性运行时算法的一些示例：

打印列表中的所有值。
在集合中查找给定元素。
获取数组中的最大值或最小值。

一些具有线性时间复杂度的内置 Javascript 方法：

数组： shift()、unshift()、splice()、concat()、slice()、indexOf()、forEach()、map()、filter()、reduce()

O(n log n) - 线性对数时间

复杂度等级：接近公平

线性时间复杂度比线性算法稍慢 - 但仍然比二次算法（您将在下一节中看到）更好。O(n log n)经常与混淆。它是线性和对数运行时复杂度O(log n)的组合。O(n)O (log n)

它们如何结合起来？首先n是线性时间复杂度，乘以log n

O(n * log n)->O (n log n)

采用分而治之策略的排序算法是线性对数的，例如：

归并排序、快速排序、堆排序、Timsort

我们来看一个例子，合并排序：

const someArray = [ 3, 14, 7, 11, 6, 1, 21, 9, 14, 15 ]

// sorting helper:
const merge = (left, right) => {
    let result = [];

    while(left.length || right.length) {

        if(left.length && right.length) {
            if(left[0] < right[0]) {
                result.push(left.shift())
            } else {
                result.push(right.shift())
            }
        } else if(left.length) {
            result.push(left.shift())
        } else {
            result.push(right.shift())
        }
    }
    return result
}

// main function
const mergeSort = (arr) =>{
    if(arr.length <= 1) {
        return arr
    }

    const pivot = arr.length / 2
    const left = arr.slice(0, pivot)
    const right = arr.slice(pivot, arr.length)

  return merge(mergeSort(left), mergeSort(right))
};

mergeSort(someArray)

我不会在这里对归并排序进行详细的分析，但让我用简单的英语给你一个简单的概述 - 这样我们就可以看看它的大 O 方面。

归并排序的工作原理如下：

- 它接受未排序的数组。

- 一步一步地将数组分成更小的部分。

- 对它们进行排序。

- 然后将它们合并回去，构建一个完全排序的数组。

- 为此，它递归地使用merge()我们在代码块中看到的方法。递归是什么意思？简而言之，它是一个函数调用自身，直到满足某个条件。它通常被称为退出条件。如上所示，退出条件基于数组长度。

从 Big O 角度来看，我们看到了什么：

merge()-> 此方法的时间复杂度基于数组长度，因此它是线性运行时间O(n)

mergeSort()-> 每次迭代时，它会将数组分成两部分。还记得我们讨论过的二分查找吗？归并排序在这里以类似的方式工作，每次迭代时，左右数组都会减半。因此，对数运行时间O(log n)也存在。

最后，当我们合并这两个函数时，我们得到 ->O(n log n)

O(n^2) - 二次时间

复杂度等级：差

二次方是描述平方（或2 的幂）的名称。它实际上就是数学中数字的平方。

快速复习：一个数的平方是什么？一个数的平方等于该数乘以自身。

2 的 2 次方，即，与，或 42^2相同。2 * 2

5 的 2 次方，即 5^2，与，或 25 相同 5 * 5。

二次运行时最经典的例子是使用相同数组的嵌套循环。因为你正在一个线性运行时操作中运行另一个线性运行时操作 ->O(n * n) = O(n ^ 2)

让我们看一个例子：

const fruits = ["apple", "strawberry", "watermelon"]

function logAllPairs(arr) {
  for (i = 0; i < arr.length; i++) {
    for (j = 0; j < arr.length; j++) {
      console.log(`${arr[i]} - ${arr[j]}`)
    }
  }
}

logAllPairs(fruits)

/* Output => 
'apple - apple'
'apple - strawberry'
'apple - watermelon'
'strawberry - apple'
'strawberry - strawberry'
'strawberry - watermelon'
'watermelon - apple'
'watermelon - strawberry'
'watermelon - watermelon'
*/

这里，我们使用同一个数组来打印所有对。如你所见，为了从 3 个元素长度的数组中获取结果，我们需要运行 9 次：

3 * 3或者3 to the power of 2。

如果我们使用 3 个嵌套循环会发生什么？它还能被称为二次运行时吗？不能。它将被称为三次运行时，因为我们将拥有O (n ^ 3)或O (n * n * n)

为了更好地理解，具有二次、三次或类似运行时间的函数也称为多项式时间复杂度。也可以表示为：O(n ^ k)

n - 输入

k - (2、3、... 任意) 的幂

请记住：k值越大，算法越慢。三次算法的运行时间会比二次算法慢得多。

O（2^n）——指数时间

复杂度等级：糟糕

指数或以 2 为底意味着算法执行的计算量随着输入的增加而每次翻倍。我们也可以说这与对数运行时间相反O(log n)——因为每一步计算量都会减少一半，而指数运行时间则会翻倍。指数运行时间的典型示例是递归计算斐波那契数列。让我简单介绍一下：

- 斐波那契数是从 0 开始的前 2 个邻居数之和。

- 请记住 - 实际计算从第三个索引开始（或者如果我们从索引 [0] 开始计算数组，我们可以说索引 [2]）。因为它是第一个具有两个先前邻居的索引：

- 使用以下函数，我们将给出一个索引号，以便使用递归返回序列中的第 n个斐波那契数列。此解决方案也称为此问题的“简单”解决方案，我建议您查看并研究用于查找斐波那契数列的优化解决方案。目前，我们只想关注大 O 方面：

function fibonacciRecursive(num) {
  // exit conditions, return if it is 0 or 1
  if (num === 0) return 0
  else if (num === 1) return 1
  // else, call the function recursively
  else return fibonacciRecursive(num - 1) + fibonacciRecursive(num - 2)
}

fibonacciRecursive(4)
// OUTPUT => 3

这里发生了什么？当我们运行该函数时，我们得到了多个返回的递归结果。每一步计算量都会翻倍！

fibonacciRecursive(4) = fibonacciRecursive(3) + fibonacciRecursive(2)
fibonacciRecursive(3) = fibonacciRecursive(2) + fibonacciRecursive(1)
fibonacciRecursive(2) = fibonacciRecursive(1) + fibonacciRecursive(0) 
// fib(1) and fib(0) are 0 and 1 respectively

从堆栈中弹出：

fibonacciRecursive(2) = 1 + 0 = 1
fibonacciRecursive(3) = 1 + 1 = 2
fibonacciRecursive(4) = 1 + 2 = 3

时间复杂度增长非常快。瞧，我们调用了fibonacci(2)和fibonacci(1)两次。

如果可能的话，你应该避免使用指数级运行时间的函数，因为它们的扩展性很糟糕。但这还不是最糟糕的。还有一个时间复杂度的问题，我们需要在下一节讨论。

O（n！）-阶乘时间

复杂性排名：最差

阶乘是一个数字，它是该数字以下所有正整数相乘的结果。

6! = 6 x 5 x 4 x 3 x 2 x 1 = 720

看到了吗？它长得非常快。

阶乘运行时的经典应用示例是旅行商问题。假设你是一名销售人员，需要访问n个城市。那么，哪条路线能让你访问每个城市，然后返回出发地？为了解决这个问题，我们需要计算所有可能的路线。这时，排列就派上用场了。

本周你需要访问3个城市。有多少种排列组合？

function getPermutations (arr) {
  if (arr.length <= 2) {
    if (arr.length === 2) return [arr, [arr[1], arr[0]]]
    return arr
  }
  return arr.reduce(
    (acc, item, i) =>
      acc.concat(
        getPermutations([...arr.slice(0, i), ...arr.slice(i + 1)]).map(val => [
          item,
          ...val,
        ])
      ),
    []
  );
}

const cities = ['Copenhagen','Stockholm', 'Oslo']
getPermutations(cities)

这是阶乘 3，即3!，返回 6 条不同的路线：

[
  [ 'Copenhagen', 'Stockholm', 'Oslo' ],
  [ 'Copenhagen', 'Oslo', 'Stockholm' ],
  [ 'Stockholm', 'Copenhagen', 'Oslo' ],
  [ 'Stockholm', 'Oslo', 'Copenhagen' ],
  [ 'Oslo', 'Copenhagen', 'Stockholm' ],
  [ 'Oslo', 'Stockholm', 'Copenhagen' ]
]

如果你需要计算18个城市的排列组合，会发生什么？答案是18！阶乘。

将会有6,402,373,705,728,000 条不同的路线！

如果可能的话，你应该避免使用这种运行时间的算法。为了优化这类问题，我建议你研究一下启发式算法。

希望本文能帮助您理解 Big O Notation 的概念，并让您熟悉常见的 Big O 运行时复杂性。感谢您的阅读！

文章来源：https://dev.to/humblecoder00/compressive-big-o-notation-guide-in-plain-english-using-javascript-3n6m