使用 Minimax 算法进行井字游戏

在本文中，我想展示一个使用极小极大算法实现的井字棋解算器。由于井字棋游戏简单，状态相对较少，我认为它很适合作为机器学习和人工智能实验的一个案例研究。在这里，我实现了一个名为极小极大算法的简单算法。

极小极大背后的基本思想是，当我们假设对手会做出最佳举动时，我们想知道该如何出牌。例如，假设轮到X出牌，X采取特定的举动。这一举动的价值是多少？假设O可以用以下两种方式之一应对：在第一种情况下，O在下一步行动中获胜。O 的另一步行动导致X在下一步行动中获胜。由于O可以获胜，我们认为X的原始举动是错误的 — — 它会导致失败。我们忽略如果O犯错X可能会获胜的事实。我们将定义X获胜的值设为1，O获胜的值设为-1，平局的值设为0。在上述情况下，由于O可以在下一步行动中获胜，因此X的原始举动被赋予-1的值。

极小最大算法从任何给定位置递归应用此策略 - 我们从给定的起始位置探索游戏，直到达到所有可能的游戏结束状态。我们可以将其表示为一棵树，树的每一层都显示给定玩家回合的可能棋盘位置。当我们到达游戏结束状态时，没有选择，因此值是游戏结果，即如果X赢了则为1，如果O赢了则为-1 ，如果平局则为0。如果轮到X并且不是最终棋盘状态，则我们选择树中该位置的下一个可能移动的值中的最大值。这代表了X的最佳选择。如果轮到O了，那么我们选择这些值中的最小值，这是O的最佳选择。我们继续将位置值向上传播到根位置，在此过程中在最大值和最小值之间交替 - 这当然是极小最大算法名称的由来。

下图展示了极小极大策略应用于棋盘位置的示例：

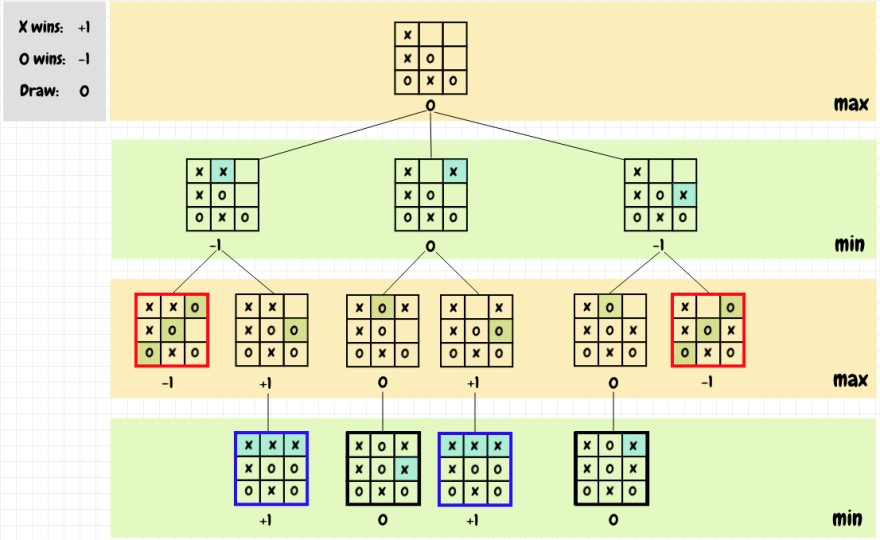
如果该位置是游戏结束状态，那么该位置的值就是该游戏的结果——这是递归调用的终止条件。一旦我们到达游戏结束位置，我们就可以向上返回根位置。对于树的最大层级（轮到X了）的位置，我们从可能的延续中选择具有最大值的移动。对于树的最小层级（轮到O了）的位置，我们取最小值。在每种情况下，我们都在寻找当前玩家下一步行动的最佳结果。如我们所见，图中X所能做的最好的事情（只要O没有犯错）是在棋盘的右上角下棋以获得平局。

值得强调的是，对于像井字游戏这样的玩具场景，极小极大算法效果很好：游戏位置很少 - 如果考虑旋转和反射对称，则有765 种。对于更复杂的场景，包括国际象棋和围棋这样的游戏，极小极大算法至少必须与其他技术相结合。我在这里没有实现它，但是可以使用alpha-beta 剪枝来减少需要访问的位置数。总体思路是，如果我们知道探索子树不会产生比我们已经得到的结果更好的结果，那么我们就不需要为此烦恼。还有其他启发式方法。我们可以限制搜索深度，一旦达到该限制，我们可以使用启发式方法来估计位置的可能值。这个想法已经在像Stockfish这样的国际象棋引擎中得到了广泛的应用。MCTS是另一种技术，可用于简化极小极大算法会导致太多组合而无法跟踪的场景。如今，深度学习已被证明在国际象棋和围棋等游戏中非常有效。事实上，它比任何其他已知技术都有效得多。

让我们简要看一下实现极小化极大算法所需的代码。请注意，此代码并非为了追求最高效率而编写，仅用于说明基本概念。该项目可在GitHub上找到。以下代码来自以下minimax.py文件：

def play_minimax_move(board):
    move_value_pairs = get_move_value_pairs(board)
    move = filter_best_move(board, move_value_pairs)

    return play_move(board, move)

play_minimax_move确定在给定棋盘位置下哪一步棋。首先，它获取每个可能走法对应的值，然后如果轮到X走，则走具有最大值的一步棋；如果轮到O走，则走具有最小值的一步棋。

get_move_value_pairs从当前棋盘位置获取下一步动作的值：

def get_move_value_pairs(board):
    valid_move_indexes = get_valid_move_indexes(board)

    assert not_empty(valid_move_indexes), "never call with an end-position"

    move_value_pairs = [(m, get_position_value(play_move(board, m)))
                        for m in valid_move_indexes]

    return move_value_pairs

get_position_value下面的这个方法要么从缓存中获取当前位置的值，要么直接通过探索博弈树来计算。如果没有缓存，在我的电脑上玩一局游戏大约需要 1.5 分钟。缓存可以将时间缩短到大约 0.3 秒！完整的搜索会多次遇到相同的位置。缓存可以显著加快这个过程：如果我们之前见过某个位置，就不需要重新探索博弈树的那部分。

def get_position_value(board):
    cached_position_value, found = get_position_value_from_cache(board)
    if found:
        return cached_position_value

    position_value = calculate_position_value(board)

    put_position_value_in_cache(board, position_value)

    return position_value

calculate_position_value当给定棋盘的值尚未存在于缓存中时，查找该值。如果游戏已结束，我们将游戏结果作为该位置的值返回。否则，我们将递归地回调到，get_position_value并处理每个有效的可能走法。然后，根据轮到谁了，我们要么获取所有这些值的最小值，要么获取最大值：

def calculate_position_value(board):
    if is_gameover(board):
        return get_game_result(board)

    valid_move_indexes = get_valid_move_indexes(board)

    values = [get_position_value(play_move(board, m))
              for m in valid_move_indexes]

    min_or_max = choose_min_or_max_for_comparison(board)
    position_value = min_or_max(values)

    return position_value

我们可以看到，如果轮到O 了，或者轮到Xchoose_min_or_max_for_comparison了，则返回函数：minmax

def choose_min_or_max_for_comparison(board):
    turn = get_turn(board)
    return min if turn == CELL_O else max

回到缓存问题，缓存代码还会考虑等效位置，包括旋转以及水平和垂直反射。旋转时有 4 个等效位置：0°、90°、180° 和 270°。此外，还有 4 种反射：水平和垂直翻转原始位置，以及先旋转 90°，然后水平和垂直翻转。其余旋转的翻转是多余的：翻转 180° 旋转将产生与翻转原始位置相同的位置；翻转 270° 旋转将产生与翻转 90° 旋转相同的位置。如果不考虑旋转和反射，在我的电脑上，单局游戏大约需要 0.8 秒，而启用旋转和反射缓存时则需要 0.3 秒。get_symmetrical_board_orientations获取所有等效棋盘位置，以便在缓存中查找它们：

def get_symmetrical_board_orientations(board_2d):
    orientations = [board_2d]

    current_board_2d = board_2d
    for i in range(3):
        current_board_2d = np.rot90(current_board_2d)
        orientations.append(current_board_2d)

    orientations.append(np.flipud(board_2d))
    orientations.append(np.fliplr(board_2d))

    orientations.append(np.flipud(np.rot90(board_2d)))
    orientations.append(np.fliplr(np.rot90(board_2d)))

    return orientations