大 O 符号 - 简介

你可能想知道为什么我加了一张蓝色外星人的照片作为封面图。它是我最喜欢的电影之一《家园》里的角色，他的名字叫 Oh。Oh，就像大写的“Oh”符号一样。明白了吗😂？
现在我们开始认真起来吧。

很久以前，在 10 倍速工程师出现之前，软件工程师们就一直在探索如何运用他们的编程技能来解决实际问题。不同的工程师提出了不同的解决方案/算法来解决这些问题。他们需要根据这些解决方案的复杂性和效率进行比较。这种需求催生了“大 O 符号”。那么，“大 O 符号”究竟是什么呢？

什么是大 O 符号？

大 O 符号在计算机科学中用于描述算法的性能或复杂性。

算法之于计算机程序，就如同菜谱之于菜肴。不同的菜谱可以帮你做出特定的菜肴，但它们并不总是能做出相同的结果。它们的步骤、食材和时间并不总是相同的。有些菜谱比其他菜谱更快，效果也更好。

同样，不同的算法可以实现特定的计算机程序。然而，它们的效率和运行时间并不相同。我们使用“大O”来衡量算法的效率。

例如，我们来考虑排序。排序算法有很多种，例如归并排序、冒泡排序、快速排序和插入排序。如何知道哪种算法更高效、更简单呢？这就是大 O 符号存在的原因。

你可能会想，为什么我们需要一个符号？为什么不直接考虑运行算法所需的时间呢？以下是其中两个原因：

不同的计算机有不同的处理器，因此有些计算机运行算法所花的时间比其他计算机少。
有些编程语言比其他编程语言更快。

在尝试分析算法时，考虑所有这些因素会让人感到压力很大。大 O 符号并非如此，而是使用更标准的东西——输入。它考虑了算法的运行时间如何随着输入的大小而增长。值得注意的是，大 O 符号在分析时考虑了最坏情况。

希望你现在明白了。接下来你可能会想：“我为什么要知道这个？”

你为什么要关心？

对于处理少量数据的小型应用来说，这种分析可能没有必要。这是因为算法运行时的差异可能对您的应用影响不大。对于处理大量数据的大型应用来说，这种分析至关重要。因为低效的算法会对处理时间产生显著影响。掌握大O符号，您就可以设计高效的算法。这样，您将构建可扩展的应用，并避免许多潜在的麻烦。
对于你的编程面试来说。是的，你没听错。面试官很可能会问你解决方案的运行时复杂度。所以了解一下大 O 符号是很有好处的。

让我们看一些 Big O 符号的常见例子

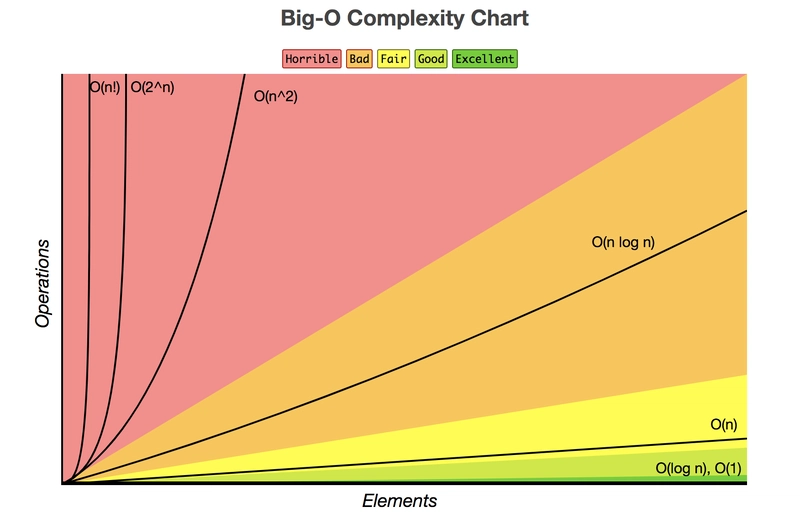
常见的运行时复杂性

1. O(1) - 恒定运行时间

在这种情况下，无论给定的输入数据集如何，您的算法运行时间都相同。

一个例子是返回给定数据中的第一个元素，如下例所示。

function returnFirst(elements) {
   return elements[0]
}

无论给定的输入大小如何，运行时间都是恒定的。

2. O（n） - 线性运行时间

当运行时间与输入数据集的大小成比例增长时，就会出现线性运行时间。n 是输入数据集的大小。

一个很好的例子是使用迭代在数据集中搜索特定值，如下例所示。

function constainsValue(elements, value) {
  for (let element in elements) {
    if (element === value) return true;
  }
  return false
}

我们发现，循环遍历数组中所有元素所需的时间会随着数组大小的增加而增长。但是，如果在到达数组的最后一个元素之前就找到了该元素，会怎样呢？运行时复杂度会发生变化吗？

请记住，大 O 表示法考虑的是最糟糕的情况。在本例中，最坏情况是循环遍历数组中的所有元素。因此，这决定了算法的运行时复杂度。

3. O(n^2) - 二次运行时间

O(n^2) 表示运行时间与输入数据集大小的平方成正比的算法。
例如，使用嵌套迭代或循环来检查数据集是否包含重复项。

function constainsDuplicate(elements) {
  for (let element in elements) {
     for (let item in elements){
       if (element === item) return true;
     }
  }
  return false
}

更深层次的嵌套迭代将产生 O(n^3)、O(n^4) 等运行时复杂度

4. O(log n) - 对数运行时间

在这种情况下，无论输入数据集的大小如何，算法运行所需的时间都会趋于稳定。

一个常见的例子是二分查找之类的搜索算法。二分查找的理念不是处理整个数据，而是每次迭代将工作量减半。达到所需结果所需的运算次数是输入大小的对数（以 2 为底）。

有关此运行时复杂性的更多信息，您可以查看文章末尾的一些资源。

5. O(n log n) - 线性对数运行时间

这里，算法的运行时间取决于运行 n 次对数运算。

大多数排序算法的运行时复杂度为 O(n log n)

6. O(2^n) - 指数运行时间

这发生在算法中，数据集规模每增加一倍，运行时间就会加倍。对于较小的数据集来说，这看起来可能还不错。但随着数据量的增加，执行该算法所需的时间会迅速增加。

一个常见的例子是寻找斐波那契数的递归解决方案。

      function fibonacci(num) {
      if (num <= 1) return 1;

      return fibonacci(num - 2) + fibonacci(num - 1)
   }

7 O(n!) - 阶乘运行时间

在这种情况下，算法的运行时间是阶乘时间。非负整数（n！）的阶乘是所有小于或等于 n 的正整数的乘积。这相当糟糕的运行时间。

对给定数据集执行排列的任何算法都是 O(n！) 的示例。

结论

希望本文能帮助您掌握 Big O 符号的概念。

这里有一些资源，您可以在其中找到有关该主题的更多信息。

有任何补充或疑问？请留言。

谢谢阅读😊。

文章来源：https://dev.to/sarah_chima/the-big-o-notation-an-introduction-34f7