准备编程面试的终极策略
如何更快地准备编码面试
编程面试难度日益加大。几年前,温习关键数据结构并练习 50-75 道编程面试题就足以应对面试了。如今,每个人都能接触到海量的编程问题,而且这些问题也变得越来越难。整个面试过程竞争更加激烈。
在这篇文章中,我想分享我准备编程面试的策略。我的软件工程师生涯大约有 15 年,期间我换了五次工作。我参与过大约 30 个面试环节,总共超过 120 场面试。我也有一些坐在桌子另一边的经验。我参加过 200 多次编程面试和 100 多次系统设计面试。
我认为自己是个相当聪明的工程师,但在白板上解决编程问题时,尤其是在有人评估我的面试环境中,我遇到了一些挑战。为了解决这个问题,我会花相当多的时间进行准备和练习。我之前没有意识到的是,在准备过程中,我遵循了一种系统性的方法。我会做12到15道题,每天练习两个小时。这意味着我可以在一个月内解答350多道题。凭借这种习惯,我成功地通过了FAANG(Facebook、Apple、Amazon、Netflix、Google)的面试。
我是如何做到一边有全职工作一边每天练习12道以上的编程题的呢?嗯,我并不是在解决编程问题,而是在练习如何将问题映射到我已经解决过的问题上。我以前会阅读一个问题,然后花几分钟时间把它映射到我以前见过的类似问题上。如果我能映射它,我就会只关注这个问题与父问题相比有哪些不同的约束条件。如果这是一个新问题,我会尝试解决它,同时也会阅读相关资料,寻找其他人用来设计该算法的巧妙方法。随着时间的推移,我形成了一套问题模式,可以帮助我快速地将一个问题映射到一个已知的问题上。以下是这些模式的一些示例:
- 如果给定的输入已排序(数组、列表或矩阵),那么我们将使用二进制搜索或双指针策略的变体。
- 如果我们要处理元素
k中的顶部/最大/最小/最近的元素n,我们将使用堆。 - 如果我们需要尝试输入的所有组合(或排列),我们可以使用递归回溯或迭代广度优先搜索。
遵循这种基于模式的方法帮助我节省了大量的准备时间。一旦熟悉了某个模式,你就能用它来解决很多问题。此外,这种策略也让我对解决未知问题更有信心,因为我一直在练习将未知问题映射到已知问题上。
在剩下的文章中,我将分享我收集的所有模式,并展示一些示例问题。有关这些问题及相关问题的详细讨论和解决方案,请参阅“深入理解编码面试”。
二分查找示例问题
双调数组最大值
问题描述:
找出给定双调数组中的最大值。如果一个数组先单调递增,然后单调递减,则该数组被认为是双调数组。单调递增或单调递减意味着对于i数组中的任意索引,arr[i] != arr[i+1]。
Example: Input: [1, 3, 8, 12, 4, 2], Output: 12
解决方案
双调数组是已排序数组;唯一的区别是它的第一部分按升序排序,第二部分按降序排序。我们可以使用二分查找的变体来解决这个问题。请记住,在二分查找中我们有start、end和middle索引,并且在每个步骤中我们通过移动起始或结束来减少搜索空间。由于没有两个连续的数字是相同的(因为数组是单调递增或递减的),因此每当我们计算二分查找的索引时,我们都可以比较索引和middle指向的数字来确定我们是在升序部分还是降序部分。所以:middlemiddle+1
- 如果
arr[middle] > arr[middle + 1],我们位于双调数组的第二个(降序)部分。因此,我们需要的数字要么位于中间,要么位于 之前middle。这意味着我们将执行end = middle。 - 如果
arr[middle] <= arr[middle + 1],我们位于双调数组的第一部分(升序)。因此,所需的数字将在 之后middle。这意味着start = middle + 1。
当 时,我们可以中断start == end。由于以上两点, 和 都start将end指向双调数组的最大值。
代码
下面是解决此问题的 Java 代码:
| class MaxInBitonicArray { | |
| public static int findMax(int[] arr) { | |
| int start = 0, end = arr.length - 1; | |
| while (start < end) { | |
| int mid = start + (end - start) / 2; | |
| if (arr[mid] > arr[mid + 1]) { | |
| end = mid; | |
| } else { | |
| start = mid + 1; | |
| } | |
| } | |
| // at the end of the while loop, 'start == end' | |
| return arr[start]; | |
| } | |
| public static void main(String[] args) { | |
| System.out.println(MaxInBitonicArray.findMax(new int[] { 1, 3, 8, 12, 4, 2 })); | |
| System.out.println(MaxInBitonicArray.findMax(new int[] { 3, 8, 3, 1 })); | |
| System.out.println(MaxInBitonicArray.findMax(new int[] { 1, 3, 8, 12 })); | |
| System.out.println(MaxInBitonicArray.findMax(new int[] { 10, 9, 8 })); | |
| } | |
| } |
双指针示例问题
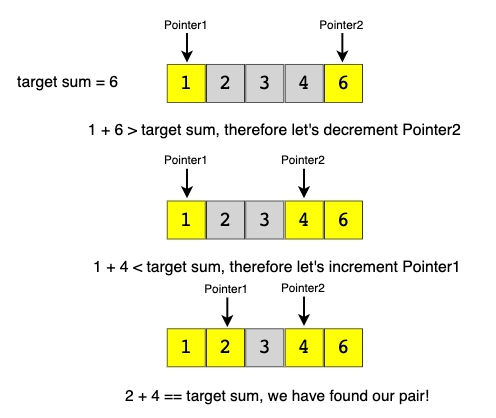
与目标金额配对
问题描述
给定一个排序数字数组和一个目标和,在数组中找到一个和等于给定目标的对。
编写一个函数来返回两个数字(即对)的索引,使得它们加起来等于给定的目标。
Example: Input: [1, 2, 3, 4, 6], target = 6, Output: [1, 3] (The numbers at index 1 and 3 add up to 6: 2+4=6)
解决方案:
由于给定的数组已排序,因此一个强力解决方案是遍历数组,一次取出一个数字,然后通过二分查找法查找第二个数字。该算法的时间复杂度为 O(N*logN)。我们能做得更好吗?
我们可以采用双指针方法。首先,一个指针指向数组的开头,另一个指针指向数组的结尾。每一步,我们都会检查两个指针指向的数字是否相加等于目标和。如果相加,就找到了对应的数字对。否则,我们将执行以下两项操作之一:
- 如果两个指针指向的两个数字之和大于目标和,则我们需要一个和较小的数字对。因此,为了尝试更多数字对,我们可以减少结束指针的值。
- 如果两个指针指向的两个数字之和小于目标和,则意味着我们需要一个和更大的数字对。因此,为了尝试更多数字对,我们可以增加起始指针。
代码
我们的算法如下所示:
示例问题
离原点最近的 K 个点
给定二维平面中的点数组,找到K距离原点最近的点。Example: Input: points = [[1,2],[1,3]], K = 1, Output: [[1,2]]
解决方案
点 P(x,y) 到原点的欧氏距离可以通过以下公式计算: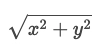
我们可以使用最大堆来找到距离原点最近的 K 个点。首先,我们可以将 K 个点放入堆中。在遍历剩余的点时,如果某个点(比如 P)比最大堆的顶点更靠近原点,我们就将该顶点从堆中移除,并添加 P,以始终将最近的点保留在堆中。
代码
我们的算法如下所示:
示例问题
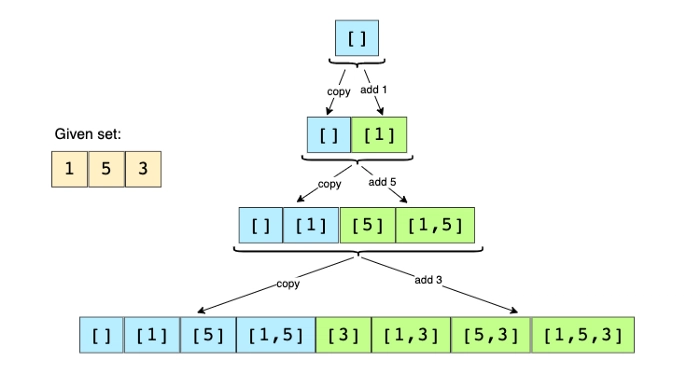
子集
问题描述
给定一个具有不同元素的集合,找到其所有不同的子集。
Example: Input: [1, 5, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3]
解决方案:
要生成给定集合的所有子集,我们可以使用广度优先搜索 (BFS) 方法。我们可以从一个空集开始,逐个遍历所有数字,然后将它们添加到现有集合中以创建新的子集。
让我们以上述示例来介绍算法的每个步骤:
给定集合:[1, 5, 3]
- 从空集开始:[[]]
- 将第一个数字(1)添加到所有现有子集以创建新的子集:[[], [1] ];
- 将第二个数字(5)添加到所有现有子集:[[], [1], [5], [1,5] ];
- 将第三个数字(3)添加到所有现有子集:[[], [1], [5], [1,5], [3], [1,3], [5,3], [1,5,3] ]。
代码
我们的算法如下所示:
示例问题
二叉树路径和
问题描述
给定一棵二叉树和一个数字 S,查找该树是否有一条从根到叶的路径,使得该路径的所有节点值的总和等于 S。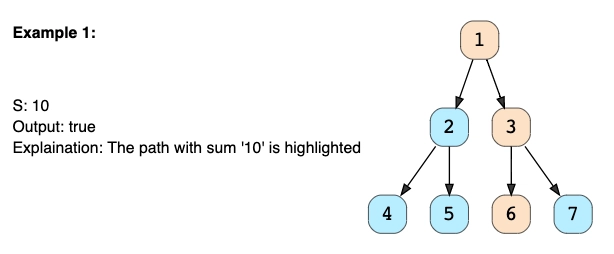
解决方案
当我们尝试搜索从根到叶的路径时,我们可以使用深度优先搜索 (DFS) 技术来解决这个问题。
为了以 DFS 方式递归遍历二叉树,我们可以从根开始,在每一步进行两次递归调用,一次针对左子树,一次针对右子树。
以下是二叉树路径和问题的步骤:
- 从树的根开始 DFS。
- 如果当前节点不是叶节点,则执行两件事:a)从给定数字中减去当前节点的值以获得新的总和 =>
S = S - node.value,b)使用上一步计算出的新数字对当前节点的两个子节点进行两次递归调用。 - 在每一步中,查看当前访问的节点是否为叶节点,以及其值是否等于给定的数字 S。如果两者都为真,则我们找到了所需的从根到叶的路径,因此返回 true。
- 如果当前节点是叶子,但其值不等于给定数字 S,则返回 false。
代码
我们的算法如下所示:
结论
遵循这些模式极大地帮助我节省了准备编程面试的时间。您可以阅读《深入理解编程面试》和《深入理解动态编程面试模式》,了解更多类似的模式及其示例问题。
查看设计大师的一些关于编程面试和系统设计面试的好课程。
文章来源:https://dev.to/arslan_ah/the-ultimate-strategy-to-preparing-for-the-coding-interview-3ace 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com