种

3 种无需 Math.random() 即可生成随机数的神奇方法

2025-05-27

3 种无需 Math.random() 即可生成随机数的神奇方法

你玩过在线旋转赢奖游戏吗？你懂的！就是那种弹出广告说“旋转赢取最新款功能丰富的三星智能手机！”的游戏。我玩过。谁不想免费拥有最新的智能手机呢？可惜的是，无论我玩了多少次都没赢。不过，我还是得到了奖励。奖励源于好奇心，想知道这个欺骗性游戏是如何运作的。我快速谷歌了一下，发现它使用随机数生成器 (RNG) 来运作。它可能是 Math.random()

但是……一台计算机，一个按照人类指令运行的设备，是如何生成随机数的呢？答案是，它不会。它根本就不可能生成随机数。这就是为什么它被称为“伪”随机数生成器（PRNG）。这意味着它是假的，是山寨货。

为什么是仿冒品？

真正的随机数生成器 (RNG) 需要额外的硬件，能够利用现实世界中的随机现象（从掷骰子🎲到测量放射性物质的辐射）作为输入来生成随机数。哇！仅仅利用放射性衰变的随机性来生成数字，就令人难以置信！🤯 慢慢体会一下。

但这些额外的硬件价格不菲，而且除了莱克斯·卢瑟，谁会愿意在口袋里装放射性物质呢？所以大家都同意用PRNG来解决这个问题。

lex_luthor_with_kryptonite

PRNG 并非一种普遍使用的标准算法。当我发现过去 70 年来，由许多聪明人创建的算法不止一种，也不是两种，而是 28 种时，我震惊了。

让我向您展示 3 种Math.random()在 Javascript 中进行替换的神奇方法。

它们是如何工作的？

伪随机数生成器（PRNG）是指使用数学公式产生随机数序列的算法。

https://www.geeksforgeeks.org/pseudo-random-number-generator-prng/

虽然我无法在短时间内研究完所有 28 种算法，但我查阅了 3 种不错的算法。我最初以为它们使用了复杂的数学导数，需要数百行代码。不！我错了。它们只需要 2 到 5 行代码进行基本的算术运算，简单得令人难以置信。这使得初学者更容易理解。

总体而言，这三种算法和 PRNG 都遵循以下通用步骤

  1. 所有这些算法都接受一个称为种子🌱数的输入。这是应用公式的基数。某些算法可以根据要执行的数学运算的需要接受其他输入。

  2. 然后，他们将输入应用于公式，生成的结果就是随机数。

  3. 生成的数字将用作下一次运行的种子。

  4. 重复这些步骤，创建一个数字序列，让我们相信它们是随机的。

有趣的事实

PRNG 与真正的 RNG 的一个独特属性是，PRNG 生成的序列不可避免地会在某个时间点重复出现。

灭霸的重复是不可避免的

1.中二乘法（MSM）

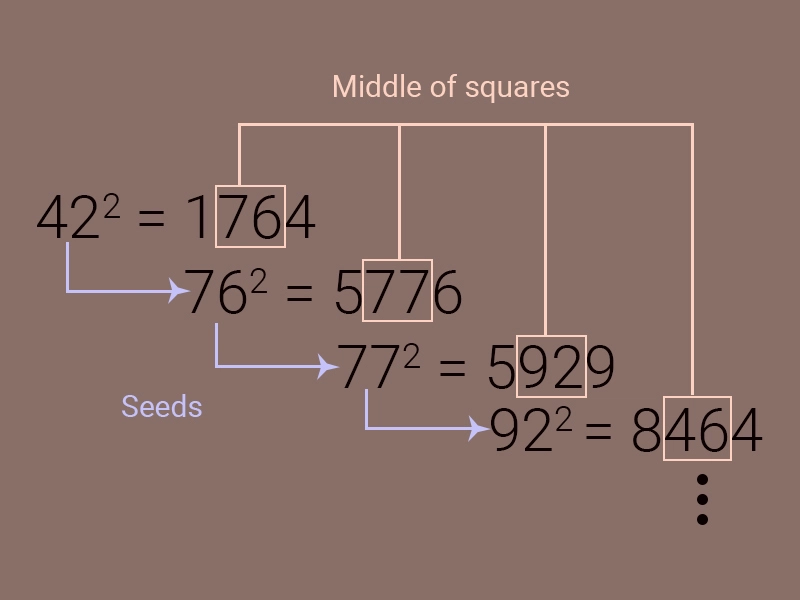
中间平方法 (MSM) 由约翰·冯·诺依曼于 1946 年发明，是第一个用于生成伪随机数序列的方法[1]。实现此方法非常简单。对于一个 n 位随机数序列，

  1. 以一个 n 位数字作为种子。假设它是一个 2 位数字 42。

  2. 计算它的平方。这里，42 的平方是 1764。

  3. 提取平方数的中间 n 位数字，得到序列中的下一个数字。在我们的例子中，下一个数字是 76。

  4. 使用结果作为种子并重复步骤1-4进行下一个循环。

中二法表示法中二法表示法

该算法简单易用，适合初学者练习，帮助他们检验在训练营学习的语言知识。因此，我提供了 JS 实现，希望能帮助他们。

/**

* Middle Square Method implementation in JavaScript

* for a 2-digit random number sequence

**/

var seed;

function middleSquareMethod(){

    var result = (seed * seed).toString().slice(1, 3); // extracting the middle value.

    seed = parseInt(result);

    return parseInt(result);

}
Enter fullscreen mode Exit fullscreen mode

这种方法存在一个问题。有些数字的平方值是奇数，这使得提取中间数字变得困难，例如 15 的情况。15 的平方结果是 225。而我们不能接受 2 作为中间数字，因为我们需要两位数。为了解决这个问题，我们在平方值前面填充零，使其变为偶数。现在 225 变成了 0225，这使得提取中间两位数字 22 变得很容易。解决问题后，代码如下所示。

/**

* Middle Square Method implementation in JavaScript

* for a 2-digit random number sequence

**/  

var seed = 42;

function middleSquareMethod(){

    var result = (seed * seed).toString().padStart(4,"0").slice(1, 3);
    // pad with zero when necessary and extract the middle value.

    seed = parseInt(result);

    return parseInt(result);

}
Enter fullscreen mode Exit fullscreen mode

只需三行代码，我们就能为一个 n 位数字生成最多 8 个n数，之后该序列会重复出现。不过，这其中有一个陷阱。有些种子可能会导致算法的循环周期变短，例如种子 25，这会导致算法无限重复 25。

2. 线性同余生成器（LCG）算法

这个引人入胜的算法比MSM运用了更多数学知识。LCG使用涉及全等运算的线性方程来生成随机数序列。“哇！这些花哨的术语是什么？”我听到你惊呼了。让我来解释一下。

线性是指没有变量的幂大于一的代数方程。

同余是指使用模除运算的方程。

这个算法可能因为术语而显得复杂。但它很容易理解，因为它使用了非常基本的代数和算术运算。它使用了这个特定的方程式X n+1 = (aX n + c) mod m。好了！好了！不用再说数学术语了。我会把它翻译成程序员可以理解的格式。翻译后的方程式是：X = (a * X + c) % m

其中 X 是种子。与 MSM 类似，其结果将用作下一个循环的种子。

a – 是乘数

c – 是增量，

m – 是模量

它有以下条件

  1. m > 0，呃！不可能被零除

  2. 0 < a < m

  3. 0 ≤ c < m 且

  4. 0≤X<m

由于这是一个简单的方程，对计算机来说，求解它轻而易举。对于 MSM 来说，需要将数据从数字转换为字符串，然后再转换为数字，这会对 CPU 造成很大的负担。因此，LCG 是最古老、最著名的随机数生成器算法[2]。因此，LCG在列表中排名第二。

毕竟，增量和种子都可以取值零，但要注意两者都不要取零，否则它只会吐出一串零。

以下是我用 JS 编写的 LCG

/**
* Implementation of the Linear congruential generator
* algorithm in JavaScript
*/
var X,a,c,m;

linearCongruentialGenerator(){

    X = (a * X + c) % m;

    return X;

}
Enter fullscreen mode Exit fullscreen mode

只需两行代码。就两行！写完之后我愣住了😲。一个简单的公式就能实现如此伟大的成就，真是太不可思议了。这更让我对数学产生了敬意。

通过正确的输入组合，我们可以生成一个非常长的序列，甚至比 MSM 开始重复之前还要长。在我的示例中，我使用了数值秘诀[3]中的值 a = 1664525、m = 2^ 32和 c = 1013904223 。

3. Xorshift算法

列表中的第三个算法是 Xorshift 算法。我把这个特殊的算法留到最后。如果说 MSM 对人类来说更容易理解，LCG 对人类和计算机来说都更容易理解，那么 XOR 移位算法则只有计算机才能理解。因为顾名思义，这种方法使用了特殊且很少使用的二进制运算 Xor 和位移位。

请耐心听完。这篇文章用了很多计算机科学术语。我之所以选择这个，是因为我以为自己这辈子都用不到这些二元运算符，就像我以为自己这辈子都看不到小智赢得宝可梦联盟冠军一样。

小智赢得阿罗拉

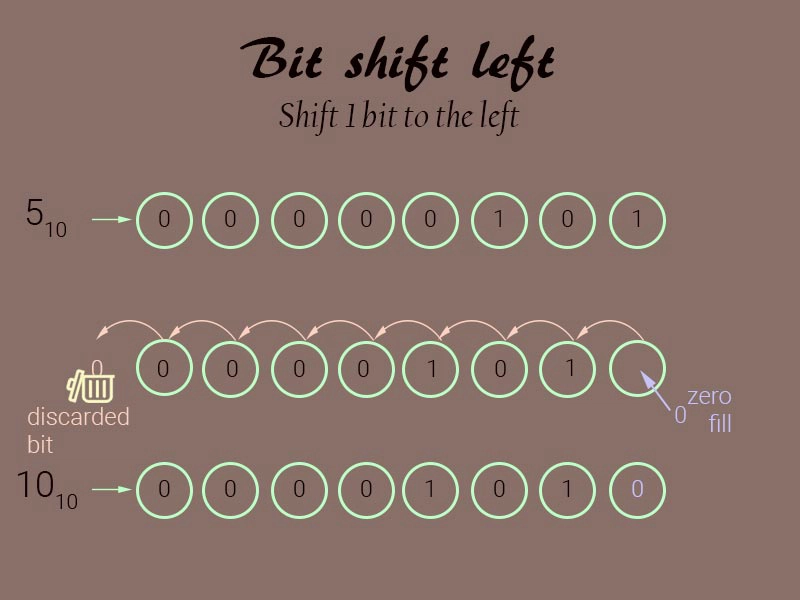
让我来分解一下这个算法。位移位操作的原理是将二进制数中的位向左或向右移动。结果是一个完全不同的数。对于 1 位左移，每个位都向左移动一位。空位用 0 填充，移出的位被丢弃。对于 5 位左移，单位移位操作重复 5 次。以下是一个例子：

42 10在 16 位表示中的二进制等效值为 0000000000101010 2。

向左移 5 位后，它变为 0000010101000000 2 ，这是 1344 10的二进制等效值。

位左移8 位系统中 1 位左移运算的表示

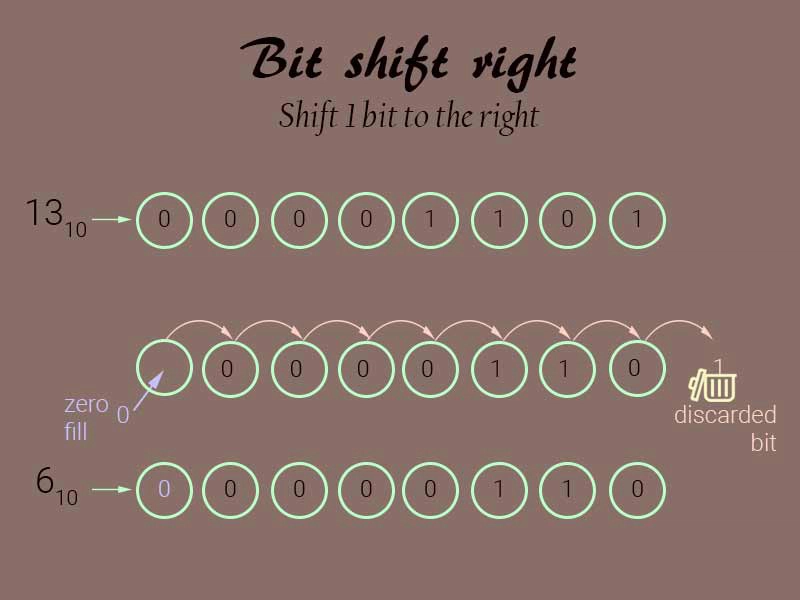
如果我们将 2524 10 - 0000100111011100 2的二进制等值向右移动 5 位，则变为 0000000001001110 2，即十进制的 78 10。右侧其余位将被丢弃。

位右移8 位系统中 1 位右移运算的表示

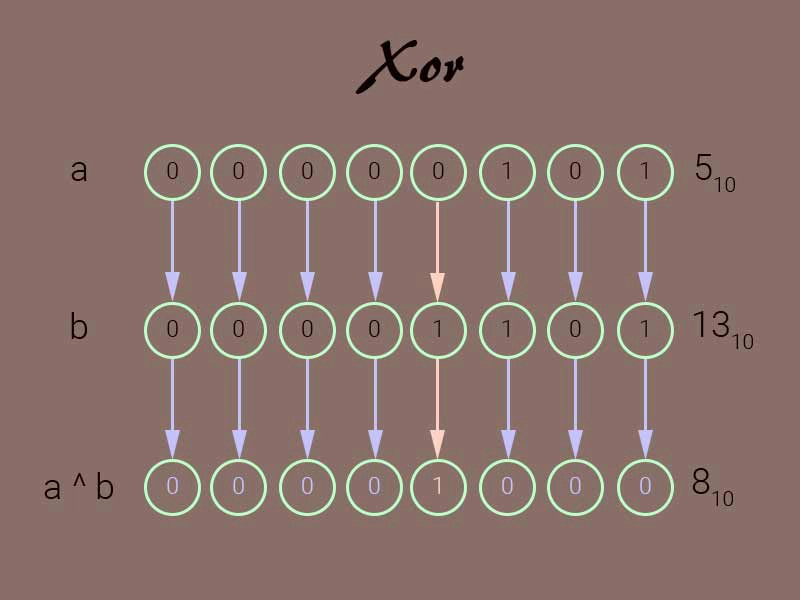
如您所见，位移位运算只需要一个操作数，结果是一个完全不同的数字。而异或运算则需要两个操作数。XOR（Exclusive OR）运算的缩写，用于比较两个二进制数的位，只有当比较的位之一为 1 时，结果的位才为 1。继续前面的例子，42 和 2524 的异或运算如下：

4210 – 0000000000101010 2

252410 – 0000100111011100 2 XOR - 0000100111110110 2相当于 2550 10。

异或运算8位系统中异或运算的表示

异或运算也会产生不同的结果。该算法结合了这两种运算的强大功能。以下是我在 JavaScript 中对异或移位的实现。

/**
* Implementation of XorShift
* algorithm in JavaScript
*/
var seed;

function xorShift(){

  seed ^= seed << 13;

  seed ^= seed >> 17;

  seed ^= seed << 5;

  return seed;
}
Enter fullscreen mode Exit fullscreen mode

该方法对种子执行连续的位移位和异或运算，从而创建一个包含正数和负数的随机序列。算法中的常数 13、17 和 5 来自描述异或移位算法的论文4中建议的三元组列表。该算法直接以二进制（计算机语言）运行，因此比 LCG 更快。

如果您只需要正数，则可以在返回值之前，先取种子的 2 的补码（如果为负数）。如果包含条件，这可能会降低性能。

/**
* Implementation of XorShift
* algorithm in JavaScript
* with 2's complement
*/
function xorShift(){

  seed ^= seed << 13;

  seed ^= seed >> 17;

  seed ^= seed << 5;

  return (seed <0)?~seed+1: seed;
//2's complement of the negative result to make all numbers positive.
}
Enter fullscreen mode Exit fullscreen mode

计算机将正数和负数（称为有符号整数）存储为二进制数，并以 2 的补码形式存储。最左边的位（最高有效位）保留用于表示数字的符号。0 表示正号 (+)，1 表示负号 (-)。

你知道什么是二进制补码吗？别担心，我会解释的。

在二进制补码中，取一个二进制数，例如 11111111 11010011 (-45 10 )，然后将其位翻转。也就是说，将 0 变为 1，反之亦然。最后，将 1 2加到翻转后的数字上。结果 00000000 00101101 2是该数 (45 10 )的正数形式。

-45 10 ➡ 11111111 11010011 2

位反转

00000000 00101100 2

添加 1

00000000 00101100 2 + 1 2

00000000 00101101 2 ➡ 45 10

因此，在我们的算法中，我们总是得到正数。

结论

本文只是PRNG（随机数生成器）这个兔子洞的冰山一角。我想与你分享一些不同的替换方法Math.random()。所有这些示例都会给出整数，这与Math.random()完全相反。Math.random()只会输出0到1之间的随机十进制数。我将转换过程留给你作为练习。你可以使用ES5的特性，例如生成器函数来实现这些。如果有人这样做了，请在评论区留言。

谢谢阅读😊

参考

  • [1] “伪随机数生成器列表”，维基百科。

  • [2][3] “线性同余生成器”，维基百科。

  • [4] “Xorshift RNG” [pdf]，作者：Marsaglia，George，《统计软件杂志》。

封面图片来源：Pixabay上的PIRO4D图像

文章来源：https://dev.to/svijaykoushik/3-amazing-ways-to-generate-random-numbers-without-math-random-4e84
Devto 翻译
PREV
JavaScript：Promise 的概念
NEXT
Theia 1.0 - 终于有了一款优秀的浏览器 IDE 浏览器和桌面的单一来源 不再是父母辈的浏览器 IDE Theia 运行 VS Code 扩展 开放 VSX 谁在使用 Theia？灵活的架构 厂商中立的开源社区 轻松贡献 总结 致谢