每个开发人员必须知道的顶级数据结构和算法

本文由 Aaron Xie 撰写，最初发表于Educative, Inc.

很多人一想到编程面试就心生畏惧。它压力重重，令人精疲力竭，充满挑战。很多时候，光是知道该准备哪些主题就已经让人头疼。不过，今天我们将向你介绍编程面试中会考的主要数据结构和算法。读完这篇文章，你应该会对如何准备才能获得理想的工作有一个清晰的认识。

我们将介绍以下内容：

为什么要学习数据结构和算法？
理解大 O 符号
要学习的重要数据结构
要学习的重要算法
其他主题
如何在下一次编程面试中脱颖而出
资源

为什么要学习数据结构和算法？

编程面试考察你的解决问题能力以及对计算机科学概念的理解。通常情况下，你会有大约 30 到 45 分钟的时间来解决一个复杂问题，但有时也会安排几个简单的技术问题。

这时数据结构和算法就派上用场了。这些面试会考察你链表、队列、排序、搜索等诸多主题，所以做好准备至关重要。公司不仅想测试你的技术知识，还想评估你的解决问题的能力。如果你得到了这份工作，你经常会遇到需要修复的错误，而公司希望确保你能够克服这些障碍。此外，你通常会使用特定的数据结构和算法来优化你的代码，使其尽可能高效地运行。

理解大 O 符号

大 O 符号是一种渐近分析，用于描述算法执行所需的时间。换句话说，它用于描述算法的效率或复杂程度。

大 O描述了算法相对于其输入 $N$ 的执行时间，即随着输入的增加而产生的运行时间。虽然我们可以使用平均情况和最佳情况来分析算法的效率，但我们通常使用大 O 符号表示最坏情况。

今天，你将学习时间复杂度，但请注意，空间复杂度也是一个需要理解的重要概念。运行时复杂度一开始可能比较难理解，所以让我们来看一些例子。

$O(1)$

public int findInt(int[] arr) {
    return arr[0];
}

O(1)描述了一种无论输入如何，始终以常数时间运行的算法。无论数组中包含一千个整数还是一个整数，该函数都将同时执行，因为它只需要一步。

$O(N)$

public int func(int[] arr) {
    for (int i = 1; i <= arr.length; i++) {
        System.out.println(i);
    }
}

$O(N)$ 描述的是一种算法，其运行时间相对于输入 $N$ 线性增加。上述函数将对数组中存储的 $N$ 个值执行 $N$ 步。例如，如果数组长度为 1，则该函数运行 1 个“步”；而如果数组长度为 1000，则该函数运行 1000 个“步”。

在提供的示例中，数组长度是输入大小，迭代次数是运行时间。

$O(N^2)$

public int func(int[] arr) {
    for (int i = 1; i <= arr.length; i++) {
        for (int i = 1; i <= arr.length; i++) {
        System.out.println(i);
        }
    }
}

$O(N^2)$ 描述的是一个函数，其运行时间与输入大小的平方成正比。当存在一个嵌套循环，使得外层循环运行 $N$ 次，而内层循环在外层循环每次迭代时运行 $N$ 次，使得该函数需要 $N^2$ 步时，就会出现这种运行时间。

需要记住的一些规则

忽略常量：使用大 O 符号时，总是会忽略常量。因此，即使运行时复杂度为 O(2N)，我们也称之为 O(N)。
删除次要项：在大 O 时，只需保留最主要的项。例如，$O(N^3 + 50N +1 7)$ 就是 $O(N^3)$。经验法则如下：$O(1)$ < $O(logN)$ < $O(N)$ < $O(NlogN)$ < $O(N^2)$ < $O(2^N)$ < $O(N!)$。

想了解更多关于大 O 符号的知识吗？请查看我们的“什么是大 O 符号”文章。

要学习的重要数据结构

简单来说，数据结构是在计算机中组织和存储数据以便访问和修改数据的方式。你将学习编程面试中会考到的重要数据结构的基础知识。

数组

数组是相同变量类型的元素的集合，这些元素按顺序存储在内存中。它是最流行且最简单的数据结构之一，常用于实现其他数据结构。

数组中的每个项都从 0 开始索引，每个项称为一个元素。另外需要注意的是，在 Java 中，数组的大小无法更改。如果需要动态调整大小，建议使用 List。

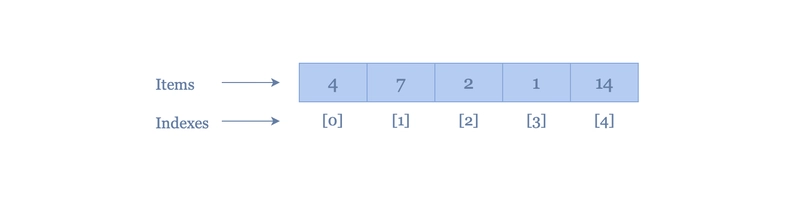
在上面的例子中：

数组的长度为5
索引 3 处的值为 1
在Java中，此数组中的所有值必须是整数类型

在 Java 中初始化数组：

int[] intArray = new int[14];

intArray[3] = 5;
intArray[4] = 3;
intArray[13] = 14;

// Indexes with no value are null

常见面试问题：

查找数组中第一个不重复的整数
按降序重新排列数组
将数组向右旋转一个索引
使用分治法计算子数组的最大和

链接列表

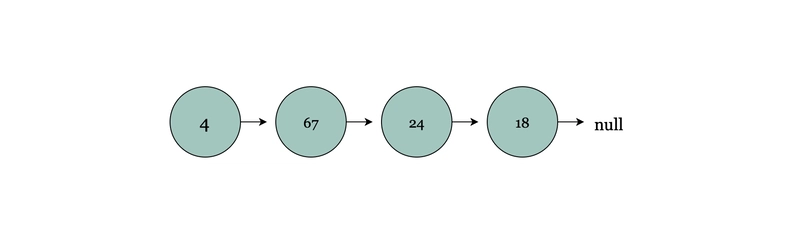
链表是由相互链接的节点组成的线性序列。每个节点包含一个值和一个指向列表中下一个节点的指针。与数组不同，链表没有索引，因此必须从第一个节点开始遍历每个节点，直到到达第 n 个节点。最后，最后一个节点将指向空值。

第一个节点称为头，最后一个节点称为尾。下图展示了一个单链表。

链表有许多有用的应用：

实现堆栈、队列和哈希表
创建目录
多项式表示和算术运算
动态内存分配

Java中链表的基本实现：


import java.io.*; 

// Java program to implement 
// a Singly Linked List 
public class LinkedList { 

    Node head; // head of list 

    // Linked list Node. 
    // This inner class is made static 
    // so that main() can access it 
    static class Node { 

        int data; 
        Node next; 

        // Constructor 
        Node(int d) 
        { 
            data = d; 
            next = null; 
        } 
    } 

    // Method to insert a new node 
    public static LinkedList insert(LinkedList list, int data) 
    { 
        // Create a new node with given data 
        Node new_node = new Node(data); 
        new_node.next = null; 

        // If the Linked List is empty, 
        // then make the new node as head 
        if (list.head == null) { 
            list.head = new_node; 
        } 
        else { 
            // Else traverse till the last node 
            // and insert the new_node there 
            Node last = list.head; 
            while (last.next != null) { 
                last = last.next; 
            } 

            // Insert the new_node at last node 
            last.next = new_node; 
        } 

        // Return the list by head 
        return list; 
    } 

    // Method to print the LinkedList. 
    public static void printList(LinkedList list) 
    { 
        Node currNode = list.head; 

        System.out.print("LinkedList: "); 

        // Traverse through the LinkedList 
        while (currNode != null) { 
            // Print the data at current node 
            System.out.print(currNode.data + " "); 

            // Go to next node 
            currNode = currNode.next; 
        } 
    } 

    // Driver code 
    public static void main(String[] args) 
    { 
        /* Start with the empty list. */
        LinkedList list = new LinkedList(); 

        // 
        // ******INSERTION****** 
        // 

        // Insert the values 
        list = insert(list, 1); 
        list = insert(list, 2); 
        list = insert(list, 3); 
        list = insert(list, 4); 
        list = insert(list, 5); 
        list = insert(list, 6); 
        list = insert(list, 7); 
        list = insert(list, 8); 

        // Print the LinkedList 
        printList(list); 
    } 
}

常见面试问题：

反转链接列表
查找链表中的中间值
删除链接列表中的循环

堆栈

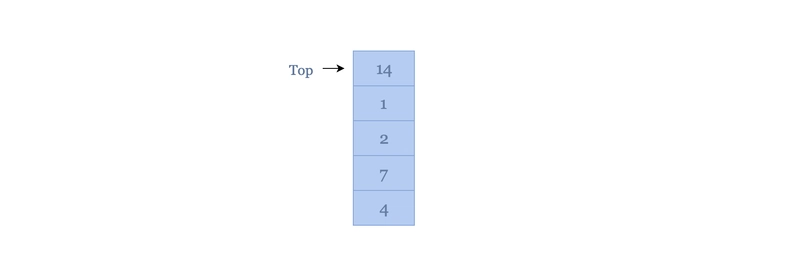
栈是遵循 LIFO（后进先出）顺序的线性数据结构。那么，这是什么意思呢？想象一下一叠盘子。最后一个放在栈顶的盘子是最先取出的。栈就是这样工作的：最后一个添加的值是最先移除的。

把栈想象成一个可以添加和移除元素的集合。栈中最常见的函数是 push、pop、isEmpty 和 peek。

堆栈有许多有用的应用：

回溯到之前的状态
表达式求值和转换

常见面试问题：

使用堆栈检查括号是否平衡
在一个数组中实现两个堆栈
使用堆栈获取下一个更大的元素

队列

队列与栈非常相似，因为它们都是具有动态大小的线性数据结构。然而，队列是 FIFO（先进先出）数据结构。为了形象地理解这种数据结构，想象一下你正在排队等待坐过山车。最先排队的人可以离开队伍去乘坐过山车。

在这个数据结构中，元素从“后面”进入，从“前面”离开。队列中的标准函数是入队、出队、后队、前队和 isFull。

队列有许多有用的应用：

当一个资源被多个消费者共享时
创建目录
当数据在两个资源之间异步传输时

常见面试问题：

反转队列的前 k 个元素
使用队列生成从 1 到 n 的二进制数

图表

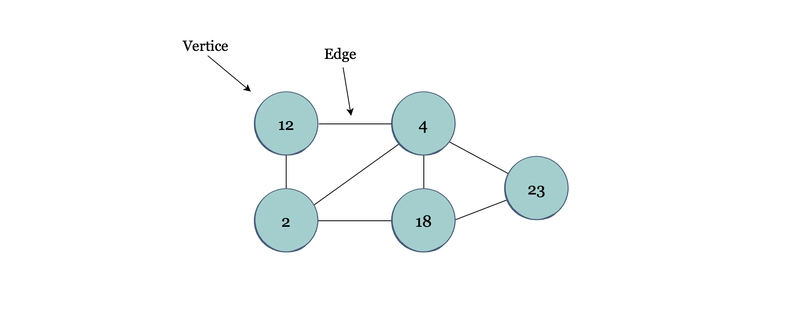
图是通过边连接的顶点（节点）的集合，从而形成网络。

在上面的例子中，顶点集为（12、2、4、18、23），边为（12-2、12-4、2-4、4-18、4-23、18-23、2-18）。

图是一种用途广泛的数据结构，可以解决许多实际问题。图常用于 LinkedIn 或 Facebook 等社交网络。随着 GraphQL 的兴起，数据正以图或网络的形式进行组织。

图的基本实现：

import java.util.*; 

class Graph { 

    // A utility function to add an edge in an 
    // undirected graph 
    static void addEdge(ArrayList<ArrayList<Integer> > adj, 
                        int u, int v) 
    { 
        adj.get(u).add(v); 
        adj.get(v).add(u); 
    } 

    // A utility function to print the adjacency list 
    // representation of graph 
    static void printGraph(ArrayList<ArrayList<Integer> > adj) 
    { 
        for (int i = 0; i < adj.size(); i++) { 
            System.out.println("\nAdjacency list of vertex" + i); 
            for (int j = 0; j < adj.get(i).size(); j++) { 
                System.out.print(" -> "+adj.get(i).get(j)); 
            } 
            System.out.println(); 
        } 
    } 

    // Driver Code 
    public static void main(String[] args) 
    { 
        // Creating a graph with 5 vertices 
        int V = 5; 
        ArrayList<ArrayList<Integer> > adj  
                    = new ArrayList<ArrayList<Integer> >(V); 

        for (int i = 0; i < V; i++) 
            adj.add(new ArrayList<Integer>()); 

        // Adding edges one by one 
        addEdge(adj, 0, 1); 
        addEdge(adj, 0, 4); 
        addEdge(adj, 1, 2); 
        addEdge(adj, 1, 3); 
        addEdge(adj, 1, 4); 
        addEdge(adj, 2, 3); 
        addEdge(adj, 3, 4); 

        printGraph(adj); 
    } 
}

常见面试问题：

找到两个顶点之间的最短路径
检查两个顶点之间是否存在路径
在图中寻找“母顶点”

哈希表

什么是哈希？
在深入研究哈希表之前，我们有必要先了解一下什么是哈希。

哈希算法是将对象分配到唯一索引（称为键）的过程。每个对象都使用键值对进行标识，对象的集合称为字典。

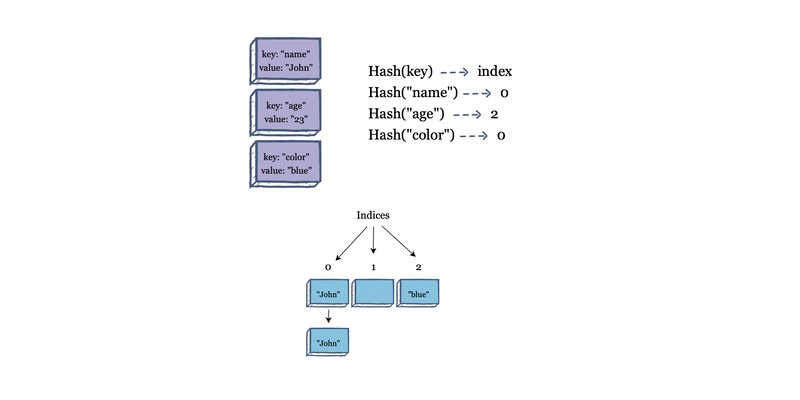
哈希表的实现方式是将元素存储在数组中，并通过键来标识它们。哈希函数接收一个键，并返回存储该值的索引。

因此，无论何时将键输入哈希函数，它总是会返回相同的索引，该索引将标识关联的元素。此外，如果哈希函数收到一个返回已使用索引的唯一键，则可以创建一个带有链表的元素链。

哈希表有许多有用的应用：

当一个资源被多个消费者共享时
密码验证
链接文件名和路径

常见面试问题：

查找数组中的对称对
使用散列对列表进行并集和交集

二叉搜索树

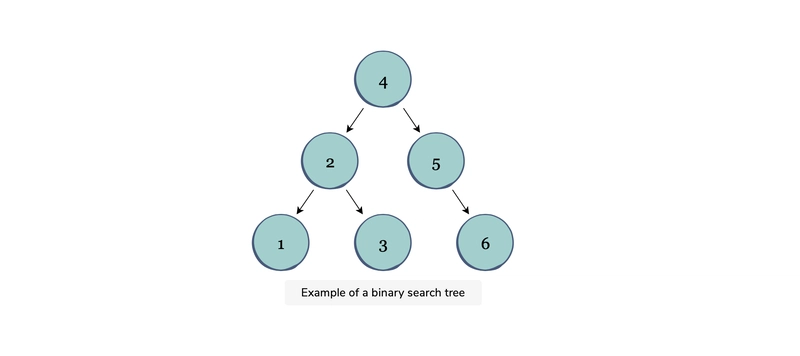
二叉搜索树是由节点组成的二叉树数据结构。节点的排列具有以下属性：

左子节点始终包含小于父节点的值。
右子节点始终包含大于父节点的值。
两个子节点也将是二叉搜索树。

二叉搜索树在许多搜索应用中都有使用，也用于确定 3D 游戏中需要渲染的对象。由于分层数据非常常见，这种数据结构在工程项目中被广泛使用。

常见操作：

搜索 - 搜索元素
插入——在树中插入一个元素
前序遍历——以前序方式遍历树
中序遍历——按顺序遍历树
后序遍历——以后序方式遍历树

常见面试问题：

在二叉搜索树中查找第 k 个最大值
在二叉搜索树中查找最小值
使用广度优先搜索遍历给定目录

继续学习。

无需费力翻看视频或钻研数百道题目，即可轻松掌握面试常见问题。Educative 的文本课程易于浏览，并配备实时编程环境，让学习更加快速高效。

深入理解编码面试：编码问题模式

要学习的重要算法

递归

递归是一种函数直接或间接调用自身的实践。被调用的相应函数称为递归函数。虽然递归通常与算法相关，但将其理解为解决问题的一种方法或方法论可能更有帮助。

那么递归为什么有用呢？或者说它到底是什么？让我们以计算阶乘为例，看看如何使用递归。

public static long factorial(int number){        
        //base case - factorial of 0 or 1 is 1
        if(number <=1){
            return 1;
        }        
        return number*factorial(number - 1);
    }

在上面的例子中，函数从数字 n 开始。当函数被调用时，它将调用 factorial(n - 1)。假设 n 的值为 4，函数将返回

$4 * 阶乘(3) -> 4 * 3 * 阶乘(2) -> 4 * 3 * 2 * 阶乘(1)$

一旦 $n = 1$，函数将返回 $factorial(1) = 1$，我们得到 $factorial(4)$ 等于 $4 * 3 * 2 * 1$，即 24。

在这里，你可以看到递归的威力。递归是一种广泛使用的方法，它将一个复杂的问题分解成更小的子问题，直到我们能够解决它。使用递归，你可以简化许多原本难以解决的复杂问题。

需要更多解释？阅读我们的“什么是递归？”。 Edpresso 截图在这里。

冒泡排序

冒泡排序是一种简单的排序算法，如果相邻元素的顺序不正确，则交换它们。该算法将多次迭代数组，直到元素的顺序正确为止。

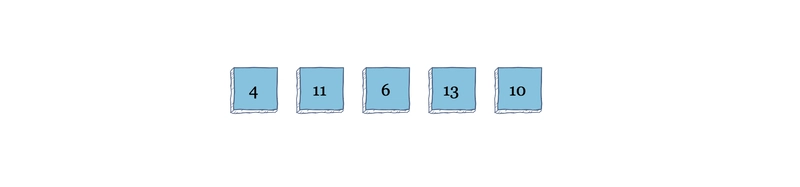
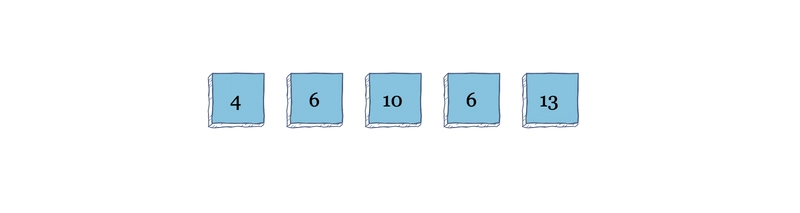
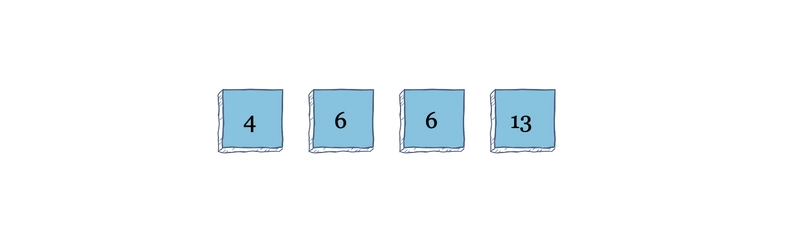
假设我们有一个如下所示的数组。

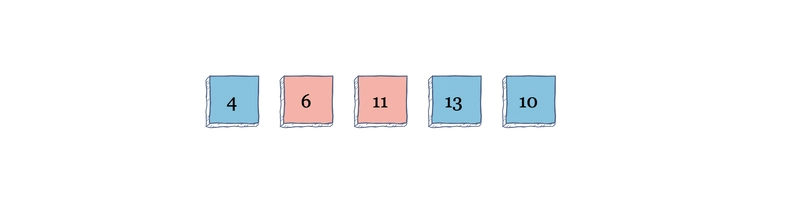
当算法从索引 0 开始从左到右扫描数组进行第一次迭代时，它会比较索引 $i$ 与索引 $i + 1$。在索引 1 处，它会发现 11 大于 6，并将两者交换。

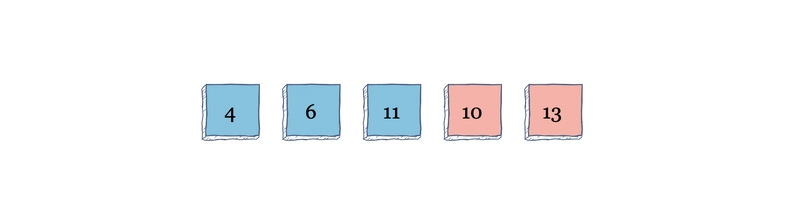
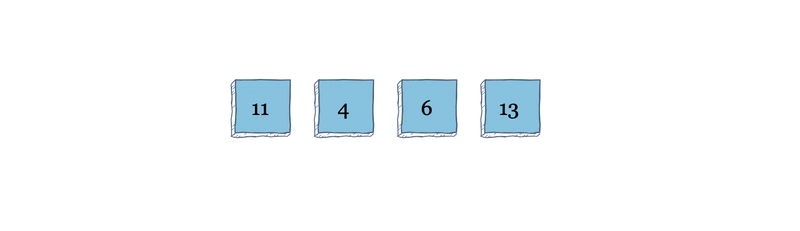
随着算法继续进行第一次迭代扫描，它将发现 13 大于 10，并将两者交换。

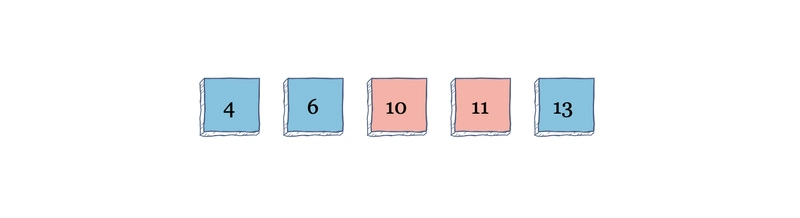
接下来，它将对数组进行第二次迭代。当它发现 11 大于 10 时，它将交换索引 2 和 3 中的值。

算法将对数组进行第三次迭代扫描，并且由于第三次迭代不需要再进行任何交换，因此算法将结束。

可以看出，冒泡排序在处理大量元素时性能不佳，因此它主要用作教学工具。它的运行时复杂度为 O(n^2)。

实现冒泡排序：

public static void bubble_srt(int array[]) {
        int n = array.length;
        int k;
        for (int m = n; m >= 0; m--) {
            for (int i = 0; i < n - 1; i++) {
                k = i + 1;
                if (array[i] > array[k]) {
                    swapNumbers(i, k, array);
                }
            }
            printNumbers(array);
        }
    }

选择排序

选择排序是一种将元素集合分为已排序和未排序的算法。在每次迭代中，该算法在未排序组中找到最小的元素，并将其移动到已排序组的末尾。

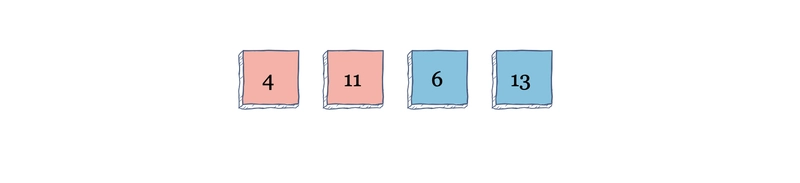
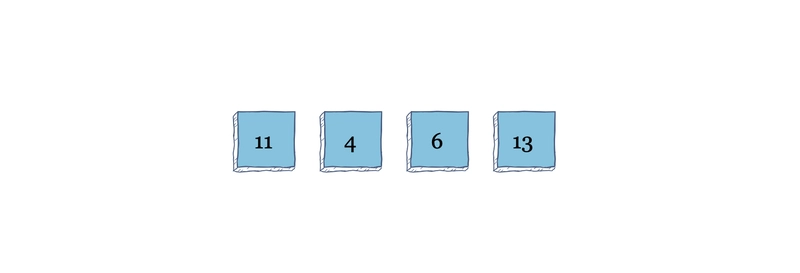
让我们看一个例子：

首先，所有元素都是未排序的。在第一次迭代中，算法将遍历每个元素，并将 4 确定为最小值。算法会将未排序组中的第一个元素 11 与未排序组中的最小元素 4 进行交换。

现在，排序组是索引 0，未排序组是索引 1 到索引 3。对于第二次迭代，算法将从索引 1 开始扫描数组，并将 6 标识为未排序组中的最小值。它将交换 11 和 6。

现在，已排序组位于索引 0 到索引 1 之间，未排序组位于索引 2 到索引 3 之间。第三次迭代时，算法将从索引 2 开始，找到 11 作为最小值。由于 11 已经在正确的索引中，因此不会移动。至此，算法结束。

与冒泡排序类似，选择排序通常是一种较慢的算法。它的运行时复杂度也为 O(n^2)。

实现选择排序：

public static int[] doSelectionSort(int[] arr){

        for (int i = 0; i < arr.length - 1; i++)
        {
            int index = i;
            for (int j = i + 1; j < arr.length; j++)
                if (arr[j] < arr[index]) 
                    index = j;

            int smallerNumber = arr[index];  
            arr[index] = arr[i];
            arr[i] = smallerNumber;
        }
        return arr;
    }
}

插入排序

插入排序是一种简单的排序算法，它通过一次对一个元素进行排序来构建最终的数组。它是如何工作的？

检查每个元素并将其与左侧的排序元素进行比较
按照排序元素的正确顺序插入项目

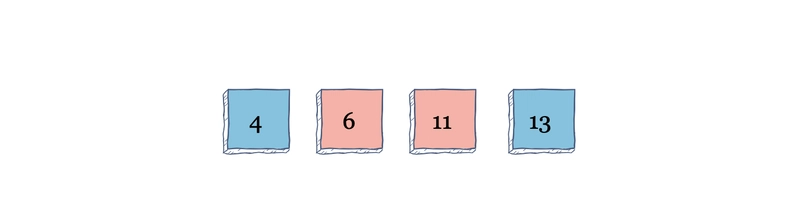
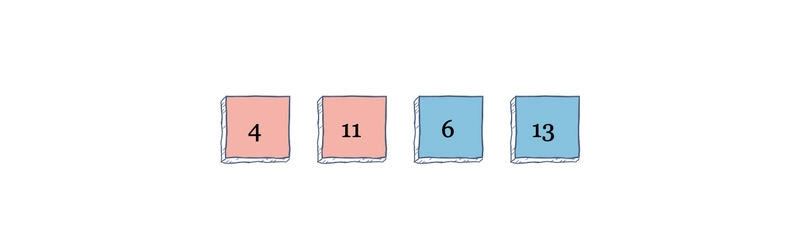
我们来看一个例子。

算法从索引 0 开始，值为 11。由于 11 左侧没有元素，所以它保持原样。现在，转到索引 1。它左侧的值为 11，这意味着我们交换 11 和 4。

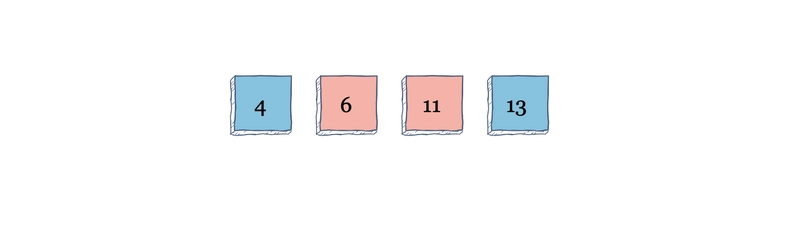
再次，算法查找 4 的左侧。由于 4 左侧没有元素，所以它停留在原处。接下来，查找索引 2。值为 6 的元素向左查找。由于它小于 11，所以两者互换。

元素 6 再次向左查找，但由于 4 小于 6，它停留在原处。接下来，我们转到索引 4 处的元素。算法再次向左查找，但由于 11 小于 13，它停留在原处。现在，算法完成了。

插入排序几乎总是比冒泡排序和选择排序更高效，因此在处理少量元素时更常用。与其他两种排序算法类似，插入排序的运行时间也是 O(n^2) 的平方级数。

实现插入排序：

public static int[] doInsertionSort(int[] input){

        int temp;
        for (int i = 1; i < input.length; i++) {
            for(int j = i ; j > 0 ; j--){
                if(input[j] < input[j-1]){
                    temp = input[j];
                    input[j] = input[j-1];
                    input[j-1] = temp;
                }
            }
        }
        return input;
    }

二分查找

二分查找是查找元素最有效的算法。该算法通过比较数组或列表的中间元素与目标元素来工作。如果值相同，则返回元素的索引。如果不相同，则将列表减半。

如果目标值小于中间值，则新列表为左半部分。如果目标值大于中间值，则新列表为右半部分。

这个过程持续进行，你不断分割列表并搜索其中一半，直到搜索算法找到目标值并返回其位置。该算法的运行时复杂度为 O(log2n)。需要注意的是，二分查找仅在列表已排序的情况下有效。

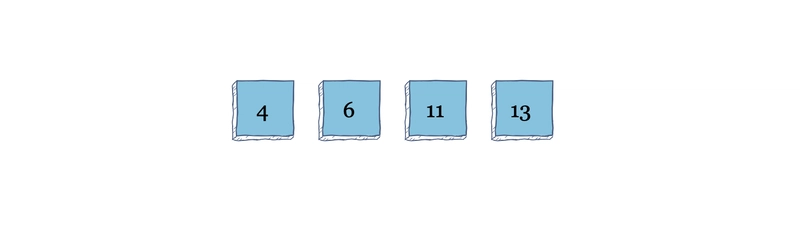
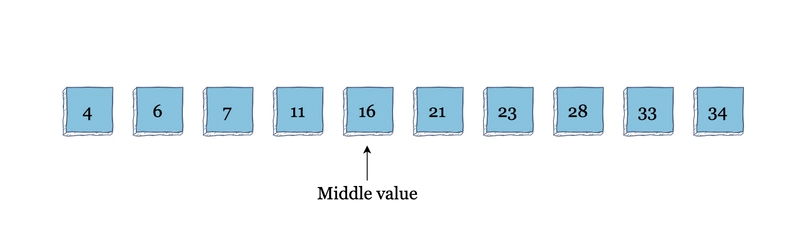
为了形象化二分查找，假设您有一个包含十个元素的排序数组，并且您正在寻找索引 33。

这个数组的中间值是16，算法把它和33进行比较，33大于16，所以算法就把数组分割开，在后半部分查找。

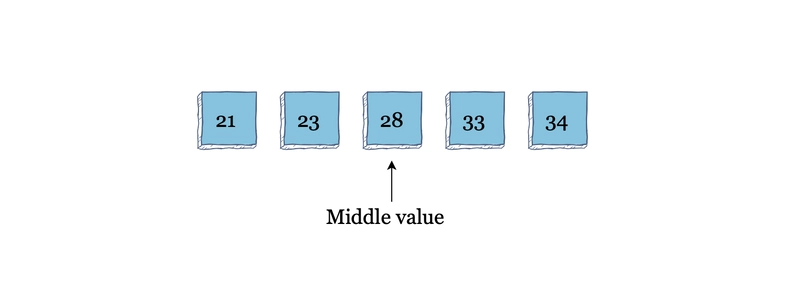
新的中间值为 28。由于 33 大于 28，因此算法在数组的后半部分进行搜索。

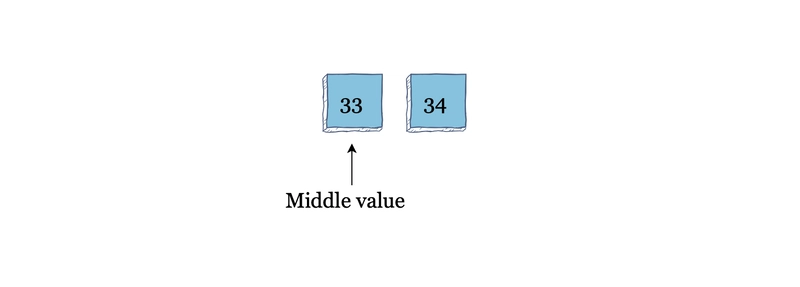
将数组再次拆分为右半部分后，新的中间值为 33。算法发现中间值与目标值相同，因此返回元素的位置。

实现二分查找：

int binarySearch(int arr[], int l, int r, int x) 
    { 
        if (r >= l) { 
            int mid = l + (r - l) / 2; 

            // If the element is present at the 
            // middle itself 
            if (arr[mid] == x) 
                return mid; 

            // If element is smaller than mid, then 
            // it can only be present in left subarray 
            if (arr[mid] > x) 
                return binarySearch(arr, l, mid - 1, x); 

            // Else the element can only be present 
            // in right subarray 
            return binarySearch(arr, mid + 1, r, x); 
        } 

        // We reach here when element is not present 
        // in array 
        return -1; 
    }

其他主题

请记住，我们今天介绍的概念只是入门介绍。深入理解这些概念并练习编程题非常重要。以下是我们建议您熟悉的其他主题：

如何在下一次编程面试中脱颖而出

提前计划：在做任何事情之前，你首先应该做的就是制定一个全面的学习计划。确定你认为需要更多练习的主题，并制定一个可以坚持的学习计划。你应该做好持续学习的准备。一般来说，四到六周是准备面试的最佳时间。
编程语言：选择一种你觉得用起来顺手的编程语言。你能用这种语言在 25 分钟左右轻松编写出解决方案吗？开发人员会使用的一些流行语言包括 Java、Python、JavaScript 或 C++。
公司：在参加任何面试之前，你都应该了解这家公司。了解公司的文化和价值观至关重要，这样才能确保你与公司保持一致，并在面试的非技术方面做好更充分的准备。你还应该研究公司测试的常见问题。通过这样做，你可以进行有针对性的练习，为面试做好准备。
行为面试：即使你觉得自己已经准备好应对技术面试，也别忘了行为面试。公司希望通过行为面试来确认你是否适合该职位和公司。查看我们的行为面试指南，为面试做好充分准备。

现在，你应该对面试前需要做的事情有了大致的了解。你还有很多东西要学，不过不用担心。如果你想继续学习，可以查看“编码面试”提供的资源，或者查看我们“编程语言面试”系列下的“Python”、“Java”或“JavaScript” 面试准备课程。

资源

这是有关编码面试和一般计算机科学主题的资源列表。

文章

精通 JavaScript 面试：学习如何回答最热门的 JavaScript 面试问题
行为面试：面试中回答行为问题的指南
Java 面试准备：学习 15 个常见的 Java 面试问题，以便为下一次面试做好更充分的准备

文章来源：https://dev.to/educative/top-data-structs-and-algorithms-every-developer-must-know-241a