Big(O) 符号总结！

Big(O) 是我们以标准方式比较两个程序的算法复杂度的方法

Big(O) 是一种算法复杂度度量，它定义了输入数量与算法处理这些输入所采取的步骤之间的关系。

总的来说big(O)，程序在输入规模变化时必须完成的工作量。Big(O)在其他方面，可以用来定义时间和空间复杂度

Big(O)从最佳情况到最坏情况的表格。

如何使用 BIG(O) 计算时间复杂度

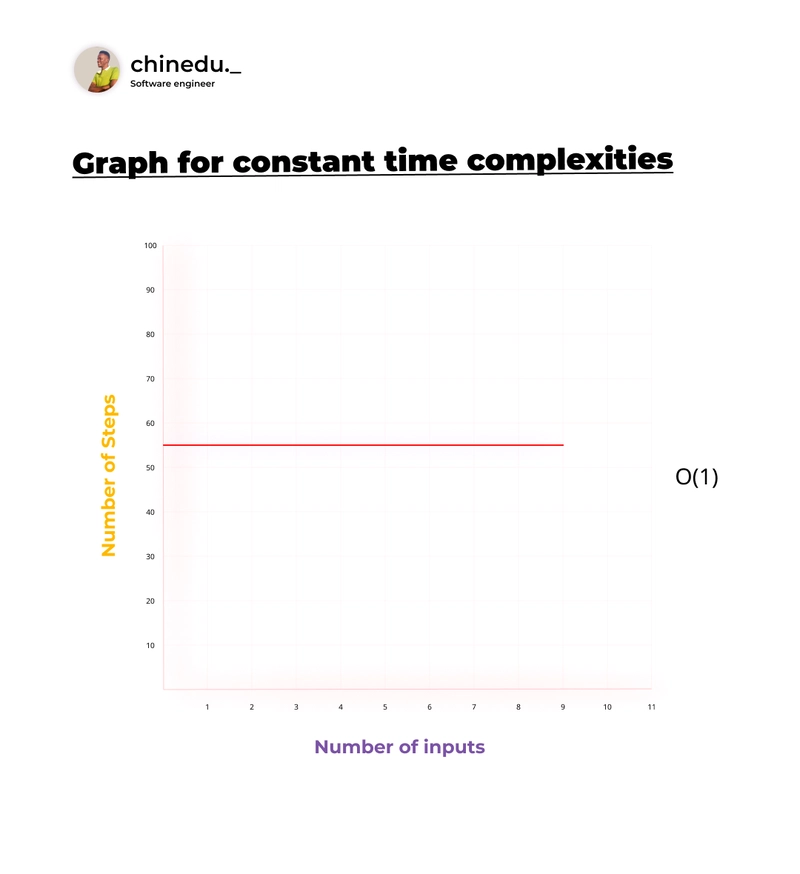
常数复杂度 O(1)

在恒定的复杂性中，无论输入的大小如何，完成程序执行所采取的步骤总是相同的。

执行将获取数组中某个位置的元素（例如获取D数组中索引为 3 的字母表）。

上述操作只需一步即可完成。上面的示例中，该getAlphabetAt方法获取数组中位于常量位置的特定元素。

无论数组中有多少个字母，该getAlphabetAt方法始终执行两个步骤。

1. 首先获取某个位置的元素。

2. 第二，console.logs()将结果输出到控制台。

因此，我们可以说，复杂性是恒定的，因为它不会随着输入而变化。

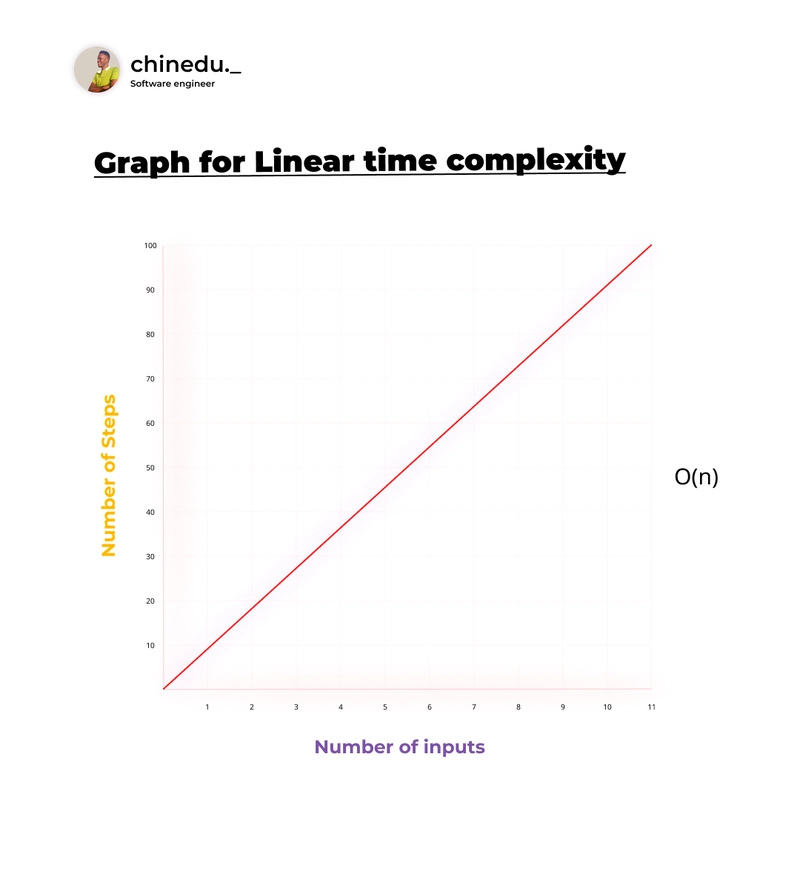
线性复杂度 O(N)

在具有线性复杂度的算法中，输入的单个单位增加会导致完成程序执行所需的步骤的单位增加。

一个例子是计算数组中每个元素的幂。

这将是线性的，因为随着数组的增长，它将对该元素执行更多的单位操作。

上述方法getCubicValues()需要3个步骤才能完成。

params因此，对于作为to方法传递的数组中的每个项目getCubicValues()，该方法都会找到数组中每个项目的立方体，然后将其记录到console。

具有线性复杂度的函数用位置方向增加的直线图表示。

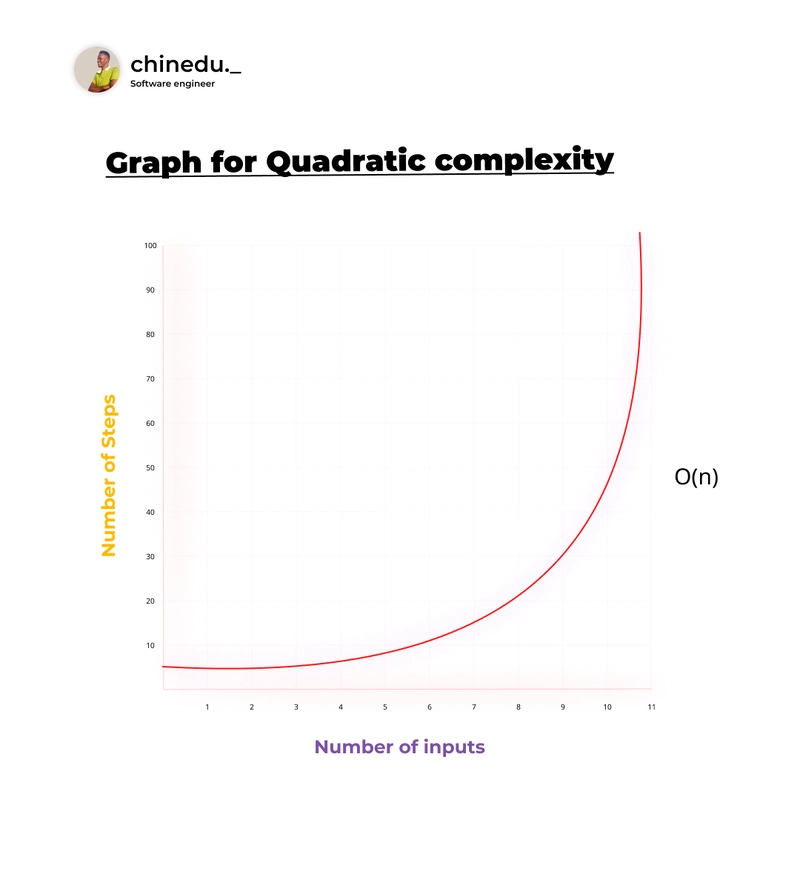
二次复杂度

在具有二次复杂度的算法中，输出步骤随着输入的增加而二次增加。

在上面的图形示例中，该getProductValue方法将该数组中的每个元素与其他元素相乘。

有两个循环，其中外循环对每个项目进行评级，并且对外循环中的每个项目进行评级，而内循环也对每个项目进行迭代。

这使得步骤数为N*N数组N中元素的数量

空间复杂度的 BIG(O) 符号

为了获得空间复杂度，我们计算算法输入元素所需的空间量。

复杂性中的最佳情况与最坏情况

有两种类型的复杂性

1. 最佳情况

2. 最坏的情况

最佳情况

这是理想情况下算法的复杂性。

举个例子，假设我们想在包含 N 个项目的数组中搜索项目 A。

在最佳情况下，我们会在第一个索引处找到该项目，我们可以说其复杂性为O(1)。

最坏的情况

在最坏的情况下，假设我们在nth index（最后）找到该项目，在这种情况下，我们可以说复杂度将是数组中项目总数O(N)。N

总而言之，算法复杂度是用来衡量算法在所花费的时间和空间方面的性能的工具。

谢谢你一直陪着我。你太棒了。

如果您喜欢，请在Twitter和Instagram上关注我，如果有任何改进或代码错误，请在下面的评论部分告诉我或发送 dm。

再次感谢，暂时告别。爱你❤❤❤。