完成了 JavaScript 数据结构课程，以下是我学到的关于图形（+ Dijkstra 算法）的知识。

首先，什么是Graph？

我们如何使用 JavaScript 实现图表？

基本实现

寻找最短路径（Dijkstra算法）

结论

资源

在本系列文章中，我们概述了链表、堆栈、队列、二叉搜索树、二叉堆和哈希表等数据结构。我们还以哪种数据结构适合存储词汇数据为例进行了分析，最终发现哈希表目前是最合适的选择。

（这是我学习所有这些算法和数据结构的课程：Colt Steele 的 JavaScript 算法和数据结构大师班 - Udemy）

该数据用于我的 Chrome 扩展项目，目前其结构如下：

// Result of console.log(MainData)
arbitrary: { category: "Book1", definition: "based on random choice or personal whim, rather than any reason or system.", tag: ["adj"]};
interpretation: { category: "Machine Learning", definition: "the action of explaining the meaning of something", tag:["noun"]};
intuitive: { category: "Book2", definition: "using or based on what one feels to be true even without conscious reasoning; instinctive", tag: ["adj"]};
precision: { category: "Machine Learning", definition: "the quality, condition, or fact of being exact and acurate", tag: ["noun"]};

每个词汇表都是一个唯一的字符串，因此我们使用单词作为索引。在此结构下，删除/编辑/插入的时间复杂度为 O(1)。

但是，如果我们用图来代替哈希表来处理数据会怎么样呢？它的成本还会像现在一样低吗？或者它还能提升性能吗？在本文中，我们将进行研究。

首先，什么是Graph？

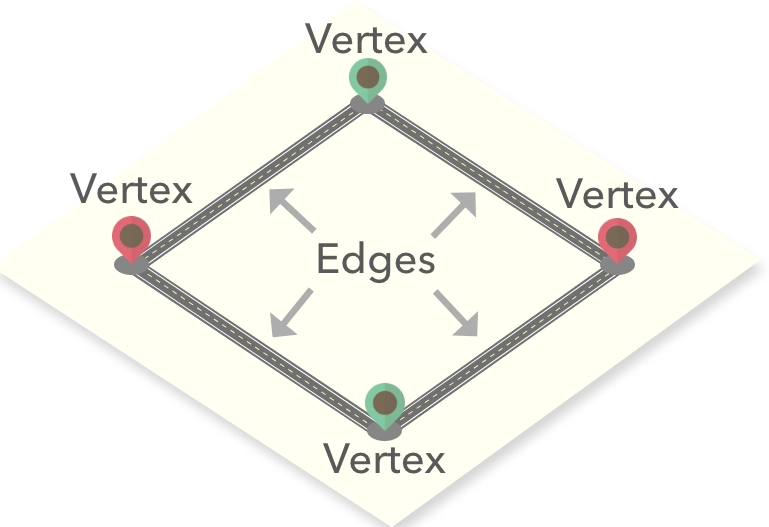
图是一种非常常见且应用广泛的数据结构。所有图都包含两种类型的元素——顶点和边，这使得我们的图独一无二。

正如我们在上图中所看到的，顶点与节点相同，它是一个存储数据的盒子。边是连接顶点的连接。

两种类型的图表

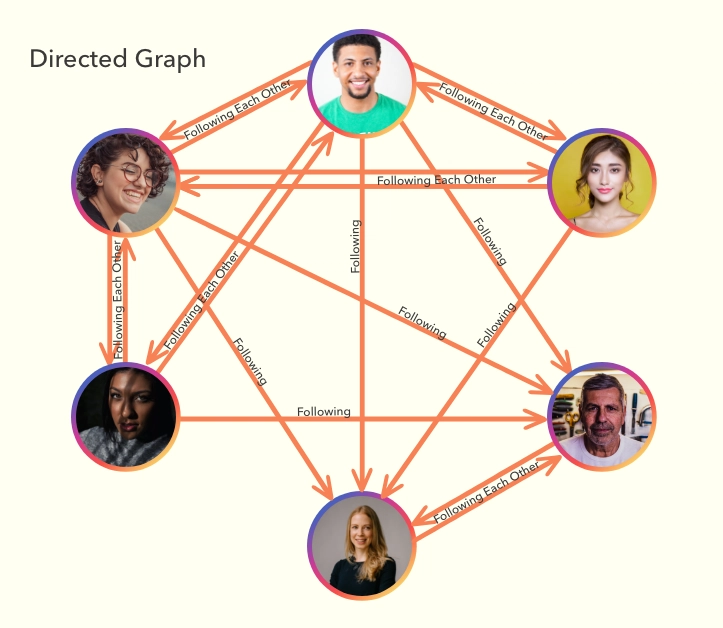
图有两种类型——有向图和无向图。
例如，我们可以将 Instagram 或 Twitter 的关系解释为有向图，因为关系之间存在方向。当你关注某人时，你就建立了连接，能够在你的时间线上看到他们的内容，但只要他们不关注你，他们就看不到你的内容——这就创建了一条指向你的有向边。

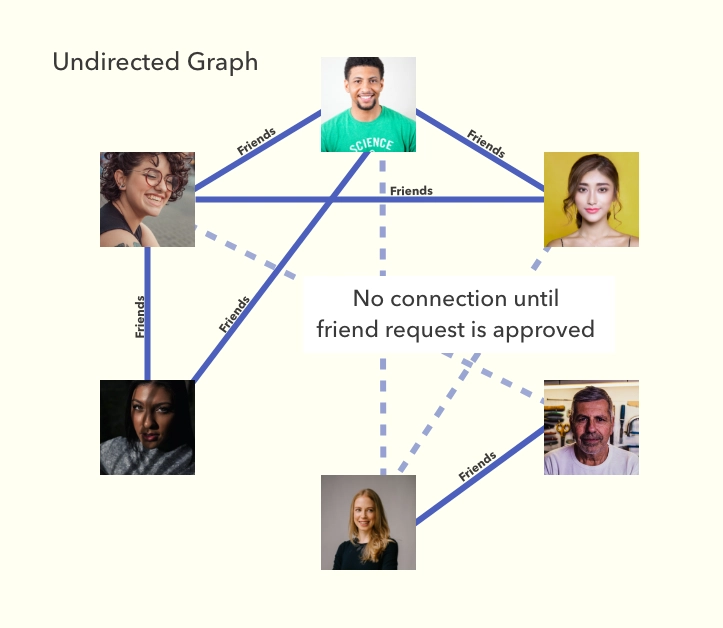
与有向图不同，无向图适用于不需要表示方向的情况，例如 Facebook 关系。当你创建一条边（接受好友请求）时，你和好友都能自动看到彼此的内容。因此无需表示方向。

加权/非加权图

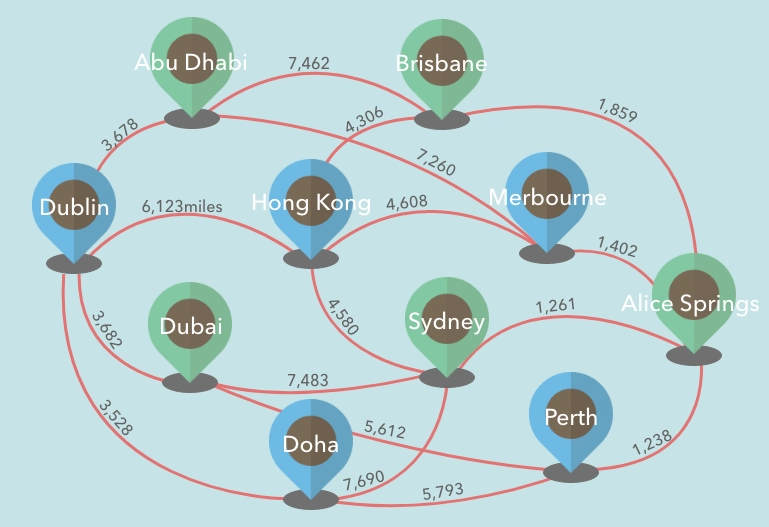
图的另一个用处是，我们可以为每条边赋值作为权重/距离。我们称这些图为加权图。

例如，如果我们决定绘制航班连接，我们可以使用加权图。我们可以为连接机场的边分配一个数字，这样我们就可以表示它们之间的距离。

我们如何使用 JavaScript 实现图表？

实现它有几种不同的方法，例如邻接矩阵、关联矩阵等。今天我们将研究最常见的方法之一——邻接表。

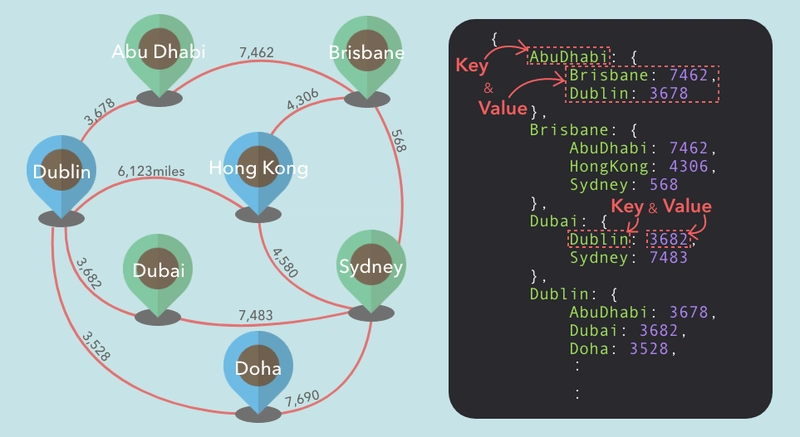
为了用 JavaScript 表示邻接表，我们可以使用键值对哈希表。每个键值对描述图中顶点的邻居集合。

使用邻接表存储图

假设我们想用一个图来表示航班连接。使用哈希表来绘制它，我们可以将机场名称存储为键。我们可以在它们的值中嵌套另一个哈希表，并使用目的地作为键，航班距离/（或费用）作为值。

基本实现

添加顶点和边

现在，让我们开始编码吧！首先，我们将创建 WeightGraph 类来初始化一个新对象。

class WeightedGraph {
    constructor() {
        this.adjacencyList = {};
    }
    addVertex() {
    }
    addEdge() {
    }
    removeEdge() {
    }
    removeVertex() {
    }
    DFS() {
    }
    BFS() {
    }
    Dijkstra() {
    }
}

然后，实现addVertex方法来创建没有任何连接的顶点，以及addEdge方法来创建两个顶点之间的无向边。

    constructor() {
        this.adjacencyList = {};
    }
    addVertex(name) {
        if (!this.adjacencyList[name]) {
            this.adjacencyList[name] = {};
        }
    }
    addEdge(vert1, vert2, weight) {
        this.adjacencyList[vert1][vert2] = weight;
        this.adjacencyList[vert2][vert1] = weight;
    }

如果我们想要使用此 addEdge 方法获取有向边，我们只需要删除最后一行this.adjacencyList[vert2][vert1] = duration;。

邻接表和每个顶点都是哈希表，因此添加顶点/边的时间复杂度为O(1)。

移除边和顶点

在无向图中，边由顶点的两侧指定。因此，如果我们想完全删除一条边，我们需要从两侧删除它们。

    removeEdge(v1,v2) {
        delete this.adjacencyList[v1][v2];
        delete this.adjacencyList[v2][v1];
    }

当我们从图中删除一个顶点时，我们需要确保删除与该顶点相连的边。我们可以使用 removeEdge 函数来实现这一点。

    removeVertex(vert) {
        for (let i in this.adjacencyList[vert]) {
            this.removeEdge(vert, i);
        }
        delete this.adjacencyList[vert];
    }

删除边需要O(1)常数时间。然而，删除顶点需要O(|E|)，这意味着它取决于其边的长度。

遍历（访问每个顶点）

现在我们将创建函数来遍历图。我们的目标是逐个访问所有顶点，但在图的遍历中，可能需要多次访问某些顶点。为了尽可能减少重复访问顶点的次数，有必要记录哪些顶点已经被访问过。

遍历图基本上有两种算法——深度优先搜索和广度优先搜索。

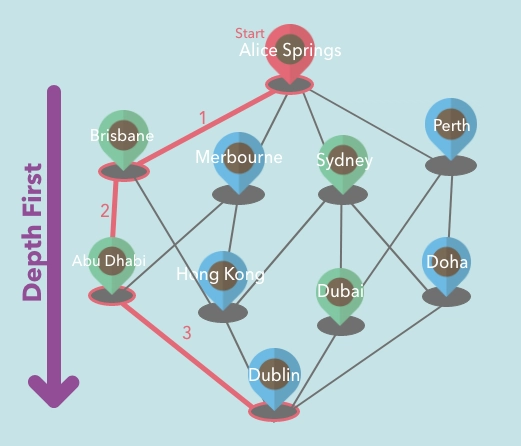
深度优先搜索

使用 DFS（深度优先搜索的缩写），我们会先访问邻居（子）顶点，然后再访问兄弟顶点。因此，如果我们将起始顶点放在图的顶部，我们就会直接到达图的底部。

执行：

    DFS(target) {
        const result = [];
        const visited = {};
        const helper = (vert) => {
            if (!vert) return null;
            visited[vert] = true;
            result.push(vert);
            for (let neighbor in this.adjacencyList[vert]) {
                if (!visited[neighbor]) {
                    return helper(neighbor)
                }
            }
        }
        helper(target);
        return result;
    }

我们在辅助函数中使用了递归。如果目标的邻居不在已访问列表中，则访问该邻居并将其指定为目标。对其邻居执行相同操作，并重复此操作，直到已访问列表中没有可添加的邻居为止。

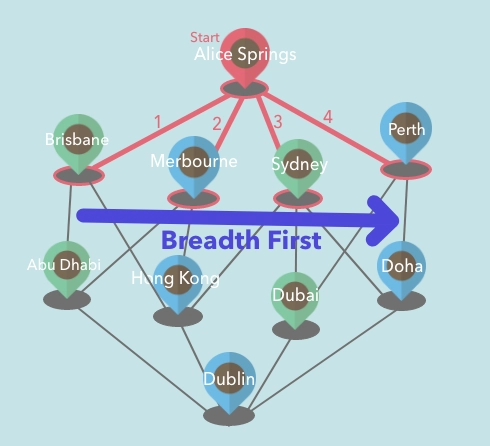
广度优先搜索

使用广度优先搜索 (BFS)，我们先访问兄弟顶点，然后再访问邻居（子）顶点。因此，如果我们从图的顶部顶点开始，我们首先遍历起始顶点的所有邻居。

执行：

    BFS(start) {
        const queue = [start];
        const result = [];
        const visited = {};
        while(queue.length) {
            let current = queue.shift();
            visited[current] = true;
            result.push(current)
            for (let neighbor in this.adjacencyList[current]) {
                if (!visited[neighbor]) {
                    visited[neighbor] = true;
                    queue.push(neighbor);
                }
            }
        }
        return result;
    }

在使用与 DFS 相同的访问列表的同时，我们还记录了在“队列”数组中访问下一个的位置。

寻找最短路径（Dijkstra算法）

我们会遇到很多情况，想要找出图中从一个点到另一个点的最短路径。

假设我们创建了一家在线旅行社，并有一个城市图谱，其中包含我们提供的往返这些城市的特价航班。我们的目标是为用户提供从他们所在城市到目的地的最便宜路线。然而，由于没有任何函数可以计算最便宜的路线，我们需要手动提取所有可能的路线并进行比较——这既耗时又费力。

迪杰斯特拉算法是艾德斯杰·迪杰斯特拉（Edsger W. Dijkstra）64年前为解决这个问题而构想的方法。

Dijkstra 算法的工作原理

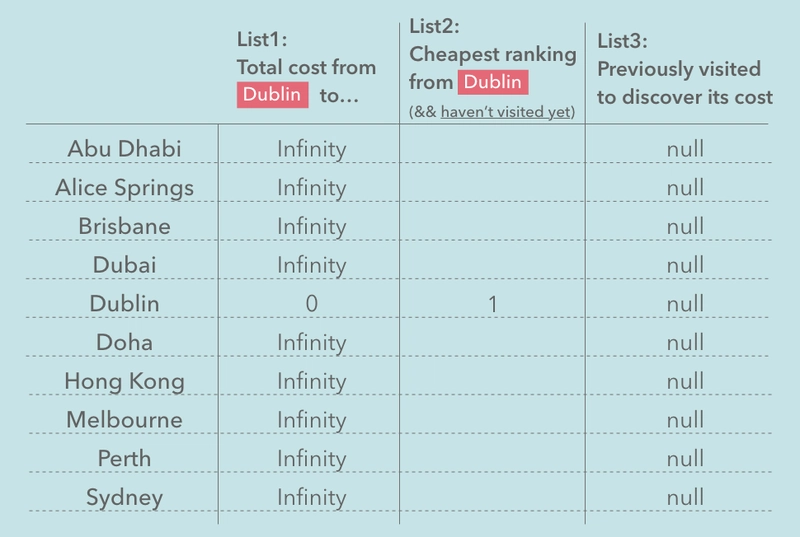
我们需要三个存储来跟踪主要信息：

所有机场的列表，以及从出发机场出发的总费用。
这份列表会告诉您哪条航线迄今为止的总费用最便宜 - 而且还会告诉您我们下一步应该访问哪个机场。
所有机场的列表，以及我们之前访问过哪个机场到达该机场的记录。

基本上这就是我们需要记录的全部内容，并且随着算法的进行，所有这些都会更新。

初始化

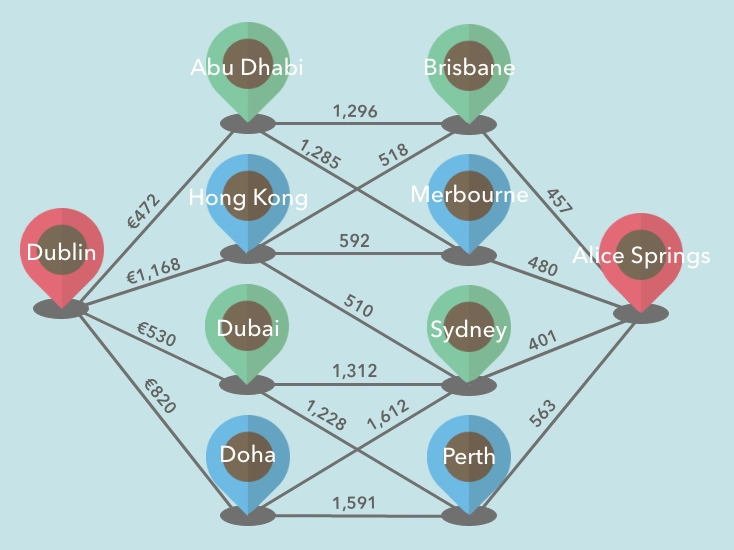
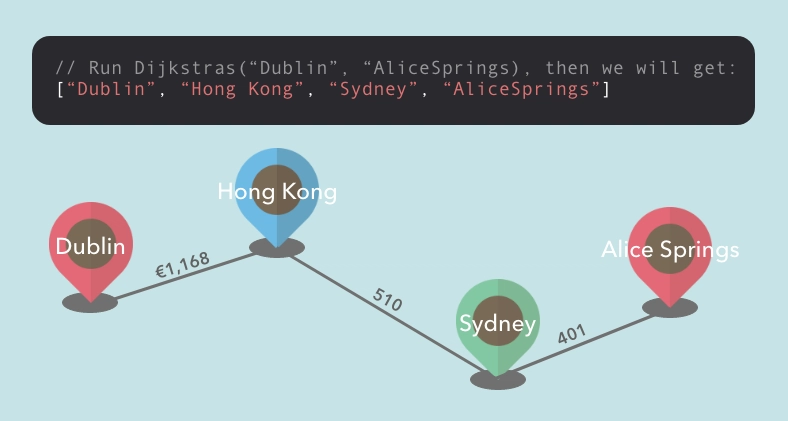
假设我们要找到从都柏林到爱丽丝泉的最便宜路线。因此，我们可以将航班成本指定为边的权重。

我们用图表来绘制它。

// console.log
{
    AbuDhabi: {
        Brisbane: 1296,
        Melbourne: 1285
    },
    AliceSprings: {
        Brisbane: 457,
        Melbourne: 480,
        Perth: 563,
        Sydney: 401
    },
    Brisbane: {
        AbuDhabi: 1296,
        HongKong: 518
    },
       .
       .
       .
    Sydney: {
        AliceSprings: 401,
        Dubai: 1312,
        Doha: 1612,
        HongKong: 510
    }
}

除了从都柏林到都柏林的总费用为 0之外，我们目前还不知道任何用于分配列表的信息。其余机场，我们将进行分配Infinity，以便无论何时发现新的费用，它都会比初始化时更便宜。

现在我们可以分配 List2，它会告诉您成本最低的路线——因为我们为从都柏林到都柏林的路线分配了零，这是迄今为止最便宜的路线。

代码中的初始化

现在让我们在代码中初始化这些列表。首先，我们将创建 Priority Queue 类来组织 List2——这个列表会告诉你当前哪条路线的总费用最低。

class PriorityQueue {
    constructor(){
        this.values = [];
    }
    enqueue(val, priority) {
        this.values.push({val, priority});
        this.sort();
    };
    dequeue() {
        return this.values.shift();
    };
    sort() {
        this.values.sort((a, b) => a.priority - b.priority);
    };
}

分配的最小数字priority将位于队列的开头。

接下来，我们创建接受起始顶点和最后一个停止顶点的 Dijkstra 算法函数。

    Dijkstras(start, finish) {
        // List1
        const costFromStartTo = {};
        // List2
        const checkList = new PriorityQueue();
        // List3
        const prev = {};

        let current;
        let result = [];
        for (let vert in this.adjacencyList) {

        }
        while (checkList.values.length) {

        }
    }

在里面，我们创建了三个列表来保存记录。

List1用于保存所有顶点，每个顶点的数值代表从起始顶点到目标顶点的总成本。我们将其命名为costFromStartTo。
List2是我们之前实现的优先级队列。我们称之为checkList——因为这个队列会告诉您接下来需要检查哪个顶点。
List3是所有顶点的列表，用于记录之前访问过的顶点，从而确定其当前成本。因此我们称之为prev。

shortest稍后将result在 while 循环中使用。

在 for 循环中，我们将用零和无穷大填充列表，这就是我们对起点和其余顶点的全部了解。

        let current;
        let result = [];
        for (let vert in this.adjacencyList) {
            if (vert === start) {
                costFromStartTo[vert] = 0;
                checkList.enqueue(vert, 0);
            } else {
                costFromStartTo[vert] = Infinity;
            }
            prev[vert] = null;
        }

如果我们Dijkstras("Dublin", "AliceSprings");现在运行，所有列表都应该像这样填充：

计算更新`costFromStartTo`列表

我们基本上要做的是不断计算以更新costFromStartTo列表。由于我们已经计算了从起点到相同起点的代价，我们可以查看与起始顶点相邻的顶点。现在我们可以计算它们从起始顶点到终点的总代价。

要在代码上执行此操作：

        for (let vert in this.adjacencyList) {
            .
            .
            .
        }
        while (checkList.values.length) {
            current = checkList.dequeue().val;
            for (let neighbor in this.adjacencyList[current]) {

            }
        }

我们选择检查与当前拥有最便宜总成本的顶点相邻的顶点。

要找出总成本最低的顶点，我们只需查看中的第一个顶点即可checkList。同时，我们可以将其从列表中删除，这样只要没有新的更便宜的路线更新，该顶点就不会再次被访问。

然后，我们可以循环遍历每个连接的顶点，并在计算每个成本时更新三个列表。

        while (checkList.values.length) {
            current = checkList.dequeue().val;
            for (let neighbor in this.adjacencyList[current]) {
                let costToNeighbor = costFromStartTo[current] + this.adjacencyList[current][neighbor];
                if (costToNeighbor < costFromStartTo[neighbor]) {
                    costFromStartTo[neighbor] = costToNeighbor;
                    prev[neighbor] = current;
                    checkList.enqueue(neighbor, costToNeighbor);
                }
            }
        }

我们将从起始点到当前顶点的花费，以及从当前顶点到邻居的单独花费相加。如果总和小于costFromStartTo邻居节点列表上的当前花费，我们就用总和更新列表。

我们还会进行更新prev[neighbor] = current，以记住哪条路线最便宜，可以到达邻居。

此时，我们还需要将邻居添加到中CheckList。在中分配所有邻居后CheckList，您就知道哪个邻居目前最便宜。这也意味着它目前到达最后一站的可能性最高。

现在，我们只需要循环这个过程，直到到达优先级队列开头的最后一站visitedList。

        while (checkList.values.length) {
            current = checkList.dequeue().val;
            if (current === finish) {
                // Done
                while (prev[current]) {
                    result.push(current);
                    current = prev[current];
                }
                break;
            }
            else {
                for (let neighbor in this.adjacencyList[current]) {
                    let costToNeighbor = costFromStartTo[current] + this.adjacencyList[current][neighbor];
                    if (costToNeighbor < costFromStartTo[neighbor]) {
                        costFromStartTo[neighbor] = costToNeighbor;
                        prev[neighbor] = current;
                        checkList.enqueue(neighbor, costToNeighbor);
                    }
                }
            }
        }
        return result.concat(current).reverse();

当我们从 checkList 中提取最后一个停止点时，我们可以停止所有程序——因此我们创建 if 语句来完成循环，并用 else 语句包装程序以更新列表。

最后，我们反转结果列表并返回它。

结论

如果我们想要表示数据之间的复杂联系，图（Graph）可能是一个合适的数据结构。换句话说，如果节点之间没有影响决策的联系，我们就不需要使用图。因此，回到第一个问题——我们是否要实现图来组织词汇表？或许最好的选择是坚持使用简单的哈希表，因为我们不需要呈现词汇表之间的特定联系。

非常感谢你的阅读！如果你有任何想法，或者想改进代码，请留言，我会非常感激你的反馈。:)

资源

Colt Steele 主讲的 JavaScript 算法和数据结构大师课 - Udemy
Graph（抽象数据类型）- 维基百科

文章来源：https://dev.to/maikomiyazaki/completed-javascript-data-struct-course-and-here-is-what-i-learned-about-graph-dijkstra-algorithm-57n8

完成了 JavaScript 数据结构课程，以下是我学到的关于图（+ Dijkstra 算法）的知识。首先，什么是图？如何用 JavaScript 实现图？基本实现：查找最短路径（Dijkstra 算法） 结论：资源

完成了 JavaScript 数据结构课程，以下是我学到的关于图形（+ Dijkstra 算法）的知识。

首先，什么是Graph？

我们如何使用 JavaScript 实现图表？

基本实现

寻找最短路径（Dijkstra算法）

结论

资源

首先，什么是Graph？

两种类型的图表

加权/非加权图

我们如何使用 JavaScript 实现图表？

使用邻接表存储图

基本实现

添加顶点和边

移除边和顶点

遍历（访问每个顶点）

深度优先搜索

广度优先搜索

寻找最短路径（Dijkstra算法）

Dijkstra 算法的工作原理

初始化

代码中的初始化

计算更新costFromStartTo列表

结论

资源

完成了 JavaScript 数据结构课程，以下是我学到的关于图（+ Dijkstra 算法）的知识。首先，什么是图？如何用 JavaScript 实现图？基本实现：查找最短路径（Dijkstra 算法）结论：资源

计算更新`costFromStartTo`列表