读取高效数据结构
介绍
最小化读取开销
哈希表
红黑树
跳过列表
比较
参考
介绍
上一篇文章介绍了 RUM 猜想。它描述了在设计数据结构和访问方法时应该考虑的读取 (RO)、更新 (UO) 和内存 (MO) 开销之间的权衡。
在本文中,我们将深入探讨一些在实践中常用的低读取开销数据结构,例如哈希表、红黑树和跳过列表。本篇博文是 RUM 系列的第二篇:
为了比较不同的实现,我们使用与上一篇文章相同的示例。任务是实现一组整数,这次重点关注少量的读取开销。
这篇文章的结构如下。第一部分,我们想回顾上一篇文章中读取开销最小的解决方案。接下来的部分将深入探讨三种实用的替代方案,首先是哈希表,然后是红黑树,最后是跳过列表。最后一部分将从理论角度比较这三种不同的数据结构,并进行一些简单的运行时实验来总结。
最小化读取开销
我们已经看到了读取开销方面的最佳实现:给定从 0 到 1000 的可能整数,我们可以利用一个a大小为 的布尔数组1001。数组元素用 初始化false。为了将整数标记i为集合的成员,我们将其设置为a[i] := true。回想一下以下开销:
- 反渗透 = 1
- 铀=1
- 分子轨道 → ∞
对于大多数实际场景来说,这都是不切实际的,因为内存开销会随着可能值的数量而增长。虽然理论上可以将此方法用于整数,但例如,如果我们尝试将字符串存储在集合中,则无法实现。如何在不损失太多读取(和写入)性能的情况下降低内存开销?
实际上,这是通过使用哈希、排序树或基于列表的方法来实现的。让我们来看看三种旨在提高读取效率且不会牺牲太多写入和内存性能的数据结构:哈希表、红黑树和跳过列表。
哈希表
概念
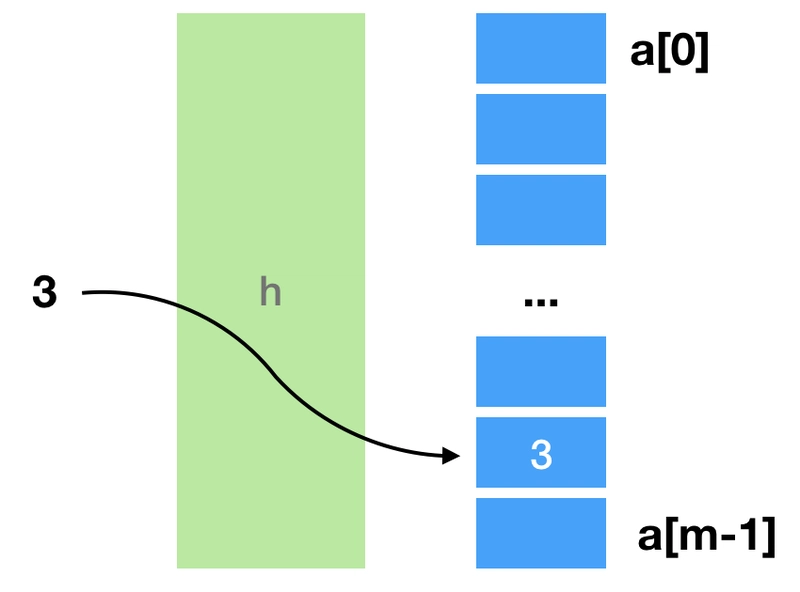
哈希表的思想与最优解中的类似。我们不是为每个可能的整数预留一个布尔值槽,而是将空间限制为一个大小为m的整数数组a。然后,我们选择一个函数h,使得对于每个整数i : h(i) ∈ [0..m-1]。该函数可用于计算数组索引,并将i存储在 中。a[h(i)]
下图说明了整数 3 是如何存储在使用哈希表实现的集合中的。我们计算h(3)并将其值存储在数组的相应字段中。
我们如何选择h?对于h ,一个实际的选择是重用现有的加密哈希函数(例如MD5),并将结果值对m取模。缺点是这些哈希函数可能很慢。这就是为什么 Java 依赖于针对每种数据类型(例如 )的自定义哈希函数String。
如果我们预先知道所有可能的值,就可以选择一个完美的哈希函数。但大多数情况下这是不可能的。如果两个整数i和j映射到同一个索引h(i) = h(j),我们该怎么办?目前有多种技术可以解决这些所谓的冲突。
一种冲突解决方法是分离链接。在分离链接中,我们不将实际值存储在数组中,而是存储在另一层数据结构中。首先计算数组索引,然后查询存储在那里的数据结构,从哈希表中读取值。可能的候选结构是基于树或列表的结构,如下节所述。但如果预计冲突次数较少,通常也只使用链表。
另一种常用的方法称为开放寻址。如果发生碰撞,我们会根据某种探测策略计算一个新的索引,例如使用h(i) + 1进行线性探测。
RUM 开销
哈希表实现的 RUM 开销很大程度上取决于所选的哈希函数、数组大小m以及冲突解决策略。这使得调整哈希表的 RUM 开销成为可能。
如果没有冲突,读取开销仅受计算h(i)的开销影响。计算哈希函数的开销越小,总体读取开销就越小。如果发生冲突,则会产生额外的开销,具体取决于解决策略。虽然选择一个近乎完美的哈希函数来避免冲突是有用的,但如果我们让哈希函数足够快,并在解决冲突时允许一些额外的操作,总开销可能会更小。
由于更新需要先进行读取操作,因此更新开销等于读取开销,再加上对数组或链接数据结构(如果是单独链接)的插入/删除操作。
内存开销与负载因子( n/m )间接成正比。如果我们使用单独的链接来解决冲突,还必须考虑额外的内存。
如果我们插入越来越多的数据,内存开销就会减少。然而,由于我们必须解决更多的冲突,读取开销会增加。在这种情况下,可以重新缩放哈希表,这需要将现有数据完整复制到更大的数组中,并重新计算所有哈希值。
渐近复杂性
读取和更新操作的平均渐近复杂度为常数,因为计算哈希值所需的时间是常数,与表中存储的数据量无关。在最坏情况下(所有n 个输入值都获得相同的哈希值),我们需要解决n - 1 个冲突。因此,最坏情况下的性能与将数据存储在无序数组中并执行全表扫描的性能一样差。如果m尽可能小,并且根据需要调整哈希表的大小,则摊销后的内存需求与集合中存储的值数量呈线性关系。
| 类型 | 平均的 | 最坏的情况 |
|---|---|---|
| 读 | O(1) | 在) |
| 更新 | O(1) | 在) |
| 记忆 | 在) | 在) |
基于哈希表的数据结构的读取性能平均而言是恒定的。然而,由于其设计,它仅高效地支持点查询。如果您的访问模式包含范围查询,例如检查集合中是否包含整数[0..500],则哈希集并非理想之选。为了高效地支持范围查询,我们可以将数据以排序的方式存储。二叉搜索树是此用例最常见的数据结构类型之一。
红黑树
概念
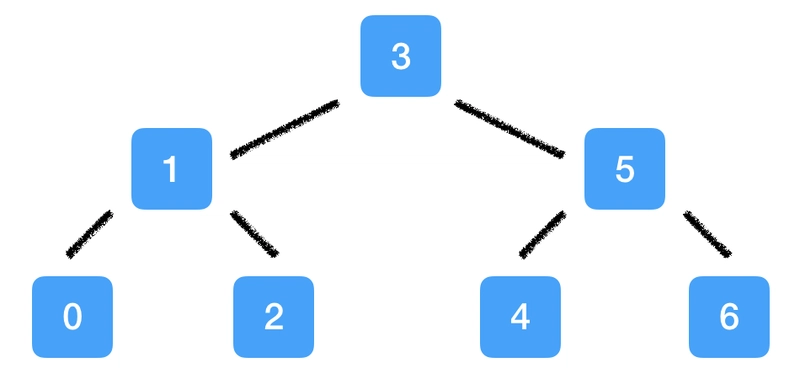
在二叉搜索树中,数据存储在节点中。每个节点最多有两个子节点。左子树仅包含小于当前节点的元素。右子树仅包含大于当前节点的元素。如果二叉搜索树是平衡的,即对于所有节点,左子树和右子树的高度最多相差 1,则搜索节点所需的时间是对数级的。下图演示了如何在二叉搜索树中存储集合{0..6} 。
问题是,在插入和删除元素时,如何保持树的平衡?我们需要相应地设计插入和删除算法,使树实现自平衡。红黑树 [1] 是这种自平衡二叉搜索树的一个广泛使用的变体。
在红黑树中,每个节点除了存储实际值之外,还存储其颜色。插入或删除节点时会使用颜色信息来确定如何重新平衡树。重新平衡是通过更改颜色并递归地围绕父节点旋转子树来完成的,直到树再次达到平衡。
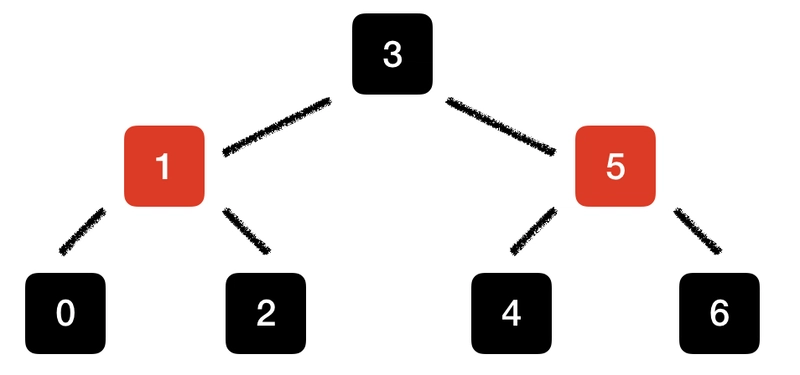
详细解释该算法超出了本文的范畴,所以请自行查阅相关资料。此外,David Galles 还制作了一篇精彩的红黑树交互式可视化图,值得一看。现在,我们来看看存储在红黑树中的同一个示例集合{0..6} 。
需要注意的是,红黑树并不一定完全平衡,而是根据子树中黑色节点的高度来判断。由于红黑树的不变量,平衡的红黑树永远不会比完全平衡的红黑树差太多,也就是说,它们在搜索时具有相同的渐近复杂度。
RUM 开销
自平衡二叉搜索树的 RUM 开销取决于保持树平衡的算法。在红黑树中,重新平衡以递归方式进行,并且可能影响一直到根节点的节点。
读取操作需要遍历树,直到找到元素。如果元素存储在叶节点中,则最多需要log(n) + c 个遍历步骤,其中c是树非完美平衡时的潜在开销。
与基于哈希表的实现一样,对基于红黑树的集合进行更新操作首先需要执行读取操作。除了读取开销之外,更新开销还取决于要更新的值、是否应该插入或移除该值,以及树的当前结构。在最简单的情况下,更新只需要对父节点进行一次操作,即修改指向子节点的指针。最坏的情况是,我们必须重新平衡树,直至根节点。
渐近复杂性
由于红黑树是平衡树,读取操作具有对数复杂度,因此搜索值在概念上相当于二分查找。更新操作具有相同的复杂度,因为它们需要对数搜索,加上最坏情况下从叶节点到根节点的重新平衡操作,这同样是对数复杂度。由于每个值需要一个节点,因此内存需求是线性的。
| 类型 | 平均的 | 最坏的情况 |
|---|---|---|
| 读 | O(log n) | O(log n) |
| 更新 | O(log n) | O(log n) |
| 记忆 | 在) | 在) |
我们已经看到,如果需要范围查询或需要以排序的方式向用户呈现数据,自平衡二叉搜索树是一种非常有用的数据结构。然而,使其自平衡所需的算法相当复杂。此外,如果我们想要支持并发访问,我们必须在重新平衡期间锁定树的某些部分。如果需要进行大量的重新平衡操作,这可能会导致不可预测的缓慢速度。
我们如何设计一个并发友好的数据结构,同时支持对数搜索成本?
跳过列表
概念
链表的设计使其非常适合并发操作,因为更新操作高度本地化且缓存友好 [3]。如果我们的数据是有序序列,我们可以使用二分查找来实现对数级的读取复杂度。然而,有序链表的问题在于我们无法访问链表中的随机元素。因此,二分查找是不可能的。或者说,二分查找真的可行吗?这时,跳跃表就派上用场了。
跳过列表是平衡树的概率替代方案 [4, 5, 6]。跳过列表的核心思想是使用跳过指针为数据的后续部分提供快速通道。
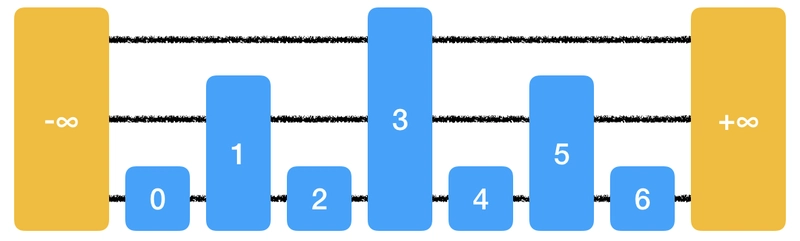
要执行二分查找,我们必须将查询与中位数进行比较。如果中位数不是我们要查找的元素,则取左子列表或右子列表,并递归地重复中位数比较。这意味着我们实际上不需要完全随机访问,而是访问当前子列表的中位数。下图说明了如何使用跳跃指针实现这一点。
这个跳跃表有三层。最底层包含整数{0..6}的完整集合。下一层只包含{1, 3, 5},而上一层只包含{3}。我们添加了两个人工节点-∞和∞。每个节点包含一个值和一个指针数组,每个指针指向相应层级上的后继节点。如果我们现在想检查4是否是该集合的成员,请按以下步骤操作。
- 从最左边的元素(-∞)开始,指向最上面的指针(级别 3)
- 将查询 ( 4 ) 与当前级别中的下一个元素 ( 3 )进行比较
- 由于3 < 4,我们向右移动一个元素(到3)
- 然后,我们再次将查询 ( 4 ) 与当前级别中的下一个元素 ( ∞ )进行比较
- 当∞ >= 4 时,我们向下移动一级(至第 2 级)
- 然后,我们再次将查询 ( 4 ) 与当前级别中的下一个元素 ( 5 )进行比较
- 由于5 >= 4,我们向下移动一级(至 1 级)
- 然后,我们再次将查询 ( 4 ) 与当前级别中的下一个元素 ( 4 )进行比较
- 由于4 = 4,查询成功返回
如果列表是静态的,并且我们可以构建跳跃指针来支持二分查找,那么此算法会非常有效。然而,在实际场景中,我们希望能够插入或删除元素。如何才能高效地支持插入和删除操作,同时又不失去跳跃指针良好放置的良好特性?每次修改后都完全重建跳跃列表是不切实际的。最终,我们希望实现高度本地化的更新,以支持高并发性。
我们引入了跳跃表作为平衡树的概率替代方案。而概率部分正是解决跳跃指针在何处以及如何放置的问题所需要的。
对于每个想要插入跳跃表的元素,我们首先搜索它在现有元素中的位置。然后将其插入到最低层。之后,我们抛硬币。如果硬币反面朝上,则完成。如果正面朝上,则将该元素“提升”到下一层,将其插入到更高层的列表中,并重复该过程。要删除一个元素,我们先搜索它,然后将其从所有层级中移除。欢迎查看这个精彩的交互式跳跃表可视化效果。
由于插入算法的不确定性,实际的跳过表看起来并不像上图那样最优。它们很可能看起来更加混乱。尽管如此,可以证明预期搜索复杂度仍然是对数级的 [7]。
RUM 开销
跳过列表中的 RUM 开销是不确定的。这也是渐近复杂度分析比通常更复杂的原因,因为它也涉及概率论。不过,我们将从概念层面来探讨不同的开销。
读取操作需要遍历一系列水平和垂直指针,并将查询结果与沿途的不同列表元素进行比较。这意味着在查询返回之前,可能需要进行大量的辅助读取。
你可能已经猜到了,我们需要先执行读取操作才能执行更新。辅助更新(即提升)的数量是不确定的。然而,它们完全是本地的,不依赖于剩余跳跃表的结构。这使得并行化更新变得容易。
内存开销取决于晋升的数量,因为我们必须为每次晋升存储额外的指针。通过使用非公平硬币,即使用晋升/不晋升的概率[p, 1-p](0 < p < 1而不是[0.5, 0.5]),我们实际上可以调整内存开销,潜在地抵消额外的读取和更新开销。如果我们选择p = 0,我们将得到一个链表,它具有我们可以在此数据结构中实现的最小内存开销。如果我们选择的p太大,我认为内存和读取开销都会增加,因为我们可能不得不沿着不同级别执行大量垂直移动。
渐近复杂性
分析跳跃表的渐近复杂度有多种方法。两种常用的方法是查看预期渐近复杂度或高概率成立的渐近复杂度。为了简单起见,我们在这里只讨论预期复杂度。
如上所述,在实现跳过列表时,存在极小的可能性导致元素无限提升。虽然预期层级数为O(log(n)),但理论上是无界的。为了解决这个问题,可以设定元素最多可以提升的层级数M。如果M足够大,在实践中不会产生负面影响。
平均情况下,预期读取和更新复杂度呈对数关系。跳过列表的预期高度为O(log(n))。然而,提升元素高度的可能性较小,这使我们能够推导出线性预期内存需求 [8]。
对于有界列表,分析最坏情况更有趣,因为无界最坏情况是无限高的跳跃列表。在有界列表的最坏情况下,我们将每个元素提升到最高层。如果我们选择最高层依赖于n,就可以推导出读取和更新操作的线性复杂度。
| 类型 | 平均的 | 最坏情况(M界) | 最坏情况(无界) |
|---|---|---|---|
| 读 | O(log n) | 在) | ∞ |
| 更新 | O(log n) | 在) | ∞ |
| 记忆 | 在) | O(纳摩尔) | ∞ |
现在,我们了解了业界广泛使用的三种不同类型的数据结构。我们从理论的角度逐一分析了它们。下一节将进行静态比较,总结我们的发现,并使用 Java 标准库中的实现进行一些运行时实验。
比较
理论比较
从我们今天所学的知识来看,可以肯定地说,读取高效的数据结构旨在实现亚线性读取开销。哈希表非常适合内存中的映射或集合。其缺点在于,如果数据增长,需要重新缩放底层数组,并且缺乏范围查询支持。如果关注范围查询或排序输出,基于树的数据结构是一个不错的选择。跳跃表有时比树更受欢迎,因为它更简单,尤其是在无锁实现方面。
一些数据结构可以根据 RUM 开销进行配置。通过调整冲突解决策略或所需的负载因子等参数,我们可以在哈希表中权衡内存开销和读取开销。在跳过列表中,我们可以通过修改提升概率来实现这一点。
下表总结了我们在本文中看到的三种数据结构的平均渐近读取、更新和内存要求,以及 RUM 可调整性方面。
| 哈希表 | 红黑树 | 跳过列表 | |
|---|---|---|---|
| 平均阅读量 | O(1) | O(log n) | O(log n) |
| 平均更新 | O(1) | O(log n) | O(log n) |
| 平均内存 | 在) | 在) | 在) |
| RUM调整参数 | 负载因子、哈希函数、碰撞解决策略 | - | 晋升概率 |
运行时实验
最后但同样重要的一点是,我们要看一下三个 Java 标准库数据结构的实际读取性能:HashSet、TreeSet和ConcurrentSkipListSet。
HashSet使用单独的链接来解决冲突。如果存储桶中的元素数量足够少,它们将被存储在列表中。如果数量超过TREEIFY_THRESHOLD,它将被迁移到红黑树。TreeSet使用红黑树实现。 和HashSet都不TreeSet是线程安全的,也不支持并发修改。顾名思义,ConcurrentSkipListSet支持并发访问。基础列表使用 Harris-Maged 链接有序集算法的变体 [9, 10]。
作为基准,我们用n 个随机整数生成一个集合,并将其分别复制到HashSet、TreeSet和中。我们还用这些数字创建了一个读取最优集合,即使用一个巨大的布尔数组。然后,我们创建一个包含n 个ConcurrentSkipListSet随机点查询的列表,并测量所有查询完成的运行时间。
我们使用ScalaMeter来测量运行时性能。欢迎查看我的微基准测试博客文章,其中包含有关该工具的更多详细信息。
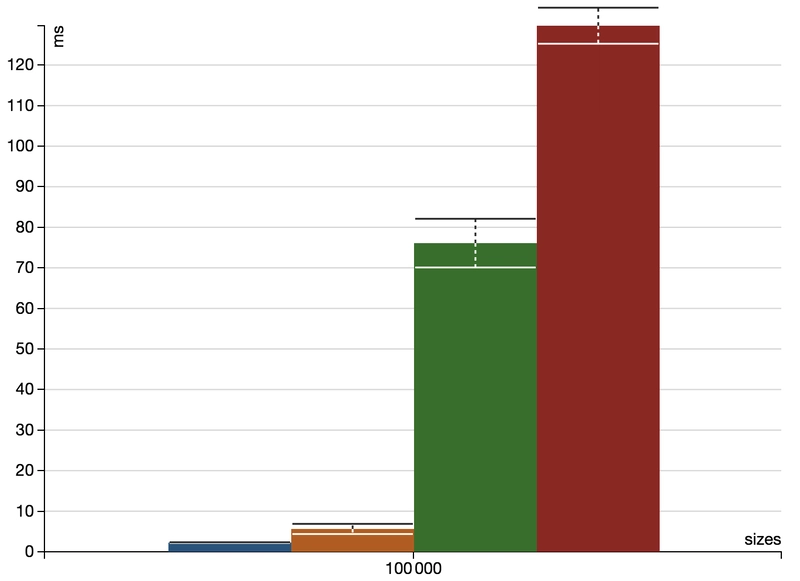
下图显示了对 100 000 个随机整数生成的不同集合进行 100 000 个点查询的运行时间。
正如预期的那样,读取优化实现的性能明显优于其他所有实现。哈希集位居第二。读取优化实现和哈希集都具有恒定的渐近读取开销。树集和跳跃列表集的性能要差得多。这也是意料之中的,因为它们具有对数级的运行时间复杂度。
看看这四种实现的其他开销,以及将并发性纳入其中,也很有趣。不过我把这个练习留给读者了 :P 在下一篇文章中,我们将深入探讨那些旨在降低更新开销的高效数据结构。
参考
- [1] Guibas, LJ 和 Sedgewick, R.,1978 年 10 月。《平衡树的二色框架》。载于《计算机科学基础》,1978 年第 19 届年度研讨会(第 8-21 页)。IEEE。
- [2]常见 Java 数据类型的内存消耗(第 2 部分),作者:Mikhail Vorontsov
- [3]选择并发友好的数据结构,作者:Herb Sutter
- [4] Pugh, W.,1989年8月。“跳过列表:平衡树的概率替代方案”。《算法与数据结构研讨会》(第437-449页)。Springer出版社,柏林,海德堡。
- [5] Fraser, K. 和 Harris, T.,2007.无锁并发编程。ACM 计算机系统学报(TOCS),25(2),第 5 页。
- [6] Herlihy, M.、Lev, Y.、Luchangco, V. 和 Shavit, N.,2006 年。《一个可证明正确的可扩展并发跳过列表》。在分布式系统原理会议 (OPODIS) 上。
- [7] Papadakis, T.,1993. 跳过列表和算法的概率分析。博士论文:滑铁卢大学。
- [8]跳过列表- 内盖夫本·古里安大学数据结构课程
- [9] Harris, TL,2001年10月。非阻塞链表的实用实现。国际分布式计算研讨会论文集(第300-314页)。Springer出版社,柏林,海德堡。
- [10] Michael,MM,2002年8月。高性能动态无锁哈希表和基于列表的集合。载于第十四届ACM并行算法与架构研讨会论文集(第73-82页)。ACM。
- 封面图片由 Smabs Sputzer - It's a Rum Do... 于 flickr 上提供,CC BY 2.0,https://commons.wikimedia.org/w/index.php? curid=59888481
如果您喜欢这篇文章,您可以在 ko-fi 上支持我。
文章来源:https://dev.to/frosnerd/read-efficient-data-structs-57i5 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com