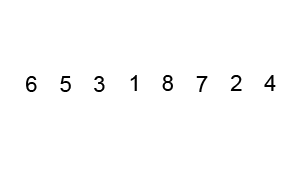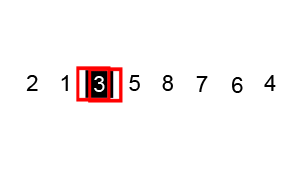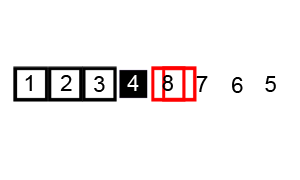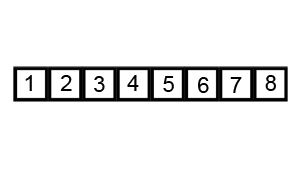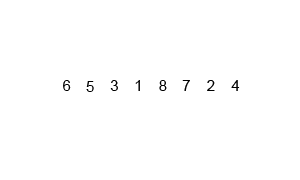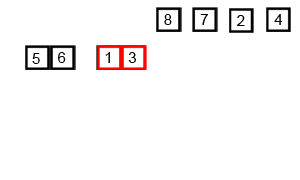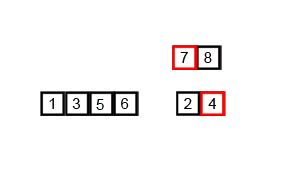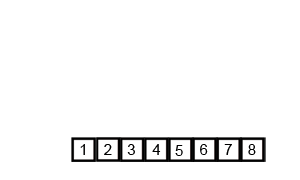8 个必须知道的排序算法

在这篇文章中，我将向你展示常见的排序算法，并提供它们的 Python 实现。
如果你是一名程序员，或者你已经参加过面试，那么你肯定知道了解和掌握算法对于提高你的编程水平或获得录用机会的重要性。
即使它们看起来很简单，但实际上也可能很棘手。

这就是为什么你应该多加练习。
正如一位智者在Quora上所说：

算法是用来练习的，而不是用来学习的。

我想你已经明白我的意思了，那我们就深入探讨一下吧。

排序算法

处理数据时，排序是必不可少的任务之一。尽管排序方法有很多，但有些方法比其他方法更好，有些方法则针对特定用途更高效。
根据所使用的方法（递归、迭代、比较）或数据结构，您可以拥有很多可能性。

8 个必须知道的排序算法

本节重点讲解每种算法：概念、复杂性和用例。我还提供了用 Python 编写的每种算法的解决方案，但如果您想挑战自己，请在检查之前先自行尝试一下。😉
冒泡排序
冒泡排序是一种简单的排序算法，如果元素顺序错误，则交换元素。
示例：

冒泡排序（来自WikiPedia）



    #Bubble Sort Algorithm

    def bubbleSort(data):
        lenght = len(data)

        for iIndex in range(lenght):
            swapped = False

            for jIndex in range(0, lenght - iIndex - 1):

                if data[jIndex] > data[jIndex + 1]:
                    data[jIndex], data[jIndex + 1] = data[jIndex + 1], data[jIndex]
                    swapped = True

            if swapped == False:
                break

        print(data)

冒泡排序的最坏和平均复杂度是 О(n2)，这意味着数据与我们想要排序的顺序相反，或者元素在列表中任意分布。
最佳情况的复杂度为 O(n)。这是数据已经排序的情况。

冒泡排序用于以下情况：

代码简洁优先；
复杂性并不重要。

选择排序
是冒泡排序的改进版本，因为它的性能更高。即使它们在最坏情况下的性能相同，选择排序的交换次数也更少。
选择排序有两种工作方式：要么在列表中查找最小项并将其放在列表的最前面（确保该项位于正确的位置）；要么查找最大项并将其放在列表的最后。
例如：

选择动画。红色表示当前分钟数。黄色表示排序列表。蓝色表示当前项目。维基百科
代码



    #Selection Sort Algorithm

    def selectionSort(data):

        for scanIndex in range(0, len(data)):

            minIndex = scanIndex

            for compIndex in range(scanIndex + 1, len(data)):
                if data[compIndex] < data[minIndex]:
                    minIndex = compIndex

            if minIndex != scanIndex:
                data[scanIndex], data[minIndex] = data[minIndex], data[scanIndex]

                print(data)

选择排序与冒泡排序具有相同的复杂性。
选择排序用于以下情况：

对小数组进行排序
必须勾选所有元素
需要更少的交换

插入排序
插入排序是一种强力排序算法，但它的比较次数比选择排序少。
插入排序的工作原理是选择一个元素，然后根据其直接邻居是否大于/小于所选元素进行排序。随着已排序元素数量的增加，算法会将新元素与已排序元素进行比较，并将新元素插入到列表中的正确位置。
示例：

图片来自维基百科
代码：



    #Insertion Sort Algorithm

    def insertionSort(data):

        for scanIndex in range(1, len(data)):
            tmp = data[scanIndex]

            minIndex = scanIndex

            while minIndex > 0 and tmp < data[minIndex - 1]:
                data[minIndex] = data[minIndex - 1]
                minIndex -= 1

            data[minIndex] = tmp

            print(data)

插入排序的最坏和平均复杂度情况均为 O(n²)。这分别发生在数组按逆序排序和元素在数组中任意排列时。
最佳复杂度为 O(n)。当数据已按所需顺序排序时，就会发生这种情况。

插入排序用于以下情况：

还剩下几个元素需要排序；
阵列很小。

快速排序
是一种高效的排序算法。它使用分治法将数组拆分成子数组，并递归调用这些子数组对元素进行排序。
实现快速排序算法需要选择一个基准，然后根据基准将数组拆分成两个子数组，如果它们大于/小于基准，则按顺序排列它们。然后，我们对这两个子数组进行排序，并重复该过程。
示例：

图片来自维基百科
代码：



    #Quick Sort Algorithm


    def quickSort(data, left, right):
        if right<= left:
            return 
        else:
            pivot = partition(data, left, right)
            quickSort(data, left, pivot - 1)
            quickSort(data, pivot + 1, right)

        return data

    def partition(data, left, right):
        """This function chooses a pivot point that dertermines the left and right side of the sort"""
        pivot = data[left]
        leftIndex = left + 1
        rightIndex = right

        while True:
            while leftIndex <= rightIndex and data[leftIndex] <= pivot:
                leftIndex += 1
            while rightIndex >= leftIndex and data[rightIndex] >= pivot:
                rightIndex -= 1
            if rightIndex <= leftIndex:
                break
            data[leftIndex], data[rightIndex] = data[rightIndex], data [leftIndex]
            print(data)

        data[left], data[rightIndex] = data[rightIndex], data[left]
        print(data)

        return rightIndex

快速排序的最坏情况复杂度为 O(n²)。当所选的枢轴元素始终是最大或最小元素时，就会发生这种情况。
最佳情况和平均情况的复杂度均为 O(n*log(n))。当枢轴元素始终是中间元素或接近中间元素时，就会发生这种情况。

快速排序用于以下情况：

需要并支持递归；
阵列较小；
还剩下几个元素需要排序。

归并排序

归并排序采用分治法。排序首先将数据集拆分成多个独立的部分，并对这些部分进行排序。然后，它会将这些部分合并，并确保合并后的部分也已排序。
排序和合并过程持续进行，直到整个数据集重新合并为一个整体。
示例：

合并排序的示例。首先将列表划分为最小单元（1 个元素），然后将每个元素与相邻列表进行比较，对两个相邻列表进行排序和合并。最后，对所有元素进行排序并合并。维基百科
代码：



    #Merge Sort Algorithm

    def mergeSort(data):
        """This function determines whether the list is broken
            into individual parts"""

        if len(data) < 2:
            return data

        middle = len(data)//2

        # We break the list in two parts
        left = mergeSort(data[:middle])
        right = mergeSort(data[middle:])

        # Merge the two sorted parts into a larger piece.

        print("The left side is: ", left)
        print("The right side is: ", right)

        merged = merge(left, right)

        print("Merged ", merged)
        return merged
    def merge(left, right):
        """When left side/right side is empty, 
        It means that this is an individual item and is already sorted."""

        #We make sure the right/left side is not empty
        #meaning that it's an individual item and it's already sorted.
        if not len(left):
            return left

        if not len(right):
            return right

        result = []
        leftIndex = 0
        rightIndex = 0
        totalLen = len(left) + len(right)

        #
        while (len(result) < totalLen):

            #Perform the required comparisons and merge the two parts

            if left[leftIndex] < right[rightIndex]:
                result.append(left[leftIndex])
                leftIndex += 1
            else:
                result.append(right[rightIndex])
                rightIndex += 1

            if leftIndex == len(left) or rightIndex == len(right):
                result.extend(left[leftIndex:] or right[rightIndex:])

                break

        return result

MergeSort 的最坏情况和平均情况复杂度为 O(n*log(n))，这使得它比其他一些排序算法更快。

桶排序
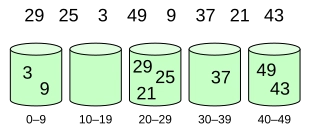
桶排序算法的工作原理是将数组划分为桶。然后，使用任意排序算法或递归调用桶排序算法对每个桶中的元素进行排序。
桶排序的过程可以理解为一种分散-聚集方法。首先，将元素分散到桶中，然后对桶中的元素进行排序。最后，按顺序将元素聚集在一起。
示例：

代码：



    #Bucket Sort Algorithm

    def bucketSort(data):
        bucket = []

        for iIndex in range(len(data)):
            bucket.append([])

        for jIndex in data:
            index_bucket = int(10 * jIndex)
            bucket[index_bucket].append(jIndex)
            print(bucket)

        for iIndex in range(len(data)):
    #I used the built-in method sorted() to sort the array. 
            bucket[iIndex] = sorted(bucket[iIndex])

            kIndex = 0

            for iIndex in range(len(data)):

                for jIndex in range(len(bucket[iIndex])):
                    data\[kIndex] = bucket[iIndex\][jIndex]
                    kIndex += 1

        print(data)

桶排序算法的最坏情况复杂度为 O(n²)。当同一范围内的元素被放入同一个桶中时，就会发生这种情况，导致某些桶中的元素比其他桶中的元素多。此外，如果使用不合适的排序算法对桶中的元素进行排序，情况可能会更糟。
最佳复杂度为 O(n+k)。当元素均匀分布在各个桶中，且每个桶中的元素数量基本相等时，最佳复杂度就会出现。如果数组已经排序，则复杂度会更高。
平均复杂度为 O(n)。当元素在数组中随机分布时，就会发生这种情况。

桶排序用于以下情况：

使用浮点数；
输入在一定范围内均匀分布。

希尔排序
是插入排序的一种变体。在该算法中，数组会根据所选序列按特定间隔进行排序。元素之间的间隔会根据所选序列逐渐减小。希尔排序的性能取决于给定输入数组所使用的序列类型。
例如：

GfyCat代码中的 Gif
：



    #Shell Sort Algorithm

    def shellSort(data, length):

        gap = length//2

        while gap > 0:
            for iIndex in range(gap, length):

                temp = data[iIndex]

                jIndex = iIndex

                while jIndex >= gap and data[jIndex - gap] > temp:
                    data[jIndex] = data[jIndex - gap]

                    jIndex -= gap

                data[jIndex] = temp

            gap //= 2

        print(data)

希尔排序的最坏情况复杂度小于或等于 O(n2)。
希尔排序的平均情况和最佳情况复杂度为O(n*log(n))。
希尔排序适用于以下情况：
递归超出限制。
当近距离元素较远时，插入效果不佳。

堆排序
堆排序是最好的排序方法之一，因为它可以就地进行，并且没有二次最坏情况复杂度。堆排序使用堆数据结构。
堆是一个完全二叉树。它还验证以下规则：

孩子比父母小；
最大/最小元素位于堆的根，取决于您对其进行排序的方式。

要编写堆排序算法，我们必须先创建一个数组的堆。完成后，我们就可以编写堆排序算法了。堆排序的优点在于根节点的值始终大于所有值，因此我们可以将其放在已排序数组的末尾，然后将其从堆中移除，然后再次对二叉树进行堆化，使较大的值再次位于顶部。
示例：

来自维基百科的 Gif
代码：



    #Heap Sort Algorithm

    def createHeap(data, length, index):

        largest = index
        left = 2 * index + 1
        right = 2 * index + 2

        if left < length and data[index] < data[left]:
            largest = left

        if right < length and data[largest] < data[right]:
            largest = right

        if largest != index:
            data[index], data[largest] = data[largest], data[index]
            createHeap(data, length, largest)

    def heapSort(data):
        length = len(data)

        #We build max heap
        for index in range(length, 0, -1):
            createHeap(data, length, index)

        for index in range(length -1, 0, -1):
            data[index], data[0] = data[0], data[index]

            createHeap(data, index, 0)

        print(data)

堆排序在所有情况下（最佳情况、平均情况和最坏情况）的时间复杂度均为 O(n*log(n))，这使得它成为最常用的排序算法之一。
当你只需要知道一组元素中的“最小值”（或“最大值”），而无需担心剩余元素保持排序顺序时，堆排序非常适用。例如，优先级队列。

结论

在本文中，我展示了你必须了解的算法及其在 Python 中的实现。每篇文章都可以做得更好，所以欢迎在评论区提出你的建议或问题。

如果您也认为我遗漏了一些重要的排序算法，请告诉我。🤠

检查此repo中所有排序算法的代码。

文章来源：https://dev.to/koladev/8-must-know-sorting-algorithms-5ja