回到老问题:我最终如何编写数独求解算法
快速提示:本文将部分涉及技术,部分涉及个人故事,部分涉及文化批判。如果您只是为了代码和解释而来,请直接跳至“初始方法”标题!
这个故事始于几年前大学计算机科学课堂。我编程之路走得并不寻常——大学二年级时,我偶然选了一门计算机科学课,因为我有额外的学分,而且很好奇这门课讲的是什么。我以为我们会学习如何使用微软Word和Excel——但我当时真的不知道代码是什么。我的高中根本没有编程课,他们几乎没有能用的电脑!我既不玩电子游戏,也不参加那些传统上引导孩子们学习编程的活动。所以,当我在大学上那门Python课的时候,编程对我来说还是全新的。
我一走进教室,他们就让我们在 Idle(Python 语言自带的文本编辑器)里输入 Python 代码。他们把代码打印出来,让我们输入运行——我立刻就被迷住了。在那节课上,我编写了一个井字游戏脚本,用 GUI 输入棋子,还模仿了 Flappy Bird 的风格。说实话,这对我来说很容易,而且我玩得很开心。我很快就决定辅修计算机科学,我只是想写更多的代码。
下个学期,我选修了计算机科学系的下一门课——数据结构与算法。这门课是用C++讲授的,我当时并不知道这门课应该在开课前的暑假学习。很快我就发现,教授们想利用这门课筛选学生——很多第一天报名的学生都坚持到了下学期。我们甚至把教室从报告厅换成了休息室。我的自尊心成了我留在课堂上的唯一动力。几乎每节课我都感到完全迷失。我花了很多个通宵做项目,准备考试。
有一道题特别让我头疼——我们被要求用 C++ 写一个程序,能解决任何数独问题。我又花了无数个小时完成作业,试图让代码跑起来。到了项目截止时间,我的解决方案只通过了部分测试用例,但并非全部。最终我的作业得了 C+——这是我大学期间最差的成绩之一。
那个学期之后,我放弃了辅修计算机科学的想法,完全放弃了编码,坚持我认为我擅长的——写作和政治。
当然,生活中会发生有趣的事情,我显然又开始编码了,但我花了很长时间才感觉自己是一个称职的程序员。
话虽如此,几年后,在我的编程生涯中,我决定重新尝试实现数独解题算法,以证明我现在可以实现它。代码并不完美,但它几乎可以解决任何数独难题。让我们先来了解一下算法,然后再讨论它的实现。
数独谜题
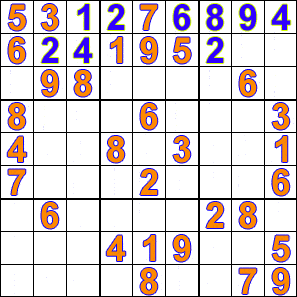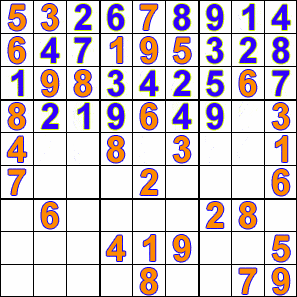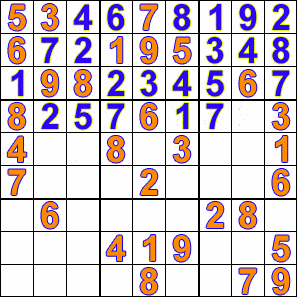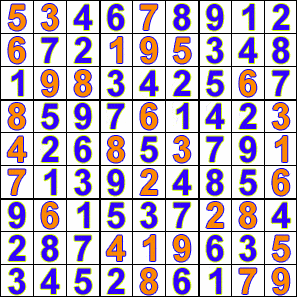
如果你以前没玩过数独,那么我来解释一下:数独是一种数字谜题,谜题中的每一行、每一列以及每个 3x3 的方格都必须恰好出现一次 1-9 的数字。有很多方法可以解决这类谜题,其中很多方法可以用计算机代替人工完成。通常,当我们用计算机解决数独问题时,我们会使用嵌套数组来表示数独棋盘,如下所示:
puzzle = [[5, 3, 0, 0, 7, 0, 0, 0, 0],
[6, 0, 0, 1, 9, 5, 0, 0, 0],
[0, 9, 8, 0, 0, 0, 0, 6, 0],
[8, 0, 0, 0, 6, 0, 0, 0, 3],
[4, 0, 0, 8, 0, 3, 0, 0, 1],
[7, 0, 0, 0, 2, 0, 0, 0, 6],
[0, 6, 0, 0, 0, 0, 2, 8, 0],
[0, 0, 0, 4, 1, 9, 0, 0, 5],
[0, 0, 0, 0, 8, 0, 0, 7, 9]]
解决后,零将被填充为实际数字:
solution = [[5, 3, 4, 6, 7, 8, 9, 1, 2],
[6, 7, 2, 1, 9, 5, 3, 4, 8],
[1, 9, 8, 3, 4, 2, 5, 6, 7],
[8, 5, 9, 7, 6, 1, 4, 2, 3],
[4, 2, 6, 8, 5, 3, 7, 9, 1],
[7, 1, 3, 9, 2, 4, 8, 5, 6],
[9, 6, 1, 5, 3, 7, 2, 8, 4],
[2, 8, 7, 4, 1, 9, 6, 3, 5],
[3, 4, 5, 2, 8, 6, 1, 7, 9]]
初步方法
因为我不想写一个包含各种谜题的完整测试套件,所以我用CodeWars上的挑战来测试自己。我尝试的第一个问题是这样的——所有谜题都是“简单”的数独题,不需要更复杂的算法就能解决。
我决定尝试用我个人习惯的方法来解决数独——我会找出某个空格里可能的数字,记录下来,如果只有一个可能的数字,就把它填到那个位置。因为这些数独比较简单,所以这种方法在这个套路里很有效,我通过了。
这是我的(未清理的)代码!
class SudokuSolver:
def __init__(self, puzzle):
self.puzzle = puzzle
self.box_size = 3
def find_possibilities(self, row_number, column_number):
possibilities = set(range(1, 10))
row = self.get_row(row_number)
column = self.get_column(column_number)
box = self.get_box(row_number, column_number)
for item in row + column + box:
if not isinstance(item, list)and item in possibilities:
possibilities.remove(item)
return possibilities
def get_row(self, row_number):
return self.puzzle[row_number]
def get_column(self, column_number):
return [row[column_number] for row in self.puzzle]
def get_box(self, row_number, column_number):
start_y = column_number // 3 * 3
start_x = row_number // 3 * 3
if start_x < 0:
start_x = 0
if start_y < 0:
start_y = 0
box = []
for i in range(start_x, self.box_size + start_x):
box.extend(self.puzzle[i][start_y:start_y+self.box_size])
return box
def find_spot(self):
unsolved = True
while unsolved:
unsolved = False
for row_number, row in enumerate(self.puzzle):
for column_number, item in enumerate(row):
if item == 0:
unsolved = True
possibilities = self.find_possibilities(
row_number, column_number)
if len(possibilities) == 1:
self.puzzle[row_number][column_number] = list(possibilities)[
0]
return self.puzzle
def sudoku(puzzle):
sudoku = SudokuSolver(puzzle)
return sudoku.find_spot()
当然,我也想解决更困难的数独难题,所以我决定实施更复杂的算法来解决这些难题。
算法
解决数独谜题的一种算法是回溯算法。本质上,你不断在空位上尝试数字,直到没有可能的数字为止,然后回溯并在之前的空位上尝试不同的数字。
向维基百科致敬,感谢它提供的出色可视化效果!
我做的第一件事是继续使用我的“简易”数独解题器的方法,根据每个方格所在行、列和方框中已有的值,找到该方格的可能值。我将所有这些值存储在一个列表中,以便在回溯或查找该方格中应该使用的值时快速引用它们。
接下来,我需要实现将物品放入每个格子中的正向移动和回溯。我在每个非给定格子(也就是游戏开始时为零的格子)上放置标记,以便这些格子包含在回溯中,而给定格子则不包含在内。然后,我遍历了那些未解的格子。我会将可能值列表中的第一个元素放入该格子,然后移至下一个未解的格子。之后,我会将该格子的第一个可能值放入该格子。如果它与前一个格子的值冲突,我会移至可能值列表中的第二个元素,然后移至下一个格子。该过程将持续进行,直到给定格子没有可能的移动方式——即到达可能值列表的末尾,并且该行、列或方框中的任何值都无效。然后,回溯算法开始生效。
在回溯实现中,代码会回到最后一个填入的位置,然后移动到下一个可能的值,再继续向前移动。如果此时也到达了最后一个可能的值,回溯算法就会继续向后移动,直到找到一个可以递增的位置。
一旦到达谜题的末尾并且每个方格中的值都正确,谜题就解决了!
我的方法
我喜欢面向对象的方法,所以我的解决方案中有两个不同的类:一个用于单元格,一个用于数独板。我的代码非常不完善,如下所示:
class Cell:
"""One individual cell on the Sudoku board"""
def __init__(self, column_number, row_number, number, game):
# Whether or not to include the cell in the backtracking
self.solved = True if number > 0 else False
self.number = number # the current value of the cell
# Which numbers the cell could potentially be
self.possibilities = set(range(1, 10)) if not self.solved else []
self.row = row_number # the index of the row the cell is in
self.column = column_number # the index of the column the cell is in
self.current_index = 0 # the index of the current possibility
self.game = game # the sudoku game the cell belongs to
if not self.solved: # runs the possibility checker
self.find_possibilities()
def check_area(self, area):
"""Checks to see if the cell's current value is a valid sudoku move"""
values = [item for item in area if item != 0]
return len(values) == len(set(values))
def set_number(self):
"""changes the number attribute and also changes the cell's value in the larger puzzle"""
if not self.solved:
self.number = self.possibilities[self.current_index]
self.game.puzzle[self.row][self.column] = self.possibilities[self.current_index]
def handle_one_possibility(self):
"""If the cell only has one possibility, set the cell to that value and mark it as solved"""
if len(self.possibilities) == 1:
self.solved = True
self.set_number()
def find_possibilities(self):
"""filter the possible values for the cell"""
for item in self.game.get_row(self.row) + self.game.get_column(self.column) + self.game.get_box(self.row, self.column):
if not isinstance(item, list) and item in self.possibilities:
self.possibilities.remove(item)
self.possibilities = list(self.possibilities)
self.handle_one_possibility()
def is_valid(self):
"""checks to see if the current number is valid in its row, column, and box"""
for unit in [self.game.get_row(self.row), self.game.get_column(self.column), self.game.get_box(self.row, self.column)]:
if not self.check_area(unit):
return False
return True
def increment_value(self):
"""move number to the next possibility while the current number is invalid and there are possibilities left"""
while not self.is_valid() and self.current_index < len(self.possibilities) - 1:
self.current_index += 1
self.set_number()
class SudokuSolver:
"""contains logic for solving a sudoku puzzle -- even very difficult ones using a backtracking algorithm"""
def __init__(self, puzzle):
self.puzzle = puzzle # the 2d list of spots on the board
self.solve_puzzle = [] # 1d list of the Cell objects
# the size of the boxes within the puzzle -- 3 for a typical puzzle
self.box_size = int(len(self.puzzle) ** .5)
self.backtrack_coord = 0 # what index the backtracking is currently at
def get_row(self, row_number):
"""Get the full row from the puzzle based on the row index"""
return self.puzzle[row_number]
def get_column(self, column_number):
"""Get the full column"""
return [row[column_number] for row in self.puzzle]
def find_box_start(self, coordinate):
"""Get the start coordinate for the small sudoku box"""
return coordinate // self.box_size * self.box_size
def get_box_coordinates(self, row_number, column_number):
"""Get the numbers of the small sudoku box"""
return self.find_box_start(column_number), self.find_box_start(row_number)
def get_box(self, row_number, column_number):
"""Get the small sudoku box for an x and y coordinate"""
start_y, start_x = self.get_box_coordinates(row_number, column_number)
box = []
for i in range(start_x, self.box_size + start_x):
box.extend(self.puzzle[i][start_y:start_y+self.box_size])
return box
def initialize_board(self):
"""create the Cells for each item in the puzzle and get its possibilities"""
for row_number, row in enumerate(self.puzzle):
for column_number, item in enumerate(row):
self.solve_puzzle.append(
Cell(column_number, row_number, item, self))
def move_forward(self):
"""Move forwards to the next cell"""
while self.backtrack_coord < len(self.solve_puzzle) - 1 and self.solve_puzzle[self.backtrack_coord].solved:
self.backtrack_coord += 1
def backtrack(self):
"""Move forwards to the next cell"""
self.backtrack_coord -= 1
while self.solve_puzzle[self.backtrack_coord].solved:
self.backtrack_coord -= 1
def set_cell(self):
"""Set the current cell to work on"""
cell = self.solve_puzzle[self.backtrack_coord]
cell.set_number()
return cell
def reset_cell(self, cell):
"""set a cell back to zero"""
cell.current_index = 0
cell.number = 0
self.puzzle[cell.row][cell.column] = 0
def decrement_cell(self, cell):
"""runs the backtracking algorithm"""
while cell.current_index == len(cell.possibilities) - 1:
self.reset_cell(cell)
self.backtrack()
cell = self.solve_puzzle[self.backtrack_coord]
cell.current_index += 1
def change_cells(self, cell):
"""move forwards or backwards based on the validity of a cell"""
if cell.is_valid():
self.backtrack_coord += 1
else:
self.decrement_cell(cell)
def solve(self):
"""run the other functions necessary for solving the sudoku puzzle"""
self.move_forward()
cell = self.set_cell()
cell.increment_value()
self.change_cells(cell)
def run_solve(self):
"""runs the solver until we are at the end of the puzzle"""
while self.backtrack_coord <= len(self.solve_puzzle) - 1:
self.solve()
def solve(puzzle):
solver = SudokuSolver(puzzle)
solver.initialize_board()
solver.run_solve()
return solver.puzzle
我的收获
有时候,这真的需要时间和练习——我大学时花了无数时间研究的数独解题器,几年后只用了不到一个小时就搞定了。我想说的是,计算机科学课程的起步阶段往往不允许那些早年没有写过代码的人参与,几年后随着计算机科学教育政策的改变,这种情况或许可以接受,但目前,这排除了那些在小镇长大、从小对编程不感兴趣或高中教育背景较差的人。在某种程度上,这无疑促成了编程训练营的成功,它们从基础开始,教授那些概念性较低的网页开发技能,而不是繁琐的算法。
我现在可以编写数独解题算法,但我并不认为这是开发人员必备的技能——在我无法实现数独解题器的那段时间之后不久,我仍然是一位成功的软件工程师。我确实认为一些计算机科学基础知识非常有帮助,即使对于新手开发人员也是如此。例如,大O符号背后的概念对于选择不同的方法非常有帮助。话虽如此,大多数数据结构和算法并非日常使用,那么为什么它们会成为面试和计算机科学课程的基础,而不是那些每天都会用到的更重要的东西呢?
我很高兴看到自己在编码方面的个人成长;然而,我迫不及待地希望有一天开发人员不再需要克服想象中的困难来证明自己,学习环境也变得更加建设性。
文章来源:https://dev.to/aspittel/how-i-finally-wrote-a-sudoku-solver-177g 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com