再打我一次宝贝 - 什么是缓存命中以及你为什么要关心它?
动机
矩阵乘法示例
计算机体系结构
矩阵乘法再探
最后的想法
动机
在推导算法性能时,我们经常会考虑复杂度。尤其是在比较不同算法时,考察渐近复杂度(例如大 O 符号)非常有用。然而,我们必须记住,大 O 符号会“吞噬”除最大复杂度因素之外的所有因素。一个突出的例子是,在集合中查找值时,大 O 符号可能会产生误导。哈希映射是这种用例的默认候选者,因为访问某个特定元素需要常数时间。但是,如果元素很少,使用树或甚至简单的列表可能会更快。
虽然你应该留意类似情况,但还有另一个影响性能的重要因素:计算机硬件/架构。你的 CPU 可能很快,但它必须等待 I/O 完成。你的分布式算法可能很强大,但你的网络拓扑却不够用。在这篇博文中,我们将探讨计算机架构中一个可能对算法性能产生数量级影响的特定部分:内存层次结构——尤其是CPU 缓存。
这篇文章的结构如下。首先,我们将看一个非常常见的示例,其中运行时性能很大程度上受 CPU 缓存利用率的影响。第二部分将介绍一些计算机体系结构的理论背景,帮助读者理解示例中的具体内容。之后,我们将运用新学到的知识重新回顾第一部分中的示例。最后,我们将总结主要思想来结束这篇博文。
矩阵乘法示例
公式
我们要用一个非常基础的例子:矩阵乘法。矩阵乘法在很多领域都有应用,例如图像处理、人工智能、机器人技术、数据压缩。对于矩阵A * B = C的乘法,公式如下:
对于结果矩阵的每个元素,它按行遍历A,按列遍历B,将每对元素相乘,然后将结果相加。该公式还有一个很好的可视化表示:
现在让我们看一下该算法的两种不同变体,并测量不同矩阵大小的执行时间。为了简单起见,我们使用两个方阵。它们填充了随机生成的双精度值。
我们使用ScalaMeter来测量运行时性能。欢迎查看我上一篇博文,其中详细介绍了该工具。
实验
算法1
第一个算法是上述公式的简单实现。对于两个大小为n的方阵,它必须执行n³ 次乘法和加法,因此复杂度为O(n³)。
def mult1(m1: Array[Array[Double]],
m2: Array[Array[Double]],
size: Int): Array[Array[Double]] = {
var res = Array.fill(size)(new Array[Double](size))
var i = 0
while (i < size) {
var j = 0
while (j < size) {
var k = 0
while (k < size) {
res(i)(j) += m1(i)(k) * m2(k)(j)
k += 1
}
j += 1
}
i += 1
}
res
}
算法2
第二种算法在应用公式的细微变化之前,对第二个矩阵进行转置,使乘法运算中第二个矩阵的索引取反。对于两个大小为n的方阵,它首先必须执行n² 次复制操作,然后再执行n³次乘法和加法。这也导致了O(n³)复杂度,但开销更大。
def mult2(m1: Array[Array[Double]],
m2: Array[Array[Double]],
size: Int): Array[Array[Double]] = {
var m2t = Array.fill(size)(new Array[Double](size))
var x = 0
while (x < size) {
var y = 0
while (y < size) {
m2t(x)(y) = m2(y)(x)
y += 1
}
x += 1
}
var res = Array.fill(size)(new Array[Double](size))
var i = 0
while (i < size) {
var j = 0
while (j < size) {
var k = 0
while (k < size) {
res(i)(j) += m1(i)(k) * m2t(j)(k)
k += 1
}
j += 1
}
i += 1
}
res
}
结果
综合考虑这两种算法,一个合理的猜测是,第一种算法比第二种算法更快,因为除了转置运算和倒排索引之外,它们几乎完全相同。两者之间的相对差异应该会随着规模的增加而减小,因为n³ 的增长速度比n²更快,这也反映在两种算法具有相同的渐近复杂度上。然而,由于需要先转置矩阵,因此对内存的要求mult2略高一些。
让我们看看对于不同矩阵大小n的两种实现的执行时间。我们还添加了一列,表示选择第二种实现时获得的加速比 ( mult1/ - 1 )。mult2
| n | 时间mult1(毫秒) |
时间mult2(毫秒) |
加速 |
|---|---|---|---|
| 10 | 0.011 | 0.014 | -20.5% |
| 50 | 0.166 | 0.128 | 29.6% |
| 100 | 1.307 | 1.102 | 18.5% |
| 500 | 242.1 | 147.4 | 64.2% |
| 1000 | 9 347 | 1 244 | 651.2% |
| 3000 | 398 619 | 33,846 | 1077.7% |
令人印象深刻!即使我们做了额外的工作,mult2当n = 3000 时,速度也提高了 10 倍以上!发生了什么?
在开始解释之前,了解一些计算机架构的基础知识会很有帮助。下一节将涵盖这部分内容。如果您已经熟悉这些内容,或者迫不及待地想知道答案,请跳过下一节,稍后再阅读。
计算机体系结构
冯·诺依曼架构
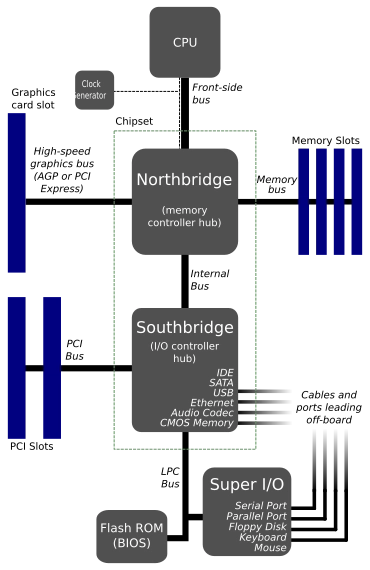
大多数现代计算机,尤其是商用计算机,都基于冯·诺依曼体系结构。该体系结构最初于 1945 年提出,并随着时间的推移逐渐演变为今天的样子。它描述了计算机的基本组件,例如 CPU、内存和 I/O 设备,以及它们如何协同工作。
下图描述了主要组件及其连接方式。中央处理器 (CPU) 负责执行计算工作,例如算术运算。它通过北桥连接到主随机存取存储器 (RAM)。北桥还连接其他高速接口,但我们在此不再赘述。如果数据不在内存中,则必须从持久性存储器加载。用于此目的的各种接口(例如 IDE、SATA、USB)通过南桥连接。
这意味着处理器与数据之间没有直接连接。如果数据在主存中,则必须经过北桥;如果数据不在主存中,则也必须经过南桥。这种存储层次结构是必要的,因为需要在存储成本、速度和大小之间进行权衡。
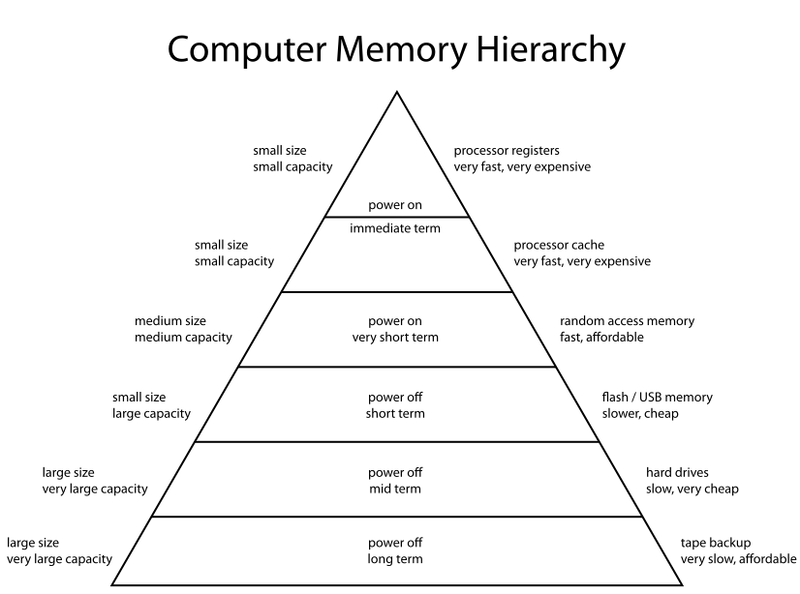
存储层次结构
存储可分为持久性存储和易失性存储。为了确保数据在计算机重启后仍然有效,需要将其持久存储,例如存储在硬盘驱动器 (HDD) 或固态硬盘 (SSD) 中。这类存储的缺点是通常未针对随机访问进行优化(这对于文件来说没问题,但对于单个数据或代码可能并非如此)。此外,它距离 CPU 非常远,这会增加额外的传输延迟。
启动操作系统时,所有必需的数据都会加载到易失性主存储器中。如果计算机断电,数据将会丢失。此外,主存储器通常要小得多。然而,它的速度更快,尤其是在延迟方面,并且针对随机访问进行了优化。
虽然将 RAM 用于更常用的数据是个好主意,但这仍然不是最佳选择,因为 CPU 需要通过北桥来读取或修改数据。为了解决这个问题,计算机中增加了另一层内存:CPU 缓存。
商用主存储器通常基于动态随机存取存储器 ( DRAM )。DRAM 的每个元件基本上只包含一个晶体管和一个电容器,价格低廉且易于封装,从而提供更大的容量。然而,由于其设计原因,它的速度比静态随机存取存储器 ( SRAM ) 慢得多,而 SRAM 通常用于需要更低延迟的情况。SRAM 用于 CPU 缓存。下图总结了我们之前讨论的存储层次结构。
CPU 缓存本身通常也分为不同的层级,从速度最快但缓存容量最小的一级缓存 (L1) 到速度最慢但缓存容量最大的三级缓存 (L3)。此外,L1 缓存还分为数据缓存 (L1d) 和指令/代码缓存 (L1i)。
如果您使用的是多核 CPU,则部分缓存会在各个核心之间共享。如果启用了超线程,实际的缓存大小很大程度上取决于您正在执行的程序,因为两个超线程必须共享同一个缓存。想要了解更多关于此主题的详细信息,我建议您阅读 Ulrich Drepper 撰写的精彩论文《每个程序员都应该知道的内存知识》。
为了让读者了解不同层的实际大小,下表包含我 2016 年笔记本电脑的规格。
| 贮存 | 尺寸 |
|---|---|
| L1i缓存 | 32 KB |
| L1d缓存 | 32 KB |
| 二级缓存 | 256 KB |
| L3缓存 | 4 MB |
| 主存储器 | 16 GB |
| 固态硬盘 | 500 GB |
CPU 缓存使用率
缓存存储了常用主内存位置的数据副本。虽然将数据存储在磁盘还是内存中是程序员的慎重决定,但缓存中存储的内容大多是在后台管理的。
数据以固定大小的块(即所谓的缓存行 )在主存和缓存之间传输。缓存条目包含数据以及它所缓存的内存位置。每当 CPU 需要访问某个内存位置时,它首先会在缓存中查找相应的条目。如果该条目存在,则称为缓存命中,否则称为缓存未命中。
缓存命中通常是理想的,因为它可以避免(相对)昂贵的主内存访问。需要注意的是,缓存未命中是无法避免的,而且通常情况下并非坏事。如果某个内存位置是第一次访问,那么缓存未命中是正常的。
然而,现代 CPU 也具备避免这种情况发生缓存未命中的机制。处理器有一个负责预取缓存行的小模块。例如,当处理结构类型(例如一个人)并访问该人的一个属性(例如地址)时,很可能稍后会访问另一个属性。因此,CPU 还会预取其他属性,例如年龄和姓名。另一个例子是数组的顺序访问。当访问数组的第一个元素时,CPU 会在处理第一个元素的同时并行预取更多元素。
了解了这些知识后,我们想回到矩阵乘法的原始示例,并分析为什么mult2对于更大的矩阵,其表现比 好得多mult1。
矩阵乘法再探
在最初的例子中,我们有两种矩阵乘法的实现:mult1和mult2。两者本质上是相同的,只是mult2在进入执行计算的三个嵌套循环之前对第二个矩阵进行了转置。但为什么这会产生差异呢?为什么这种差异只在更大的矩阵中才显现出来?
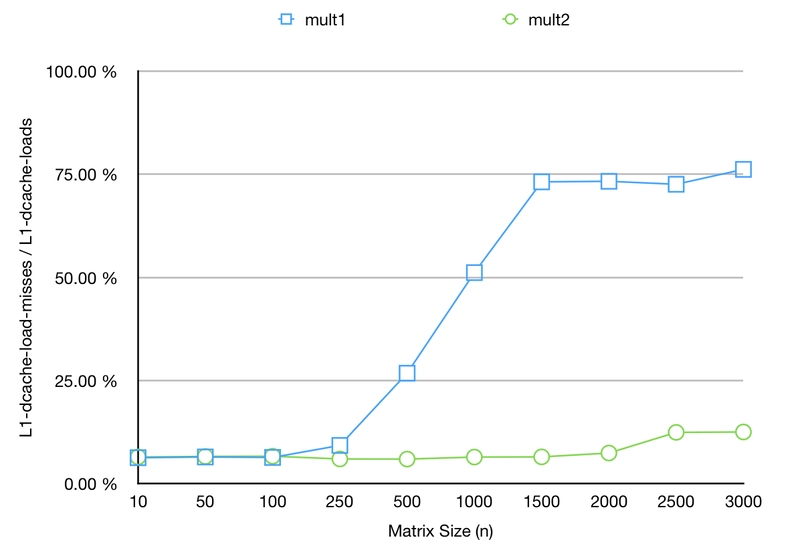
在从更理论的角度分析差异之前,我们先来看一些数据。我们将使用不同的矩阵大小再次执行这两种实现。不过,这次我们不测量运行时间,而是使用 来查看 L1d 缓存未命中的 CPU 计数器perf。
for s in 10 50 100 250 500 1000 1500 2000 2500 3000
do
for m in 1 2
do
# Run mult$m with size $s and record CPU counters
perf stat -e L1-dcache-loads,L1-dcache-load-misses \
java -jar cpumemory.jar $s $m
done
done
可以看到,从n >= 250开始,L1d 缓存未命中率会随着 而增加mult1。这意味着 CPU 必须回退到更大但更慢的 L2 缓存。这会浪费一些周期,等待更高级别的内存提供所需数据。但为什么会这样呢?
如上一节所述,CPU 正在将数据预取到缓存中。这意味着,当访问矩阵的第一个元素时,它将并行预取更多元素。回顾一下包含三个索引i、j和 的三个嵌套循环k。
首次访问m1(i)(k)将触发预取更多元素,例如。然而,m1(i)(k + 1)首次访问将触发预取。虽然只要整个矩阵能放入缓存,这不是什么大问题,但更大的矩阵就变成了一个整体。m2(k)(j)mult1m2(k)(j + 1)
最内层循环递增的是k,而不是。因此,当增加j时,可能已经被驱逐了。这就是为什么它在更大的矩阵中表现更好的原因。通过转置矩阵,然后交换对 的访问,即使缓存已满,矩阵的某些部分必须被驱逐,我们至少可以为内层循环正确地预取。jm2(k)(j + 1)mult2m2t(j)(k)
最后的想法
在这篇博文中,我试图解释为什么作为一名软件开发人员,了解一些计算机架构的基础知识至关重要。虽然大多数大学计算机科学家在学习期间都应该学习这些知识,但对于其他编写代码的人来说,多了解一些这方面的知识无疑是一个好主意。
我们研究了一种朴素矩阵乘法算法的实现,只需更改一些小细节,执行速度就能提升 1000% 以上。需要注意的是,这mult2远非最优实现。您可以参阅论文《基于皮亚诺曲线的元素排序实现缓存无关矩阵乘法》,其中提供了一种缓存优化的实现,它不依赖于实际缓存大小。另请注意,还有其他算法的渐近复杂度优于O(n³),例如Strassen 算法。
您是否遇到过由于缓存未命中而导致程序运行缓慢的情况?您perf以前遇到过这种情况吗?您是否认为开发人员应该更加了解缓存逻辑才能编写出高效的程序?请在评论区留言,分享您的想法!
如果您喜欢这篇文章,您可以在 ko-fi 上支持我。
文章来源:https://dev.to/frosnerd/hit-me-baby-one-more-time---what-are-cache-hits-and-why-should-you-care-4500 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com