彻底学习大 O 符号

2025-05-24

彻底学习大 O 符号

介绍

最近，我在一家非常酷的公司参加一个我非常想要的职位的面试，其中一个步骤就是可怕的代码面试，我们会现场解决 LeetCode 问题。

我得到了解决方案，当被问及解决方案的大 O 函数时，我回答正确，但我很困惑，可能只是通过简单地计算循环就偶然发现了它。

为了将来不再在求职面试中失败，我在大学第一次了解这个话题几年后再次回顾这个话题。

这篇文章的主要目的是为我在编程面试前提供一份快速总结和复习资料。虽然我通过写作来学习，但把这些资料保存在某个地方，以便需要时随时查阅也很重要。嘿，也许它也适合你。

非常感谢NeetCode提供如此多的资料并免费教授所有这些内容。

什么是 Big O 时间复杂度？

在计算机科学中，大 O 符号用于根据算法的运行时间或空间需求如何随着输入大小的增长而增长来对算法进行分类。[...] [它]根据函数的增长率来表征函数：具有相同渐近增长率的不同函数可以使用相同的 O 符号表示。

  • 来源：维基百科

或者换句话说，这是一种分析算法在输入增加时运行时间的方法。O表示整个操作，n表示输入。

让我们看一些例子，它会更有意义。

O（n）-当然，给我一个例子

也许最容易理解的例子是 O(n)，其中增长率是线性的。

  • 给定一个未排序的数组n，编写一个返回最大值的函数。

为了解决这个问题，我们需要遍历数组n中的每个项目，并在找到比前一个更大的值时将其存储。

n = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5] # Initialize the array of n
def find_max_value(arr):
    # Initialize the maximum value with the first element of the array
    max_value = arr[0]

    # Iterate through the array to find the maximum value
    for num in arr:
        if num > max_value:
            max_value = num

    return max_value
print(find_max_value(n)) # Output: 9
Enter fullscreen mode Exit fullscreen mode

前面的算法总是会至少运行一次n中的每个项目 - 它必须这样做，因为数组是未排序的。

因此，我们说该算法的时间复杂度为O(n)，因为随着数组大小（n）的增长，运行时间以线性方式增长。

它也不关心算法的非常量属性。假设你的算法恰好迭代n中的每个项两次，导致时间复杂度为O(2n)。我们将其简化为 O(n)，因为大 O 符号的首要任务是表达运行时间的增长形状。

O(1) - 第一个也是唯一一个例外

在告诉你我们不必关心符号中的非常量值之后，我们必须讨论O(1)，其中n甚至在这个分类中不存在。这也许是最理想的速率，其中时间不会随着输入的增长而增长，保持恒定。例如：

  • 给定一个非空数组，返回第一个元素。
n = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5] # Initialize the array of n
def first_element(arr):
    # Return the first element of the array
    return arr[0]
print(first_element(n)) # Output: 3
Enter fullscreen mode Exit fullscreen mode

因为我们实际上并没有遍历数组中的任何项目，所以此操作的符号为O(1)。

其他一些示例包括将项目附加到数组、删除（pop），或者在使用哈希映射（或字典）时，我们只需使用索引进行查找 - 就像上面的算法一样。

O（n^2）-这似乎很容易

这种符号最简单的情况是当您有嵌套循环或二维数组时，您必须遍历它们才能找到您要查找的内容。

  • 给定一个骰子的面数，计算使用两个给定大小的骰子时的所有可能组合
def dice_combinations(sides):
    # Initialize combinations array
    combinations = []
    # Iterate through first side
    for i in range(1, sides + 1):
        # Add every combination possible
        for j in range(1, sides + 1):
            combinations.append((i, j))
    return combinations

sides = 6  # Example for a 6-sided dice
print(dice_combinations(sides))
# Output: An array with 36 items (6 * 6)
# [(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)]
Enter fullscreen mode Exit fullscreen mode

但如果骰子的面不同怎么办？

O(n*m) - 好的，现在你只需添加字母

相反，如果您必须使用两个不同面的骰子来计算可能的组合，则它们的工作原理如下。

  • 给定一个骰子的两个面数，计算掷这两个骰子时所有可能的组合。
def two_dice_combinations(sides1, sides2):
    # Initialize combinations array
    combinations = []
    # Iterate through first side
    for i in range(1, sides1 + 1):
        # Add every combination possible
        for j in range(1, sides2 + 1):
            combinations.append((i, j))
    return combinations

sides1 = 6  # Example for a 6-sided dice
sides2 = 8  # Example for an 8-sided dice
print(two_dice_combinations(sides1, sides2))
# Output: An array with 48 items (6 * 8)
# [(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (5, 7), (5, 8), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6), (6, 7), (6, 8)]
Enter fullscreen mode Exit fullscreen mode

请记住，这些算法可以无限期地工作。如果我们有三个骰子，你可以得到一个O(n^3) 的算法，甚至O(n^5) 的算法——数学上没有限制。

O（log n）——什么？

大多数人甚至不明白log的含义，而只是记住在进行某种二分查找时会使用这种符号。

这种情况是，对于循环的每次迭代，我们将循环减半用于下一次迭代。log n部分就变成了我们可以将 n 除以 2 多少次才能得到结果——这有点像底数为 2 时对数符号的定义。

使用二叉树时，我们必须遍历节点，并且在每个节点上做出决定——向“左”走还是向“右”走。由于我们只朝一个方向走，这已经将操作量减半了（不必介意节点的子节点数量可能不同）。

这是最好的算法之一，因为运行时间增长非常缓慢。对于非常大的输入，时间增长基本上是一条直线。

O(log n) 最常见的例子是我们进行二分搜索时。

我不会讲太多细节，但基本上当我们有一个排序数组并想要找到特定值的索引时，可以使用二进制搜索。

  • 给定一个排序数组，找到目标值的索引
def binary_search(arr, target):
    # Initialize the left and right pointers as the first and last
    left, right = 0, len(arr) - 1

    # Continue searching while the left pointer is less than or equal to the right pointer
    while left <= right:
        # Calculate the middle index
        mid = (left + right) // 2

        # Check if the middle element is the target
        if arr[mid] == target:
            return mid
        # If the middle element is less than the target, adjust the left pointer
        elif arr[mid] < target:
            left = mid + 1
        # If the middle element is greater than the target, adjust the right pointer
        else:
            right = mid - 1

    # Return -1 if the target is not found in the array
    return -1

# Example usage:
sorted_array = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
target = 7
print(binary_search(sorted_array, target)) # Output: 6 - sorted_array[6] == 7
Enter fullscreen mode Exit fullscreen mode

请注意，循环并不在我们所熟悉的中，而是在和索引for i in range(1, n)之间的中间。leftright

O(n log n) - 现在你只是在编造东西

之所以在这里这样做，是因为很难直观地弄清楚这一点。

这种符号通常出现在排序算法中，事实上它是现代语言中内置排序函数中最常见的符号。

以归并排序为例。为了避免过多细节，我们简单介绍一下，它的基本原理是将数组递归地分成两半（log n 次划分），然后在线性时间内将两半合并在一起（每次合并的时间复杂度为 O(n)。将这两个步骤结合起来，我们得到了O(n * log n)。

  • 给定一个未排序的数组，使用合并排序对其进行排序。
def merge_sort(arr):
    if len(arr) <= 1:
        return arr

    # Find the middle point and divide the array into two halves
    mid = len(arr) // 2
    left_half = arr[:mid]
    right_half = arr[mid:]

    # Recursively sort the two halves
    left_sorted = merge_sort(left_half)
    right_sorted = merge_sort(right_half)

    # Merge the sorted halves
    return merge(left_sorted, right_sorted)

def merge(left, right):
    sorted_array = []
    left_index, right_index = 0, 0

    # Merge the two arrays while maintaining order
    while left_index < len(left) and right_index < len(right):
        if left[left_index] < right[right_index]:
            sorted_array.append(left[left_index])
            left_index += 1
        else:
            sorted_array.append(right[right_index])
            right_index += 1

    # Append any remaining elements from the left or right array
    sorted_array.extend(left[left_index:])
    sorted_array.extend(right[right_index:])

    return sorted_array

# Example usage:
unsorted_array = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]
print(merge_sort(unsorted_array)) # Output: [1, 1, 2, 3, 3, 4, 5, 5, 5, 6, 9]
Enter fullscreen mode Exit fullscreen mode

我们可以在上面的代码中看到，每次merge_sort调用 时，它都以调用 结束merge。并且每次调用 merge_sort 时，它也会调用自身两次，分别针对数组的每一半。

O（2^n）——我应该预见到的

当我们有一个以两种方式分支的递归算法时，通常会发现这种符号。

我们很容易就能看出冒泡排序的复杂性，但既然谈论算法就离不开斐波那契数列，那我们就最终解决这个问题吧。不过请记住，还有更有效的方法来解决这个问题。

  • 给定一个索引，找出斐波那契数列中的数字。
def fibonacci(n):
    if n <= 1:
        return n
    branch1 = fibonacci(n-1)
    branch2 = fibonacci(n-2)
    return branch1 + branch2

# Example usage:
print(fibonacci(5))  # Output: 5
Enter fullscreen mode Exit fullscreen mode

从上面的实现中可以清楚地看出，递归循环的每次迭代都会创建两个分支。

例如，对于n = 5，我们将调用fibonacci(4)和，这将再次fibonacci(3)生成（我们没有在上述算​​法中实现记忆化）两次和。您可以将其可视化为“倒置二叉树”，其中树的高度为n。fibonacci(3) fibonacci(2) fibonacci(1)

理论上，我们可以将任意数字提升到n次方，例如O(3^n)和O(5^n)。

O（n！）——请让它结束！

如果您不知道！的意思，我们只需将该数字乘以每个数字 -1，直到得到 1（我们可以忽略它）。

例如：
5！=5*4*3*2=120

你可以把它想象成一个算法，每次迭代都会删除一个元素并重新运行。它主要出现在排列问题中，或者更著名的旅行商问题中。

对于这个，我不会添加任何代码，因为这会变得非常复杂，而且这种情况极其罕见，因为如果你有一个O（n！）算法，那么你肯定没有最佳解决方案。

就是这样！

您可以参考下图来比较这些算法。纵轴表示操作次数（或时间），横轴表示元素数量（或n的值）。特别感谢 Eric Rowell 提供的速查表！

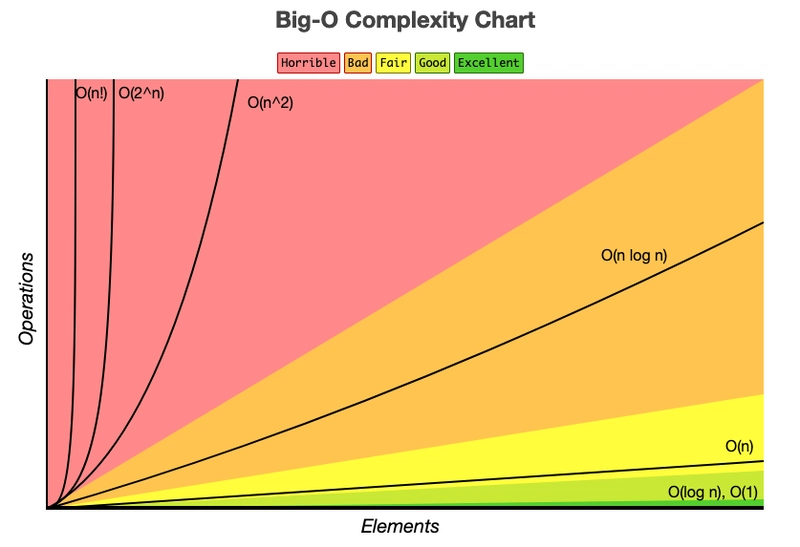
Big-O 复杂度图表
可在https://www.bigocheatsheet.com/上找到

希望这篇文章对你有帮助，祝你未来学业顺利！🤞

编辑：O（sqrt n）

写完这篇文章后，我遇到了一道 LeetCode 题目，它的解法复杂度为 O(sqrt n)。如果你感兴趣的话，可以看看另一篇博文：N 的第 K 个因数 - 一个 O(sqrt n) 算法

文章来源：https://dev.to/alvbarros/learn-big-o-notation-once-and-for-all-hm9
Devto 翻译
PREV
测试 101：测试简介
NEXT
comiCSS 简介