用 Rust 构建神经网络（从头开始）

2025-06-08

用 Rust 构建神经网络（从头开始）

让我们从零开始构建一个神经网络，以真正理解它们的工作原理。我所说的“从零开始”，是指不使用任何复杂的机器学习或线性代数库。我们将构建一个单层感知器，这是最简单的神经网络，然后教它对两个数字进行加法运算。

我将使用 Rust 语言，但如果您愿意，也可以使用 JavaScript 或 Python 实现。代码可在此处获取。

神经网络

神经网络顾名思义，就是一个人工神经元组成的网络。神经元或“节点”是模拟生物神经元功能的计算单元。它接收输入，进行数学运算，然后输出结果。

我们首先定义一个NeuralNetwork结构体，并关联一个方法来初始化它。目前我们还没有太多内容，所以暂时先留空。



struct NeuralNetwork {}

impl NeuralNetwork {
    fn new() -> Self {
        Self {}
    }
}
Enter fullscreen mode Exit fullscreen mode

图层

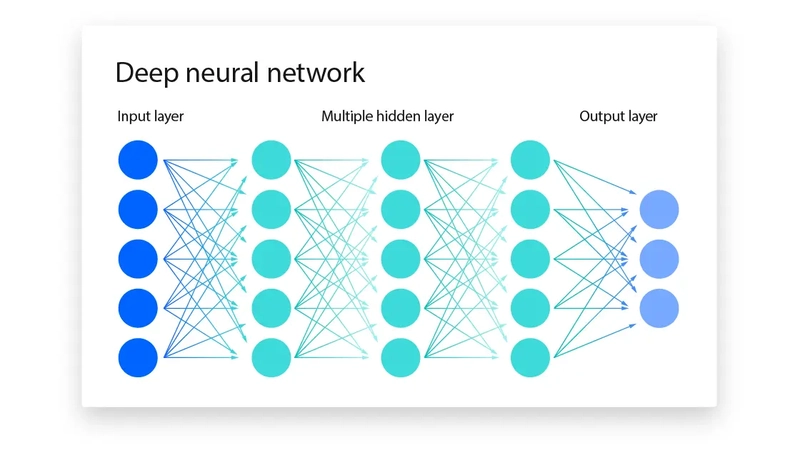
神经网络中的神经元被划分为不同的层级，称为层。每一层都以某种方式处理输入，每一层的输出作为下一层的输入。第一层接收初始输入，最后一层产生最终输出。中间的层称为隐藏层，用于从数据中提取和转换特征。

深度神经网络

每个圆圈代表一个神经元，每条线代表一个连接。你可以看到，每一层中的每个神经元都与下一层中的每个神经元相连。

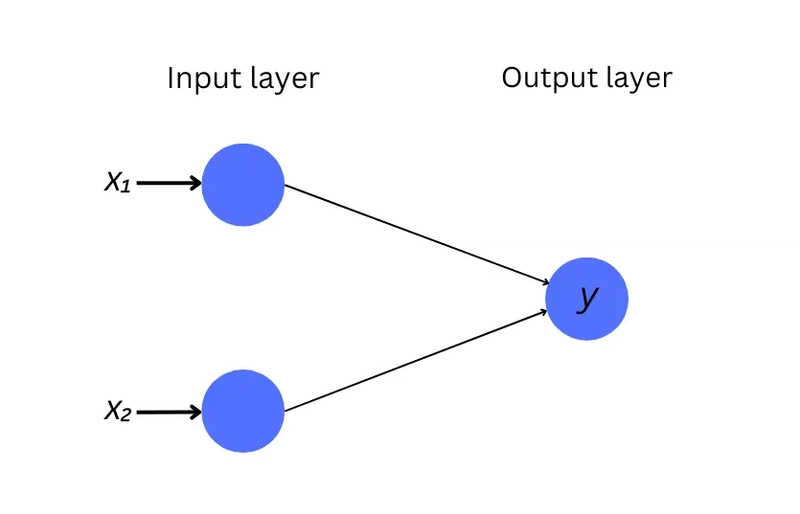
单层感知器

我们正在构建的神经网络如下所示。它有两个输入神经元（每个数字一个）和一个输出神经元。注意，它没有任何隐藏层。

权重

神经网络中的每个连接都有一个关联的权重。这些权重决定了神经元之间关系的强度和方向（正向或负向影响），进而影响数据在从一层传递到下一层时如何转换。在训练过程中，我们会调整这些权重值以减少输出中的误差。

思考权重的一个好方法是将神经连接想象成将信号（数据）从一个神经元传输到另一个神经元的管道。这些管道的粗细可以改变。管道越粗，意味着它所代表的连接越强，对通过它的信号的影响就越大。

由于我们的网络中没有隐藏层，我们只需要两个权重（每个连接一个）。我们暂时将它们初始化为随机浮点值。



struct NeuralNetwork {
    weights: Vec<f64>
}

impl NeuralNetwork {
    fn new() -> Self {
        let mut rng = rand::thread_rng();
        let weights = vec![rng.gen_range(0.0..1.0), rng.gen_range(0.0..1.0)];

        Self {
            weights
        }
    }
}
Enter fullscreen mode Exit fullscreen mode

偏见

偏差是另一个调整神经元输出的参数。想象一下，每个神经元旁边都有一个小旋钮。无论神经元接收到什么信号，这个旋钮都可以调节神经元的活跃程度。这就像调整神经元的基线活动水平，确保即使所有输入信号都很弱，神经元仍然可以根据这个偏差调整来选择触发（激活）。

只有隐藏层和输出层的神经元才有偏差。由于我们的感知器没有隐藏层，并且输出层只有一个神经元，所以我们只需要一个偏差值，并将其初始化为一个随机值。



struct NeuralNetwork {
    // [...]
    bias: f64
}

impl NeuralNetwork {
    fn new() -> Self {
        // [...]

        Self {
            // [...]
            bias: rng.gen_range(0.0..1.0)
        }
    }
}
Enter fullscreen mode Exit fullscreen mode

激活函数

激活函数决定神经元是否应该激活。它就像一个过滤器或守门人，接收输入信号（经过权重和偏差的修改后），并决定神经元的激活亮度。激活函数用于在网络中引入非线性。这种非线性使网络能够学习复杂的模式。

神经元的输出可以计算如下：

哦 你 吨 页 你 吨 = 一个 c 吨 我 五 一个 吨 我 哦 n ( 西 e 我 克 h 吨 秒 ⋅ 我 n 页 你 吨 秒 + B 我 一个 秒 ) 输出 = 激活（权重⋅输入+偏差）

我们将传出连接的权重乘以输入，加上偏差，并对结果应用激活函数。



impl NeuralNetwork {
    // [...]

    fn predict(&self, input: &[f64; 2]) -> f64 {
        let mut sum = self.bias;
        for (i, weight) in self.weights.iter().enumerate() {
            sum += input[i] * weight;
        }

        sigmoid(sum)
    }
}
Enter fullscreen mode Exit fullscreen mode

Sigmoid 是一个相对简单的非线性激活函数。它的作用是将参数转换为 0 到 1 之间的值，但转换过程并非线性的。尝试用不同的值调用它，看看它是如何工作的。



fn sigmoid(x: f64) -> f64 {
    1.0 / (1.0 + (-x).exp())
}
Enter fullscreen mode Exit fullscreen mode

反向传播

这是训练神经网络的关键算法。如果最终输出不符合预期，我们会将误差“反向”传播到网络的各个层，找出哪些路径（连接）对最终输出的整体误差贡献了多少。然后，我们会利用这些信息微调网络中的权重和偏差，以减少未来输出的误差。我们不断重复这个过程，逐渐优化网络参数，直到其输出足够接近我们的预期。



impl NeuralNetwork {

// [...]

    fn train(&mut self, inputs: Vec<[f64; 2]>, outputs: Vec<f64>, epochs: usize) {
        for _ in 0..epochs {
            for (i, input) in inputs.iter().enumerate() {

                // Get a prediction for a given input
                let output = self.predict(input);

                // Compute the difference between the actual and the desired output
                let error = outputs[i] - output;

                // Find the gradient of the loss function
                // (sort of like a hint about the direction to adjust the weights in)
                let delta = derivative(output);

                // Adjust the weights and the bias to reduce error in the output
                for j in 0..self.weights.len() {
                    self.weights[j] += self.learning_rate * error * input[j] * delta;
                }

                self.bias += self.learning_rate * error * delta;
            }
        }
    }
}

fn derivative(x: f64) -> f64 {
    x * (1.0 - x)
}
Enter fullscreen mode Exit fullscreen mode

一个epoch指的是对整个训练数据集进行一次完整的遍历。在每个 epoch 中，我们将训练数据中的每组输入输入到我们的网络中，将其输出与预期结果进行比较，并利用差异重新调整其参数。我们会重复此过程多个 epoch，以优化模型的性能。

最后一步是将学习率添加到我们的网络。它是一个常数值，决定了模型从错误中学习的速度。我们将其设置为0.1。



struct NeuralNetwork {
    // [...]
    learning_rate: f64,
}

impl NeuralNetwork {
    fn new() -> Self {
        // [...]

    Self {
        // [...]
        learning_rate: 0.1,
    }
}
Enter fullscreen mode Exit fullscreen mode

现在我们的神经网络已经准备好了，让我们使用它。



fn main() {
    let d = data::get_data().unwrap();

    let inputs = d.training_inputs;
    let outputs = d.training_outputs;
    let test_inputs = d.test_inputs;

    // Initialize the network
    let mut neural_net = NeuralNetwork::new();

    for input in test_inputs.iter() {
        // Pass a set of inputs (two numbers) and get a prediction back which should be a sum of the two numbers
        let prediction = neural_net.predict(input);
        println!("Input: {:?}, Prediction: {:.1}", input, prediction);
    }
}
Enter fullscreen mode Exit fullscreen mode

如果你运行它，你会得到一些像这样的输出。



Input: [0.9, 0.1], Prediction: 0.7
Input: [0.5, 0.5], Prediction: 0.7
Input: [0.2, 0.3], Prediction: 0.7
Input: [0.3, 0.6], Prediction: 0.7
Input: [0.1, 0.7], Prediction: 0.7
Input: [0.3, 0.1], Prediction: 0.7
Input: [0.1, 0.5], Prediction: 0.7
Input: [0.9, 0.0], Prediction: 0.7
Input: [0.3, 0.3], Prediction: 0.7
Input: [0.0, 0.1], Prediction: 0.6
Input: [0.1, 0.2], Prediction: 0.7
Input: [0.2, 0.0], Prediction: 0.6
Input: [0.6, 0.1], Prediction: 0.7
Input: [0.5, 0.3], Prediction: 0.7
Input: [0.9, 0.1], Prediction: 0.7
Input: [0.1, 0.4], Prediction: 0.7
Input: [0.2, 0.4], Prediction: 0.7
Input: [0.7, 0.0], Prediction: 0.7
Input: [0.6, 0.3], Prediction: 0.7
Input: [0.2, 0.2], Prediction: 0.7
Input: [0.1, 0.0], Prediction: 0.6
Input: [0.2, 0.6], Prediction: 0.7
Input: [0.5, 0.0], Prediction: 0.7
Input: [0.6, 0.4], Prediction: 0.7
Input: [0.4, 0.5], Prediction: 0.7
Enter fullscreen mode Exit fullscreen mode

我们可以看到，我们的网络在数字加法方面表现非常糟糕。25 次预测中只有 2 次正确，而且完全是随机的。这是因为我们还没有对它进行训练。让我们添加训练步骤。



let mut neural_net = NeuralNetwork::new();
// Train for 10000 epochs
neural_net.train(inputs, outputs, 10000);
Enter fullscreen mode Exit fullscreen mode

再次运行它并...



Input: [0.9, 0.1], Prediction: 0.9
Input: [0.5, 0.5], Prediction: 0.9
Input: [0.2, 0.3], Prediction: 0.5
Input: [0.3, 0.6], Prediction: 0.9
Input: [0.1, 0.7], Prediction: 0.8
Input: [0.3, 0.1], Prediction: 0.4
Input: [0.1, 0.5], Prediction: 0.6
Input: [0.9, 0.0], Prediction: 0.9
Input: [0.3, 0.3], Prediction: 0.6
Input: [0.0, 0.1], Prediction: 0.1
Input: [0.1, 0.2], Prediction: 0.3
Input: [0.2, 0.0], Prediction: 0.2
Input: [0.6, 0.1], Prediction: 0.7
Input: [0.5, 0.3], Prediction: 0.8
Input: [0.9, 0.1], Prediction: 0.9
Input: [0.1, 0.4], Prediction: 0.5
Input: [0.2, 0.4], Prediction: 0.6
Input: [0.7, 0.0], Prediction: 0.7
Input: [0.6, 0.3], Prediction: 0.9
Input: [0.2, 0.2], Prediction: 0.4
Input: [0.1, 0.0], Prediction: 0.1
Input: [0.2, 0.6], Prediction: 0.8
Input: [0.5, 0.0], Prediction: 0.5
Input: [0.6, 0.4], Prediction: 0.9
Input: [0.4, 0.5], Prediction: 0.9
Enter fullscreen mode Exit fullscreen mode

哇！它猜对了大约 80% 的答案。还不错。

我们的模型之所以有效，是因为我们试图解决的问题极其简单。能够“记住”更复杂模式的大型神经网络可以拥有跨越多层的数十万个神经元，以及诸如卷积神经网络或循环神经网络等复杂的架构。例如，GPT-3 据称拥有 1750 亿个参数，而其继任者 GPT-4 则据称拥有 1.76 万亿个参数。相比之下，我们的模型只有 3 个参数（2 个权重 + 1 个偏差）。

好了，现在你已经完成了。一个用 Rust 从头开始​​构建的神经网络。

鏂囩珷鏉ユ簮锛�https://dev.to/farshed/building-a-neural-network-in-rust-from-scratch-5bm1
Devto 翻译
PREV
用 Ubuntu 18.04 替换 Windows 10
NEXT
为更轻松的开发项目做好准备……并将本指南提供给您的下一位客户