关于动态规划你需要知道的一切

什么是动态规划以及为什么要关心它？

动态规划

如何解决动态规划问题

示例

更多资源

结论

本文最初发表在我的博客www.yourdevopsguy.com上。

什么是动态规划以及为什么要关心它？

在本文中，我将介绍动态规划的概念，它由理查德·贝尔曼 (Richard Bellman) 在 20 世纪 50 年代开发，是一种强大的算法设计技术，通过将问题分解为更小的问题、存储它们的解决方案，并将它们组合起来以得到原始问题的解决方案来解决问题。

FAANG 编程面试中最难的问题通常都属于这一类。你很可能会在面试中被要求解决这类问题，因此了解这项技术至关重要。我将解释什么是动态规划，提供解决动态规划问题的方案，并通过几个示例帮助你更好地理解何时以及如何应用它。

正如我在上一篇关于编程面试的文章中提到的，我将分享我解决可以用这种方法解决的问题时的思考过程，以便你在遇到类似问题时也能照着做。我不希望你死记硬背任何东西。你需要理解并实践，才能掌握将想法转化为代码的技能。编程不仅仅是学习编程语言。它在于分析问题，考虑不同的解决方案，选择最佳方案，然后用某种编程语言实现它。

动态规划

动态规划是一种解决优化、搜索和计数问题的通用技术，这些问题可以分解为子问题。要应用动态规划，问题必须具备以下两个属性：

• 最佳子结构。
• 重叠的子问题。

最优子结构

如果规模为 n 的问题的最优解可以从规模小于 n 的同一问题实例的最优解中得出，则该问题具有最优子结构。

例如，如果从巴黎到莫斯科的最短路径经过柏林，那么它将由从巴黎到柏林的最短路径和从柏林到莫斯科的最短路径组成。

如果一个问题可以通过组合不重叠子问题的最优解来解决，这种策略就称为分而治之。这就是为什么归并排序和快速排序不属于动态规划问题的原因。

重叠子问题

让我们举一个你可能熟悉的例子——斐波那契数列。斐波那契数列中的每个数字都是前两个数字之和。斐波那契数列可以表示为：

F(0) = F(1) = 1
F(n) = F(n-1) + F(n-2)

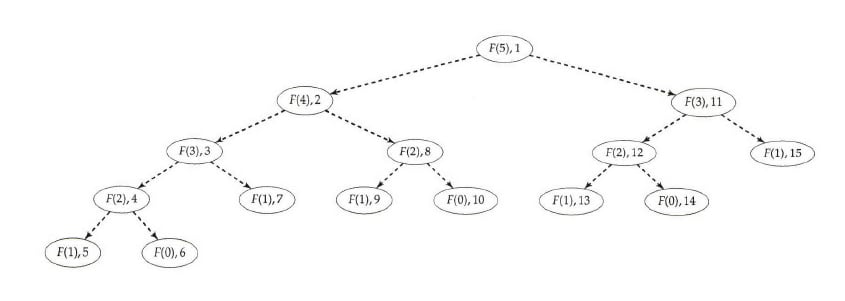
他们说一张图片胜过千言万语，所以这里是（来自编程面试要素）：

要解 F(n)，需要解 F(n-1) 和 F(n-2)，但 F(n-1) 需要解 F(n-2) 和 F(n-3)。F(n-2) 重复出现，源于同一问题的两个不同实例——计算斐波那契数。

这可以用递归函数来表示：

• 为了解决大小为 n 的问题，您可以调用相同的函数来解决相同问题但大小较小的实例。
• 您不断调用该函数，直到遇到基本情况，在此示例中为 n = 0 或 n = 1。

这引出了我们关于递归和动态规划之间的关系。

递归和动态规划

从概念上讲，动态规划涉及递归。您希望基于同一问题的较小实例来解决问题，而递归是在代码中表达此概念的自然方式。与纯递归函数的区别在于，我们将用空间换取时间：我们将存储子问题的最优解，以便能够高效地找到最初想要解决的问题的最优解。

这并不是说你必须使用递归来解决动态规划问题。动态规划解决方案也可以通过迭代的方式进行编码。

自下而上的动态规划

你需要将所有子问题的解决方案（从基准情况开始）填入一个表格，并用它来构建你想要的解决方案。这可以通过迭代的方式完成，使用以下方法之一：

• 多维数组（也是一维数组）——最常用。
• 哈希表。
• 二叉搜索树。

作为存储子问题解决方案的数据结构。

自上而下的动态规划

编写递归算法并添加缓存层以避免重复函数调用。

当我们从例子开始时，这一切都会变得更加清晰。

如何解决动态规划问题

最优子结构和重叠子问题是使用动态规划求解问题必须具备的两个属性。当你的直觉告诉你动态规划可能是一个可行的解决方案时，你需要验证这一点。

让我们试着感受一下哪些类型的问题可以用动态规划来解决。例如：

• 查找前 n 个元素...
• 寻找所有方法...
• 有多少种方式...
• 找到第 n 个...
• 找到最优方法...
• 找到最小/最大/最短路径......

都是有潜质的候选人。

解决动态规划问题的步骤

不幸的是，解决动态规划问题没有通用的秘诀。你需要反复练习才能掌握窍门。不要灰心。这很难，也许是你在面试中遇到的最难的一类问题。这关乎用相对简单的工具对问题进行建模——不需要复杂的数据结构或算法。

我解过很多题，但有时还是觉得很难找到答案。练习得越多，就会越容易。这是最接近动态规划解题秘诀的答案：

• 证明重叠子问题和次优结构属性。
• 定义子问题。
• 定义递归。
• 编写自上而下或自下而上的动态规划解决方案。

复杂度分析因问题而异，但一般来说，时间复杂度可以表示为：

时间 ~ 子问题数量 * 每个子问题的时间

计算自下而上解决方案的空间复杂度很简单，因为它等于存储子问题解决方案所需的空间（多维数组）。

示例

我根据涉及的独立维度数量对一些问题进行了分类。这并非必需，但我发现在设计解决方案时，拥有一个可供遵循的思维模型非常有用。随着你编写的代码越来越多，你会看到一些模式。这就是其中之一（我在其他任何地方都没有找到明确的描述）。如果你觉得有用，就去看看吧。

一维问题

斐波那契

由于您现在已经非常熟悉这个问题，因此我将仅提供递归解决方案：

int fib(int n) {
  if (n == 0 || n == 1)
    return 1;
  else
    return fib(n - 1) + fib(n - 2);
  }

从递归到自上而下通常是机械的：

• 检查所需的值是否已在缓存中。如果是，则返回该值。
• 否则，在返回之前缓存您的解决方案。

int fib(int n) {
  vector<int> cache(n + 1, -1);
  return fib_helper(n, cache);
}

int fib_helper(int n, vector<int> &cache) {
   if(-1 != cache[n])
     return cache[n];

   if (n == 0 || n == 1)
     cache[n] = 1;
  else
    cache[n] = fib_helper(n - 1, cache) + fib_helper(n - 2, cache);
  return cache[n];
  }

这里是自下而上的解决方案，我们根据基准案例构建一个表格，以形成我们正在寻找的问题的解。该表是一个一维数组：我们只需要存储同一问题较小版本的解，就能推导出原始问题的解。

int fib(int n) { 
    vector<int> f(n + 1, 0);  

    f[1] = 1; 

    for(int i = 2; i <= n; i++) 
       f[i] = f[i - 1] + f[i - 2]; 

    return f[n]; 
}

额外空间优化

这种方法可以在内存中进一步优化，而不是时间（有更快的技术来计算斐波那契数，但这是另一篇文章的主题），只需使用 3 个变量而不是数组，因为我们只需要跟踪 2 个值，f(n-1) 和 f(n-2)，即可产生我们想要的输出 f(n)。

int fib(int n) {  
    if (n == 0 || n == 1) 
      return 1;

    //Variables that represent f(n - 1), f(n - 2) and f(n)
    int n1= 1, n2 = 1, f = 0; 

    for (int i = 2; i <= n; i++) { 
        f= n1 + n2; 
        n2 = n1; 
        n1 = f; 
    }
    return f;
}

这是更高级但常见的模式。如果您只需要跟踪以下内容：

• 几个变量，您可能能够摆脱一维数组并将其转换为几个变量。
• 二维矩阵中的几行，您可能能够将其减少为几个一维数组。
• ETC。

降低维度可以提高空间复杂度。现在你可以先不谈这个，但经过一些练习后，尝试自己提出这些优化方案，以提高你分析问题和将想法转化为代码的能力。在面试中，我会选择更简单的版本，只讨论潜在的优化方案，并且只有在编写完“标准”动态规划解决方案后有足够时间的情况下才去实现它们。

爬楼梯

你正在爬楼梯。需要爬 n 级台阶才能到达顶部。每次你可以爬 1 级或 2 级台阶。有多少种不同的方法可以爬到顶部？

例 1：

• 输入：2
• 输出：2
• 解释：有两种方式可以爬到顶部：1 步 + 1 步和 2 步

示例 2：

• 输入：3
• 输出：3
• 解释：有三种方式可以爬到顶部：1 步 + 1 步 + 1 步、1 步 + 2 步和 2 步 + 1 步

解决方案

尝试自己解决这个问题。你或许能想出一个递归的解决方案。仔细阅读我的解释和前面的例子，看看你是否能写出一个自上而下的解决方案。

一点提示：事实上，问题以“有多少种方式”开头，应该已经让你想到了动态规划的潜在候选人。

在这种情况下，你想要到达步骤 N。你可以从步骤 N - 1 或 N - 2 到达步骤 N，因为你可以一次跳过 1 或 2 步。如果你能解决这两个子问题，就能找到整个问题的解。我们把 f(N) 称为到达步骤 N 的方法数。

• 要获得 f(N)，您需要 f(N - 1) 和 f(N - 2)。
• 要得到 f(N - 1)，需要 f(N - 2) 和 f(N - 3)。
• 对于 f(N - 2)，需要 f(N - 3) 和 f(N - 4)。

我不需要继续说下去。你已经看到了：

• 该问题有重叠的子问题：您需要多次计算 f(N - 2)、f(N - 3)、f(N - 4)……
• 该问题呈现最优子结构：通过 f(N - 1) 和 f(N - 2) 的最优解，可以得到 f(N) 的最优解。

这意味着可以使用动态规划来解决它。

我不会为这个问题写代码，因为......我在前面的例子中已经做过了！

您可以在此处编写和测试您的解决方案。

最长递增子数组

给定一个未排序的整数数组，找出最长递增子序列的长度。
[10,9,2,5,3,7,101,18]

对于序列 [2,3,7,101]，输出为 4

解决方案

我们需要求一个长度为 n 的数组的最长递增子序列的长度。这听起来像是一个优化问题，可以作为动态规划的候选题型，所以让我们来试试。假设你已经找到了一个长度为 N 的问题的解——我们称之为 s(n)——并且你向数组中添加了一个额外的元素，称为 Y。你能重用 X 的部分解来解决这个新问题吗？这种思维实验通常能让你对这个问题有更深入的了解。

在这种情况下，您需要知道新元素是否可以扩展现有序列之一：

• 遍历数组中的每个元素，我们称之为 X。
• 如果新元素 Y 大于 X，则可以将序列扩展一个元素。
• 如果我们已经存储了所有子问题的解，那么获取新的长度就很简单了——只需在数组中查找即可。我们可以根据子问题的最优解生成新问题的解。
• 返回新的最长递增子序列的长度。

我们似乎找到了一个算法。让我们继续分析：

• 最优子结构：我们已经验证，可以根据子问题的最优解计算出规模为 n 的问题的最优解。
• 重叠子问题：要计算 s(n)，我需要 s(0), s(1), ..., s(n-1)。反过来，要计算 s(n-1)，我需要 s(0), s(1), ..., s(n-2)。同样的问题需要计算多次。

这是自下而上解决方案的代码。

int lengthOfLIS(const vector<int>& nums) {
        if(nums.empty())
            return 0;

        vector<int> dp(nums.size(), 1);
        int maxSol = 1;

        for(int i = 0; i < nums.size(); ++i){
            for(int j = 0; j < i; ++j){
                if(nums[i] > nums[j]){
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
            maxSol = max(maxSol, dp[i]);
        }
        return maxSol;   
    }

您可以在此处编写和测试您的解决方案。

有多少BST

给定 n，有多少个结构独特的 BST（二叉搜索树）存储值 1 ... n？

例子：

• 输入：5
• 输出：42
• 解释：给定 n = 5，共有 42 个不同的 BST

解决方案

我们来看一下这个例子。假设我们有 1,2,3,4,5 这几个数字。我该如何定义一棵二叉搜索树 (BST)？

我真正需要做的就是从中选择一个数字作为根。假设这个元素是 3，那么结果如下：

• 3 以 root 身份
• 3 左边的数字 1 和 2。
• 3 右边的数字 4 和 5。

我可以针对 (1,2)（我们称之为解 L）和 (4,5)（我们称之为解 R）求解同一个子问题，并计算可以生成多少个以 3 为根（即 L * R 的乘积）的二叉搜索树。如果我们对所有可能的根都执行此操作，并将所有结果相加，就得到了解 C(n)。正如你所见，循序渐进地从一些好的例子入手有助于设计你的算法。

事实上，这就是所有需要做的事情：

• 选择一个元素作为 BST 的根。
• 针对数字 (1 到根 - 1) 和 (根 + 1 到 n) 解决相同的问题。
• 将每个子问题的结果相乘。
• 将其添加到我们的累计总数中。
• 移至下一个根。

事实上，我们并不真正关心数组两侧的数字。我们只需要知道子树的大小，即根节点左右两侧元素的数量。这个问题的每个实例都会产生相同的结果。在我们之前的例子中，L 是 C(2) 的解，R 也是。我们只需要计算一次 C(2)，缓存它，然后重复使用。

    int numTrees(int n) {
        vector<int> dp(n + 1, 0);

        dp[0] = 1;
        dp[1] = 1;

        for(int i = 2; i <= n; ++i){
            for(int j = 0; j < i; ++j){
                dp[i] += dp[j] * dp[i - 1 - j];
            }
        }
        return dp.back();
    }

您可以在此处编码并测试您的解决方案。

二维问题

这些问题通常更难建模，因为它们涉及二维空间。一个常见的例子是迭代两个字符串或在地图中移动的问题。

• 自上而下的解决方案没有太大区别：找到递归并使用缓存（在这种情况下，您的密钥将基于 2 个“索引”）
• 对于自下而上的方法，一个二维数组就足以存储结果。正如我之前提到的，这可能会减少一个或几个一维数组，但不必为此感到压力。我提到这一点只是为了方便你在解决问题时遇到。正如我在另一篇文章中所说，学习是迭代的。首先，专注于理解基础知识，然后一点一点地添加更多细节。

最小路径和

给定一个填充有非负数的 amxn 网格，找到一条从左上角到右下的路径，使路径上所有数字的总和最小化。

注意：在任何时间点您只能向下或向右移动。

例子：

• 输入：[ [1,3,1], [1,5,1], [4,2,1] ]
• 输出：7
• 解释：因为路径 1→3→1→1→1 使总和最小化。

解决方案

最小化应该会让你想到动态规划。让我们进一步分析一下。我们可以从任意索引为 (i,j) 的单元格 C（不在顶部或左侧边界）得到单元格 A = (i-1, j) 和 B = (i,j-1)。由此可见，有些问题需要多次计算。此外，如果已知 A 和 B 的最优解，我们可以将当前单元格的最优解计算为 min(sol(A), sol(B)) + 1 - 因为我们只能从 A 或 B 到达当前单元格，并且需要额外一步才能从这些单元格移动到当前单元格。换句话说，这个问题代表了最优子结构和重叠问题。我们可以使用动态规划。

这是自下而上的解决方案。

    int minPathSum(const vector<vector<int>>& grid) {
        const int nrow = grid.size();

        if(nrow == 0)
            return 0;

        const int ncol = grid[0].size();

        vector<vector<int>> minSum(nrow, vector<int>(ncol, 0));
        minSum[0][0] = grid[0][0];

        for(int col = 1; col < ncol; ++col)
            minSum[0][col] = minSum[0][col - 1] + grid[0][col];

        for(int row = 1; row < nrow; ++row)
            minSum[row][0] = minSum[row - 1][0] + grid[row][0];

        for(int col = 1; col < ncol; ++col){
            for(int row = 1; row < nrow; ++row){
                minSum[row][col] = min(minSum[row - 1][col], minSum[row][col - 1]) + grid[row][col];
            }
        }
        return minSum[nrow - 1][ncol - 1];
    }

边界条件定义在矩阵的边界上。你只能通过一种方式获取边界内的元素：从前一个元素向右或向下移动一个方格。

您可以在此处编码并测试您的解决方案。

背包问题

给定两个整数数组 val[0..n-1] 和 wt[0..n-1]，分别表示与 n 个物品相关的值和权重。同时给定一个整数 W，表示背包容量。找出 val[] 中权重和小于或等于 W 的最大值子集。你不能破坏任何物品，要么选择完整的物品，要么不选择它（0-1 属性）。

解决方案

尝试提出一个递归解决方案。在此基础上，添加一个缓存层，你就得到了一个自上而下的动态规划解决方案！

主要思想是，对于每个项目，我们有两个选择：

• 我们可以将物品添加到袋子中（如果合适），增加总价值，并减少袋子的容量。
• 我们可以跳过该项目，保留相同的值和相同的容量。

遍历完所有组合后，我们只需要选出最大值。虽然速度非常慢，但这是迈向解决方案的第一步。

必须在两个选项之间做出决定（将元素添加到集合中或跳过它）是一种您会在许多问题中看到的非常常见的模式，因此值得了解它并理解何时以及如何应用它。

// Recursive. Try to turn this into a piece of top-down DP code.
int knapSack(int W, int wt[], int val[], int n) { 
     if (n == 0 || W == 0) 
        return 0; 

    if (wt[n - 1] > W) 
        return knapSack(W, wt, val, n - 1); 
    else
        return max(val[n - 1] + knapSack(W - wt[n - 1],  wt, val, n - 1), knapSack(W, wt, val, n - 1)); 
}

这里提出了一种自下而上的解决方案：

// C style, in case you are not familiar with C++ vectors
int knapSack(int W, int wt[], int val[], int n) 
{ 
    int i, w; 
    int K[n + 1][W + 1]; 

    for (i = 0; i <= n; i++) { 
        for (w = 0; w <= W; w++) { 
            if (i == 0 || w == 0) 
                K[i][w] = 0; 
            else if (wt[i - 1] <= w) 
                K[i][w] = max( val[i - 1] + K[i - 1][w - wt[i - 1]], K[i - 1][w]); 
            else
                K[i][w] = K[i - 1][w]; 
        } 
    } 
    return K[n][W]; 
}

最长公共子序列（LCS）

给定两个字符串 text1 和 text2，返回它们最长公共子序列的长度。

字符串的子序列是指在不改变原始字符串的相对顺序的情况下，删除部分字符（可以不删除）生成的新字符串。（例如，“ace”是“abcde”的子序列，而“aec”不是）。两个字符串的公共子序列是指两个字符串共有的子序列。

如果没有公共子序列，则返回 0。

例子：

• 输入：text1 = “abcde”，text2 = “ace”
• 输出：3
• 解释：最长公共子序列是“ace”，其长度为 3。

解决方案

再次，计算最长的X 让我认为动态规划可以在这里提供帮助。

由于你已经对动态规划有一定的经验，我将直接讨论示例中的两个性质。我们将字符串命名为 A 和 B，并将该问题的解命名为 f(A, B)。其思路是判断最后两个字符是否相等：

• 如果是这样，则 LCS 的长度至少为 1。我们需要调用 f(A[0:n-1], B[0:n-1]) 来找到直到该索引的 LCS，并加 1，因为 A[n] 和 B[n] 相同。

• 如果不是，我们就从两个字符串中逐个移除最后一个字符，然后找出哪条路径生成 LCS。换句话说，我们取 f(A[0: n -1], B) 和 f(A, B[0:n-1]) 中的最大值。

• 重叠子问题：让我们看看可以预期哪些调用：("abcde", "ace") 生成 x1 = ("abcd", "ace") 和 y1 = ("abcde", "ac")；x1 将生成 x12 = ("abc", "ace") 和 y12= ("abcd", "ac")；y1 将生成 ("abcd", "ac") 和 ("abcde", "a")。如您所见，相同的问题需要计算多次。

• 最佳子结构：与最长递增子序列非常相似。如果我们在字符串 A' 中添加一个额外的字符，我们就可以快速地从所有缓存的 A 和 B 解法结果中计算出解。

使用例子来证明事情并不是开始数学演示的方式，但对于编码面试来说已经足够了。

int longestCommonSubsequence(const string &text1, const string &text2) {
        const int n = text1.length();
        const int m = text2.length();

        vector<vector<int>> dp(n + 1, vector<int>(m + 1,0));

        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= m; j++){
                if(text1[i-1] == text2[j-1]) 
                    dp[i][j] = dp[i-1][j-1]+1;
                else 
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return dp[n][m];
    }

您可以在此处编码并测试您的解决方案。

更多资源

想了解更多练习，请查看我在上一篇文章中列出的资源。想了解更多动态规划的具体内容，以下视频是个不错的起点。它们讲解得更详细，涵盖了我在文中特意没有讲到的其他问题，以便提供更多选择。

• 麻省理工学院动态规划讲座#1
• 麻省理工学院动态规划讲座#2
• 麻省理工学院动态规划讲座#3
• 麻省理工学院动态规划讲座#4

另外，请查看DP 的维基百科文章。

结论

你需要熟悉这些问题，因为很多其他问题只是这些问题的变体。但不要死记硬背。了解何时以及如何应用动态规划，并不断练习，直到你能够轻松地将你的想法转化为可运行的代码。正如你所见，关键在于方法的严谨性。你不需要深厚的算法或数据结构知识来解决这些问题。数组就足够了。

我还没有完成时间/空间分析。这是给你的练习。如有任何问题或意见，欢迎随时联系我。

附言：希望本文对你有所帮助。如果觉得有用，请点赞并分享，访问我的博客www.yourdevopsguy.com，或者在Twitter上与我们交流。