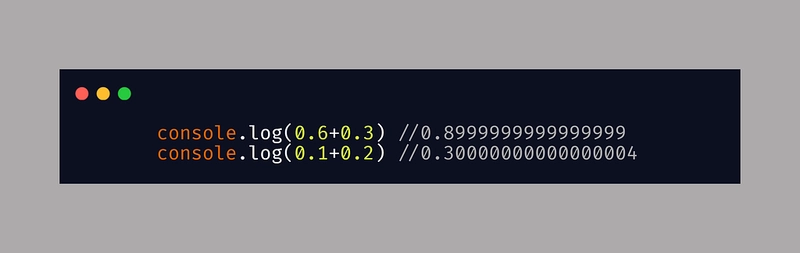
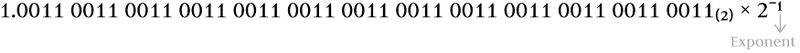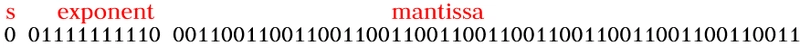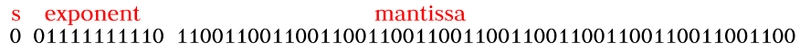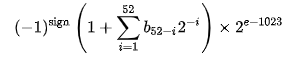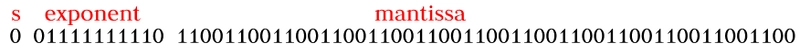解码 JS 中为什么 0.6 + 0.3 = 0.8999999999999999 以及如何解决？

理解 IEEE 754 浮点数，并逐步探索 0.1 + 0.2 等于0.30000000000000004

在Hacktoberfest期间开发一个开源计算器代码库时，我注意到某些小数计算结果与预期不符，例如0.6 + 0.3 的结果不会是 0.9，我怀疑代码是否存在问题。然而，经过进一步分析，我发现这是 JavaScript 的实际行为。于是我深入研究了 JavaScript 的内部工作原理。

在这篇博文中，我将分享我的见解并讨论一些解决这个问题的方法。

在日常数学中，我们知道加0.6 + 0.3等于0.9，对吧？但当我们用计算机计算时，结果却是0.8999999999999999。令人惊讶的是，这种情况不仅仅发生在 JavaScript 中；在许多编程语言中，例如 Python、Java、C，也都存在同样的问题 。而且，这不仅仅局限于这种特定的计算。还有更多小数计算也给出了类似的不太正确的答案。

为什么会发生这种情况？

这都与计算机如何处理浮点数有关。十进制数使用称为 IEEE 754 标准的格式存储在计算机内存中。IEEE 754 标准浮点数是当今计算机上实数最常用的表示形式。该标准包含不同类型的表示，主要包括单精度（32 位）和双精度（64 位）。JavaScript 遵循 IEEE 754 双精度浮点标准。

IEEE 754 双精度浮点格式

双精度由 64 位组成，包括1 位符号位、11 位指数位和52 位尾数（小数部分）。
任何给定的十进制数都仅以这种双精度 IEEE 754 二进制浮点格式存储。计算机系统中有限的 64 位表示法无法准确表达所有十进制值，尤其是那些十进制扩展位数无限的十进制值，这会导致在处理某些二进制数字时结果出现细微差异。

让我们通过一个例子来理解十进制数是如何存储的，并揭示为什么 0.6 + 0.3 等于 0.8999999999999999

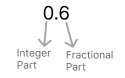
0.6以 IEEE 754 双精度浮点格式表示。

# 步骤 1：将十进制(0.6)₁₀转换为二进制表示base 2

整数部分： 0/2 = 0

小数部分：

反复乘以 2，记录结果的每个整数部分，直到小数部分达到零。

0.1 无法精确地表示为二进制小数。突出显示的部分不断循环，形成了一个无限序列。而且，我们没有得到任何为零的小数部分。

# 步骤 2：规范化
如果一个数字 x 以科学计数法表示，小数点左侧有一个非零数字，则该数字会被规范化。也就是说，强制其尾数的整数部分恰好为 1。

我们根据 IEEE 标准要求调整了序列，包括有限数量的 52 位尾数和舍入。这就是舍入误差出现的原因。

尾数为 0.6

步骤3：调整指数：
对于双精度，-1022 到 +1023 范围内的指数通过加 1023 来获得一个值。

exponent => -1 + 1023 => 1022用 11 位二进制表示该值。

（1022）₁₀ => （010111111110）₂

符号位与正数0相同。 现在，我们已经得到了所有要用 IEEE 754 浮点格式表示的值。0.6(-1)⁰=> 1

在对尾数进行规范化的过程中，前导（最左边）位 1 被删除，它始终为 1，并且仅在必要时将其长度调整为 52 位（这里不是这种情况）。

以 64 位 IEEE 格式表示 0.6。

类似地，使用相同的过程，0.3 表示为：

64位IEEE格式的0.3

# 将两个值相加
1.使指数相等
既然我们已经知道和的值0.6，0.3就需要将它们相加。但在执行此操作之前，请确保指数相同。在这种情况下，它们不相等。因此，我们需要通过将较小的指数与较大的值匹配来调整它们。

Exponent of 0.6=> -1 Exponent of 0.3 => -2，我们必须匹配，0.3因为0.6指数 0.6 大于 0.3。

这里差为1，所以0.3的尾数需要右移1位，指数码增加1，以匹配0.6

将尾数移位 1 位将导致最低有效位丢失，以维持 64 位标准，这可能会引入精度错误。

指数均衡后值为 0.3

2.添加尾数
由于指数现在相等，我们需要对尾数执行二进制加法。

现在的值将是，0; 01111111110; 1.1100110011001100110011001100110011001100110011001100

3.对结果尾数进行标准化并舍入
在这种情况下，尾数已经标准化 [以 1 作为前导位]，因此跳过此步骤。

最后，结果0.6+0.3表示为

64 位 IEEE 浮点表示中的 0.6+0.3 之和

现在，我们得到了0.6 + 0.3以 64 位 IEEE 格式表示的结果，并且机器可以读取。为了便于阅读，我们必须将其转换回十进制。

#将 IEEE 754 浮点表示转换为其十进制等效值

确定符号位： 0 => (-1)⁰ => +1

计算无偏指数：
(01111111110)₂ => (1022)₁₀
2^(e-1023) => 2^(1022-1023) => 2^-1

小数部分：
从尾数最左边的位开始，将各位的值相加，然后乘以 2 的幂。1×2^-1 + 1×2⁻^-2 + 0×2^-3 + ....... + 0×2^-52

通过代入数值并求解方程，我们得到结果0.8999999999999999，并显示在控制台上。[四舍五入]

=> +1 (1+ 1×2^-1 + 1×2⁻^-2 + 0×2^-3 + ....... + 0×2^-52) x 2^-1
=> +1 (1 + 0.79999999999999982236431605997495353221893310546875) x 2^-1
=> 0.899999999999999911182158029987476766109466552734375      
≈ 0.8999999999999999 //numbers are rounded

//Because floating-point numbers have a limited number of digits,
//they cannot represent all real numbers accurately: when there 
//are more digits, the leftover ones are omitted,i.e. the number is rounded

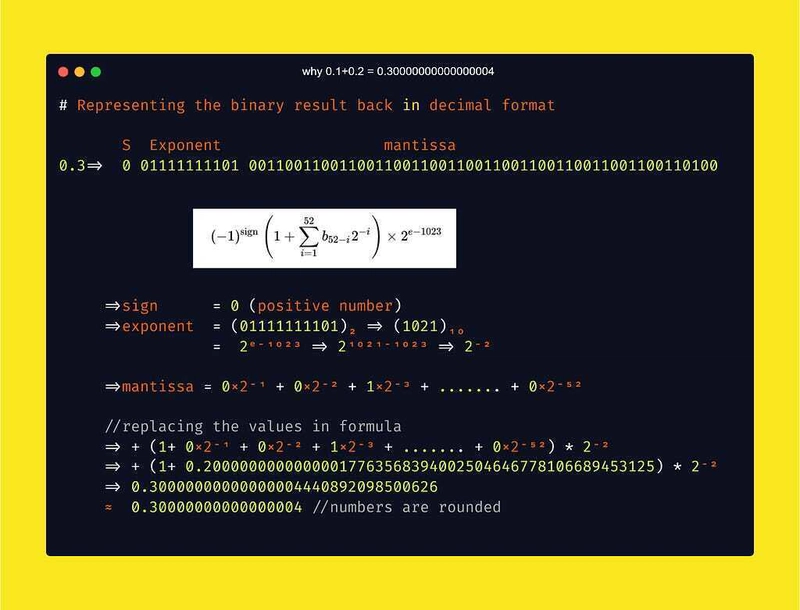
让我们再探讨一个例子，以更深入地理解众所周知的表达式0.1 + 0.2 = 0.30000000000000004。

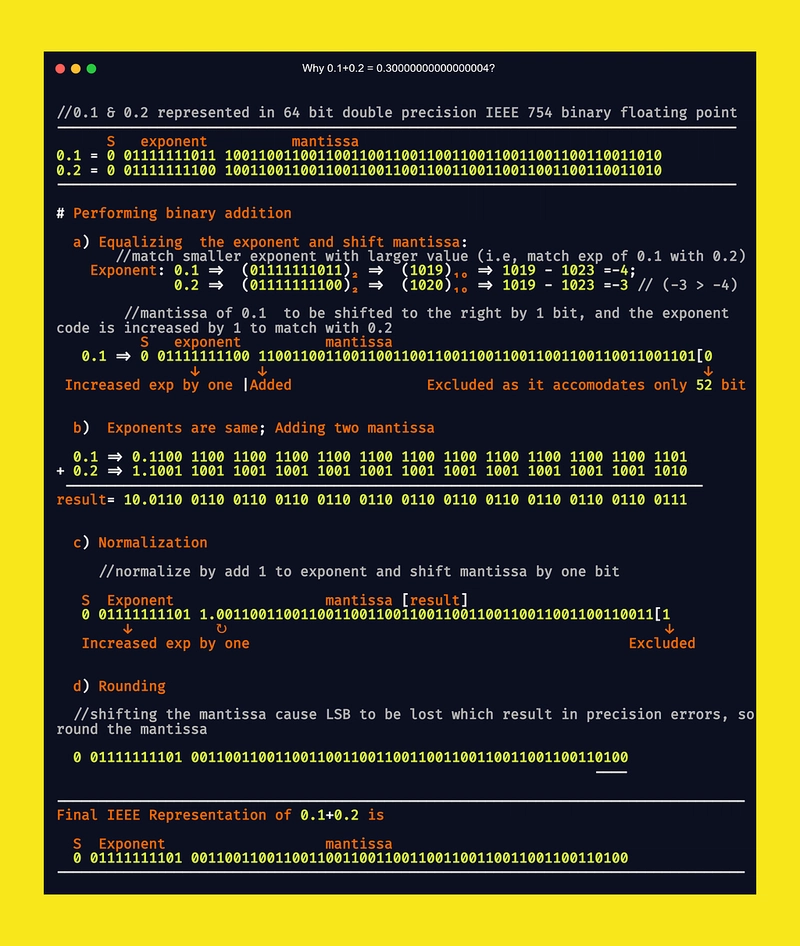将 64 位 IEEE 754 二进制浮点值 0.1 和 0.2 相加

将结果转换回十进制

如何解决？

让我们看看在使用处理货币或财务计算的应用程序时如何获得准确的结果，因为精度至关重要。

i）内置函数：toFixed（）和toPrecision（）

• toFixed()将数字转换为字符串，并将字符串四舍五入到指定的小数位数。
• toPrecision()将数字格式化为特定的精度或长度，并在需要时添加尾随零以满足指定的精度。parseFloat ()用于从数字中删除尾随零。

const num1 = 0.6;
const num2 = 0.3;
const result = num1 + num2;

const toFixed = result.toFixed(1); 
const toPrecision = parseFloat(result.toPrecision(12));

console.log("Using toFixed(): " + toFixed); // Output: 0.9
console.log("Using toPrecision(): " + toPrecision); // Output: 0.9

限制
toFixed() 始终将数字四舍五入到给定的小数位，但在所有情况下可能并非都对齐。toPrecision() 也类似，对于非常小或非常大的数字，它可能不会产生准确的结果，因为它的参数应该在 1-100 之间。

//1. Adding 0.03 and 0.255 => expected 0.283
console.log((0.03 + 0.253).toFixed(1)) // returns 0.3

//2. Values are added as a string
(0.1).toPrecision()+(0.2).toPrecision() // returns 0.10.2

ii) 第三方库

有各种各样的库，例如math.js、decimal.js、big.js，可以解决这个问题。每个库的功能都遵循其文档。这种方法相对来说更好一些。

//Example using big.js
const Big = require('big.js');

Big.PE = 1e6; // Set positive exponent for maximum precision in Big.js

console.log(new Big(0.1).plus(new Big(0.2)).toString()); //0.3
console.log(new Big(0.6).plus(new Big(0.3)).toString()); //0.9
console.log(new Big(0.03).plus(new Big(0.253)).toString()); //0.283
console.log(new Big(0.1).times(new Big(0.4)).toString()); //0.04

结论

IEEE 754 标准用于存储十进制数，可能会导致细微的差异。可以使用各种库来获得更精确的结果。请根据应用需求选择合适的方法。其他语言中也存在等效的库，例如Java 的BigDecimal和 Python 的Decimal。

参考文献：

什么是双精度浮点格式
将十进制转换为 IEEE 64 位双精度
将 IEEE 64 位双精度转换为十进制
全精度计算器
https://zhuanlan.zhihu.com/
https://0.300000000000000004.com/

---

感谢阅读。欢迎留言评论😊。希望这篇文章对你有帮助。你可以在领英 上联系我。这里还有其他几篇文章可以查看。

• 首次尝试开源贡献：Hacktoberfest'23 之旅
• 如何在开发工具中隐藏 React 源代码 [3 种不同的方法]
• 如何在 Windows 中使用 Create React App 创建和设置 React 项目？