MLS.1 线性回归
文章中讨论的主题的源代码可以在https://github.com/ML-Scratch/ML_Code_From_Scratch找到。
线性回归是一种非常基本的监督学习模型。当特征向量和目标之间存在线性关系时,或者简单地说,当我们试图预测的输入和输出之间存在线性关系时,就会使用线性回归。线性回归是许多机器学习爱好者的起点,理解这个模型可以极大地帮助我们掌握机器学习中更复杂的模型。
何时应使用线性回归?
顾名思义,线性回归涉及通过数据拟合最佳拟合直线。考虑一个包含二手车及其售价信息的数据集。例如,它由汽车行驶的公里数和售价组成。人们可能意识到,行驶公里数和售价之间可能存在线性关系。
像上图这样的数据可视化清楚地表明,直线可以拟合这类数据。还要注意的是,在大多数情况下,不可能拟合出一条穿过数据集所有点的直线。我们能做的最好的就是拟合一条看起来像穿过大多数点的直线,我们将在接下来的部分中看到如何做到这一点。一旦我们拟合出一条穿过这些数据的直线,即生成一个直线方程,我们就可以通过将汽车行驶的公里数代入直线方程来预测价格。
理解数学
线性回归背后的数学原理并不复杂。为了简单起见,我们假设数据集中只有一个特征,即行驶里程(我们称之为 X),以及一列汽车的售价(我们称之为 Y)。
我们的任务是创建一个类似 的线性方程。当将数据集中的 (即行驶公里数)Y = mX + c的值代入该方程时,它应该计算出(即预测售价),该值要么等于数据集中的售价值,要么是某个足够接近的值。XY
你可能会想到,上述直线方程中的变量是和,m它们c只是直线的斜率和y截距。请记住,在我们的例子中,X和Y不是变量,因为它们只是数据集中的常量,我们将用它们来创建最佳拟合线。
因此,我们现在的工作是找出正确的m和c值,以便我们可以绘制一条穿过数据集中大多数点的理想直线。
让我们稍微修改一下上面的等式, 其中和。Y = θ0 + θ1Xθ0 = cY = θ1 = m
如何判断一条线是否足够好?
现在我们理解了直线方程,那么我们应该如何判断我们使用的直线方程是否是最佳拟合线呢?一个显而易见的方法是将直线与数据集进行对比,然后直观地判断。
然而,对于包含大量特征的大型数据集来说,这实际上是不可能的,现实世界中的大多数数据集通常都是这种情况。因此,我们使用一个称为成本函数的简单数学公式来判断给定的直线是否与数据拟合良好。
考虑以下迷你数据集:
| 序号 | Km的旅行 | 价格 |
|---|---|---|
| 1 | 1000 | 2.1 |
| 2 | 2000 | 1.7 |
假设我们从和的随机值开始。让我们按照数据集中的第一个示例进行代入。θ0 = 10θ1 = 20X = 1000
Y = 10 + 20(1000)Y = 20010
根据上述公式,预测值为 20010 卢比,而根据数据集的售价为 200000 卢比。这无疑是一个错误的预测。该预测的糟糕程度,或者从技术上讲,误差Ŷ,是预测值(用 表示)与实际值(用 表示)之间的差值Y。
其中预测值为Ŷ = 20010实际值(或来自数据集的值)Y = 210000。
两个变量的成本函数和分别表示为和,如下所示θ0θ1J
成本函数计算数据集中每个示例的误差平方,将其相加,然后将该值除以数据集中的示例数(用表示m)。
该成本函数有助于确定最佳拟合线。
注意:除以 2 是为了简化涉及一阶微分的计算
找到最佳拟合线
现在我们已经定义了成本函数,我们必须利用它来调整参数,使成本函数值最小。我们使用一种称为梯度下降的技术来最小化成本函数的值。θ0θ1
梯度下降法会对现有的和值进行细微的调整,使其成本函数值越来越小。对和的调整如下。θ0θ1θ0θ1
其中j = 0或j = 1
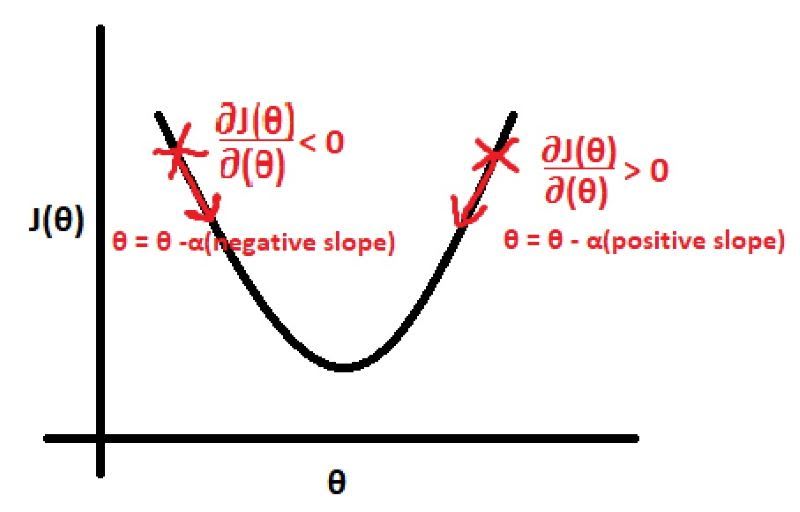
让我们尝试去理解,这次更新意味着什么?θ0θ1
该等式的微分部分决定了我们是否需要增加或减少该值。如果该微分是正值,则减小;如果该微分是负值,则减小,正如从上述等式可以看出的那样。θjθjθj
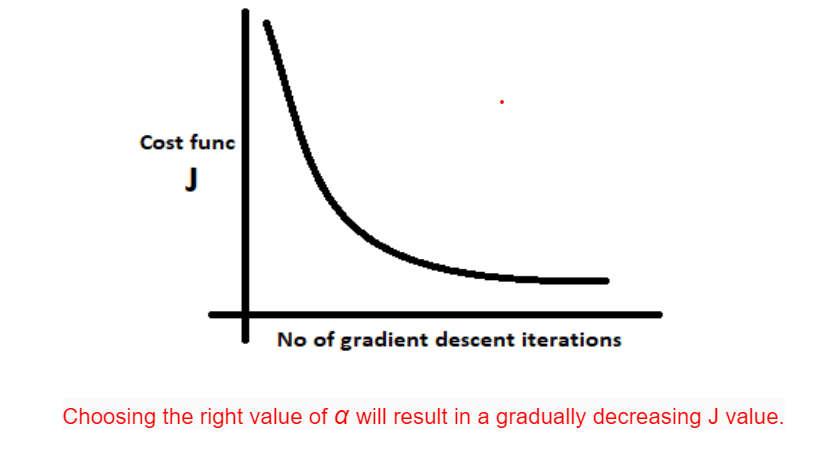
现在我们知道了是否需要增加或减少,接下来我们必须确定应该改变多少。这就是学习率所指示的。值越大,更新量就越大,反之亦然。值不应太小,因为这会导致收敛到最佳拟合线的速度非常慢;也不应太大,因为我们可能会错过导致最佳拟合线的 值。θjθjααθjαθj
一组更新称为梯度下降的迭代。θj
这个更新过程重复进行,直到成本函数值基本保持不变。
经过足够次数的梯度下降迭代后,我们可以通过绘制该直线与数据集中数值的对比图来直观地检查其性能。如果一切顺利,你应该会得到一条相当不错的直线。现在,你可以使用这条直线方程对任何给定X值(或行驶的公里数)进行预测。
优点
- 空间复杂度非常低,只需在训练结束时保存权重即可。因此,它是一种高延迟算法。
- 很容易理解
- 良好的可解释性
- 特征重要性是在模型构建时生成的
- 借助超参数 lambda,你可以处理特征选择,从而实现降维
- 超参数数量较少
- 可以通过正则化来避免过度拟合,这是直观的
- Lasso 回归可以提供特征重要性
缺点
- 该算法假设数据在现实中呈正态分布,但事实并非如此
- 在建立模型之前应该避免多重共线性。
- 容易出现异常值。
- 输入数据需要缩放,并且有多种方法可以做到这一点。
- 当假设函数是非线性的时候,可能效果不佳。
- 复杂的假设函数确实很难拟合。虽然可以使用二次特征和高阶特征来实现,但这些特征的数量会随着原始特征数量的增加而迅速增长,计算成本可能会非常高。
- 由于存在大量特征,因此容易出现过度拟合。
- 可能无法处理不相关的功能
到目前为止一切顺利,我们已经了解了线性回归的概述,我们的下一篇文章将围绕线性回归中涉及的数学概念展开。
继续阅读📝
贡献者
本系列文章的完成得益于以下各方的帮助:
- Pranav(@devarakondapranav)
- Ram(@r0mflip)
- 德维卡(@devikamadupu1)
- Pratyusha(@prathyushakallepu)
- 普拉奈(@pranay9866)
- 苏巴斯里(@subhasrir)
- 拉克斯曼(@lmn)
- Vaishnavi(@vaishnavipulluri)
- 苏拉杰(@suraj47)
 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com