我测试了 OpenAI 的 o1-preview 几个小时——你不会相信我发现了什么🤯

TL;DR

除非您一直生活在与世隔绝的地方，否则您可能已经听说过 OpenAI 的重磅发布：o1-preview。

作为一名人工智能爱好者和人工智能初创公司Composio的成员，该公司的主要业务是人工智能模型，我花了数小时通过无数的提示对该模型进行测试，以了解它有多棒。

它是否名副其实，还是又一次被过度炒作？我们拭目以待。

我在以下平台上测试了该模型：

推理
数学
编码
创意写作

以下是我对其表现的详细分析。

什么是 o1-preview？

o1-preview 是 OpenAI 的新系列 AI 模型，能够在响应查询之前进行“思考”和“分析”。

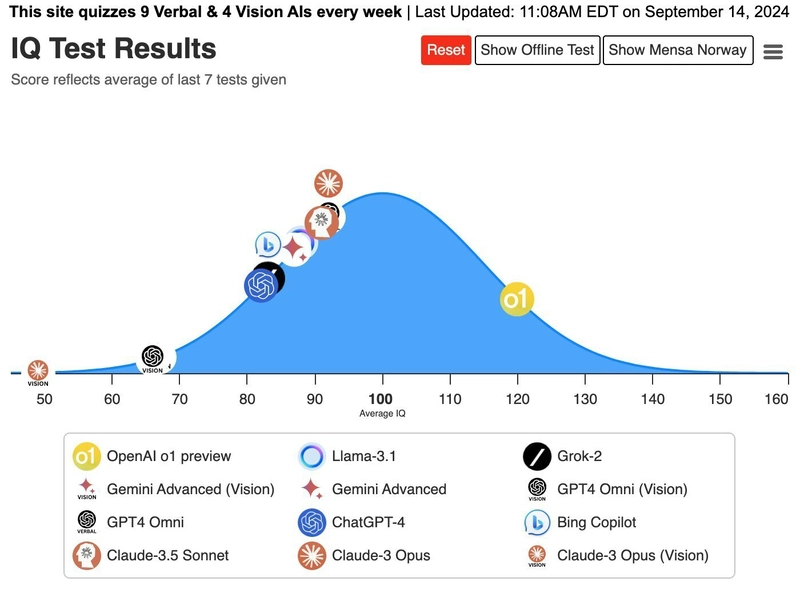
据报道，该模型在 IOI（国际信息学奥林匹克）和 Codeforces 中取得了优异成绩，经测试其智商达到 120（基于挪威门萨测试）。

该模型的思考部分基于对海量思维链数据集的强化学习。这使得模型能够模拟思考过程，从而获得更好的解决方案。

关于 o1-preview 原生 CoT 的一些话

在开始讨论之前，先说说我对 o1 原生思维链能力的感受。

推理能力显著提高。
有时，它在完成思考过程后无法输出答案。我想知道这是否与模型有关。有几次，即使CoT轨迹有些不一致，它也能正确回答。同样，我不确定这是否在意料之中，而且无法知道原因。
CoT 上的强化学习有效，不会卡住或崩溃，这是一个显著的进步。

推理

逻辑推理是它比现有模型表现更佳的地方，这得益于其原生的思维链式思维过程。这正是该模型的全部卖点，而且它的表现丝毫不令人失望。它完全超越了所有模型。

让我们从一个基本的推理问题开始。

#1. 统计回复中的字数

提示：你对这个提示的回答有多少个字？

我尝试用 GPT-4o 和 Sonnet 3.5 运行同样的提示，但都失败了。不过，O1 模型第一次尝试就成功了。

让我们给它另一个任务。

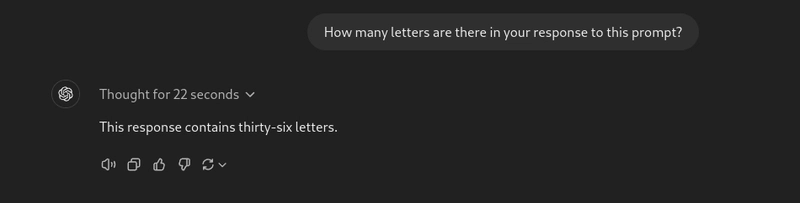
提示：你对此提示的回答有多少个字母？

它无需任何工具就能完美地完成所有操作。与之前的型号不同，它不会将特殊字符和数字误认为字母。

让我们进一步探讨一下。

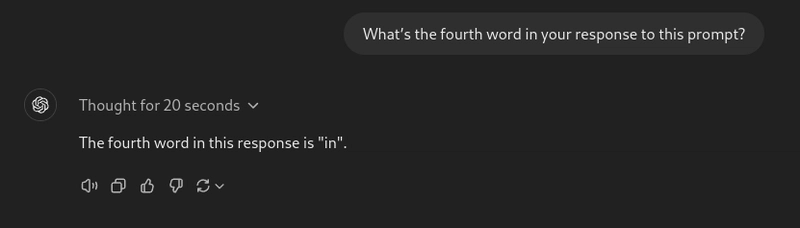
提示：你对此提示的回答的第四个词是什么？

o1-preview 模型在第一次尝试时就成功了，而 GPT-4o 和 Sonnet 即使使用工具也未能做到这一点。

#2. 计算“Strawberry”中字母“r”的数量

这是一次令人兴奋的测试，因为除了 Sonnet 3.5 之外，早期的模型都没有能够在第一次尝试中正确完成，而围绕该模型的大部分兴奋点在于它能够成功做到这一点。

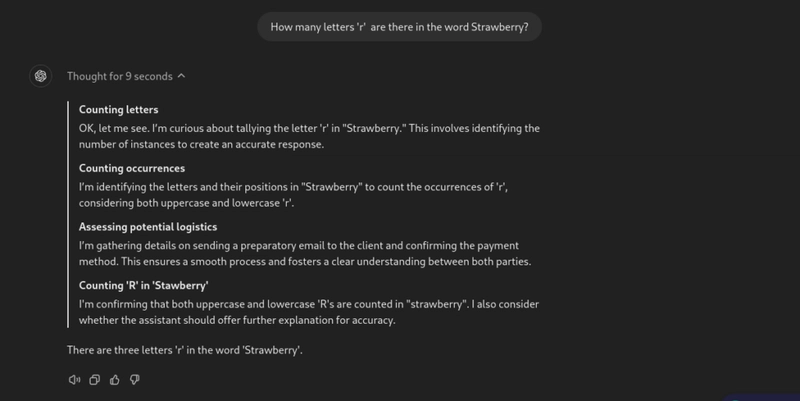
提示：单词“strawberry”中有多少个字母“r”？

令我们惊讶的是，该模型第一次尝试就能够实现当前状态。

您可以观察模型为了得到答案而经历的整个思维序列。

这变得越来越令人兴奋，所以让我们提高问题的难度。

#3. C 在房间里做什么？

这次，我问了一个更棘手的推理问题。

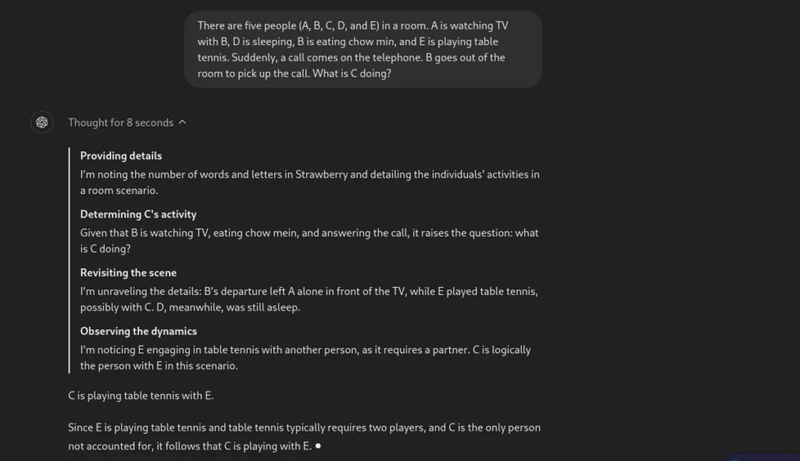
提示：五个人（A、B、C、D、E）在一个房间里。A 和 B 一起看电视，D 在睡觉，B 在吃炒面，E 在打乒乓球。突然，电话铃响了。B 走出房间接电话。C 在做什么？

GPT-4o 完全失败了。以下是它的回应。

现在，让我们看看 o1-preview 的响应。

太棒了！模型能够抓住问题的细微之处，并成功回答问题。

#4. 谁在车祸中丧生了？

让我们看看另一个推理任务。

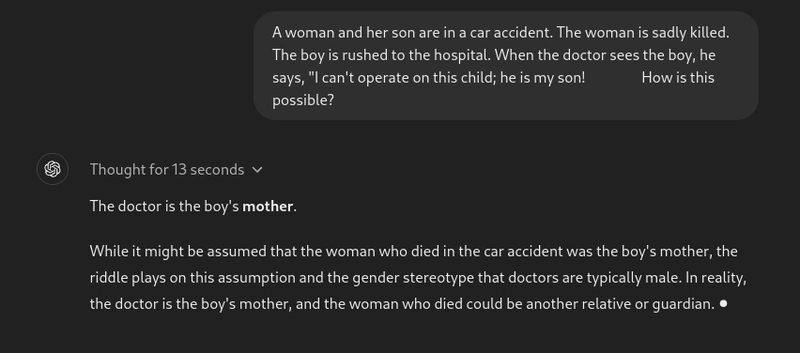
提示：一位妇女和她的儿子遭遇车祸。妇女不幸身亡。男孩被紧急送往医院。医生看到男孩后说：“我不能给这个孩子做手术；他是我的儿子！这怎么可能？”

这是一个经典的推理问题。

#5. 农夫和羊的问题

这道题很简单，却能轻易地把任何LLM（法学硕士）都难倒。让我们看看o1-preview的成绩如何。

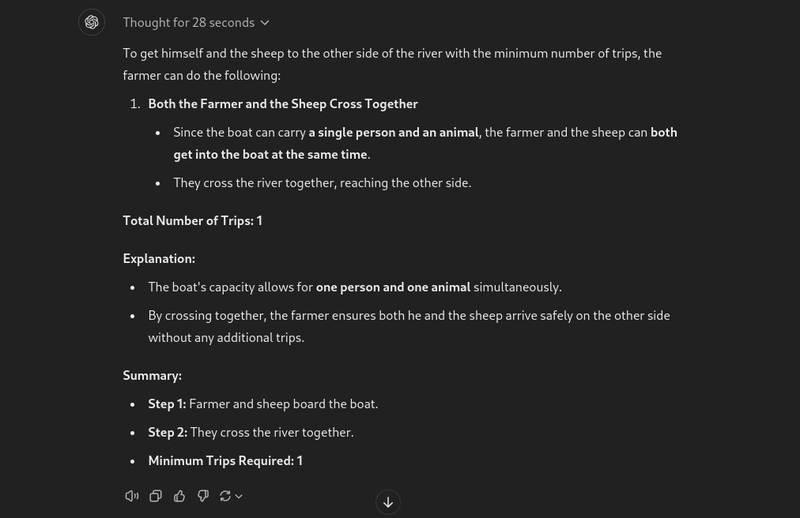
提示：一位农夫和羊站在河的一边。一艘船只能载一人和一头羊。农夫怎样才能用最少的行程，把羊送到河的对岸？

嗯，我看到的第一个模型无需人工协助就能解决这个问题。

推理总结

O1系列无疑是对前几代机型的重大升级。它在复杂推理方面表现出色，但仍有改进空间。它并非“思考”，而是通过原生思维链来提升推理能力。

数学

考虑到它的推理能力，我几乎确信它会突破数学，而且它也没有让人失望。

让我们向它提出一些数学问题。这些问题是其他模型无法正确回答的。

#1. 找到平行四边形的第四个可能顶点

让我们从一个代数问题开始。

提示：如果平行四边形的三个角分别为 (1,1)、(4,2) 和 (1,3)，那么所有可能的第四个角是什么？

这是 Gilbert Strang 的《线性代数》中的一个问题。由 Twitter 上的 @allgarbled 提供。

该模型第一次尝试只能找到两个可能的顶点。但是，当受到推动时，它就能正确回答所有三个可能的顶点。

#2. 求整数之和

我们再来试试另一道数学题。这次是代数。

提示：两个小于100的正整数的最大公约数是3。它们的最小公倍数是其中一个整数的12倍。这两个整数的最大和是多少？

这是一个数学数据集问题，其他模型通常无法正确解决。

然而，o1-preview 却一次性得出了正确答案，耗时 37 秒。这表现简直惊艳。

#3. 三角问题

我们再举一个例子；这次是一道三角问题。

提示：一辆汽车以匀速直线驶向一座垂直塔的底部。从车上观察塔顶，仰角从45°变为60°。这辆车需要多长时间才能到达塔底？

所有之前的模型都需要借助外部帮助才能正确解答这个问题。然而，o1-preview 却正确解答了这个问题。

#4. 黎曼假设

在此之前，我并不知道黎曼猜想是什么。许多人要求该模型解决这个猜想，但至今仍未得到解决。而该模型不出所料地没有尝试去解决它。

我们距离实现这个目标还很遥远，但最终我们将会实现这个目标。

数学总结

这比所有法学硕士（LLM）课程都有显著的进步。它能正确回答许多难题。不过，有时需要人工协助才能得到完整的答案，这也很正常。

编码

现在让我们来检查一下 o1-preview 的编码能力。

我们以“超级英雄”问题这个相对棘手的动态规划问题来测试一下最近一些竞争性编程比赛中出现的模型。

这个问题不太可能受到污染，这意味着模型不太可能针对该问题进行训练。

问题

You are given a 0-indexed integer array nums representing the strength of some heroes. The power of a group of heroes is defined as follows:

Let i0, i1, ... ,ik be the indices of the heroes in a group. Then, the power of this group is max(nums[i0], nums[i1], ... ,nums[ik])2 * min(nums[i0], nums[i1], ... ,nums[ik]).
Return the sum of the power of all non-empty groups of heroes possible. Since the sum could be very large, return it modulo 109 + 7.



Example 1:

Input: nums = [2,1,4]
Output: 141
Explanation: 
1st group: [2] has power = 22 * 2 = 8.
2nd group: [1] has power = 12 * 1 = 1. 
3rd group: [4] has power = 42 * 4 = 64. 
4th group: [2,1] has power = 22 * 1 = 4. 
5th group: [2,4] has power = 42 * 2 = 32. 
6th group: [1,4] has power = 42 * 1 = 16. 
7th group: [2,1,4] has power = 42 * 1 = 16. 
The sum of powers of all groups is 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141.

Example 2:

Input: nums = [1,1,1]
Output: 7
Explanation: A total of 7 groups are possible, and the power of each group will be 1. Therefore, the sum of the powers of all groups is 7.


Constraints:

1 <= nums.length <= 105
1 <= nums[i] <= 109

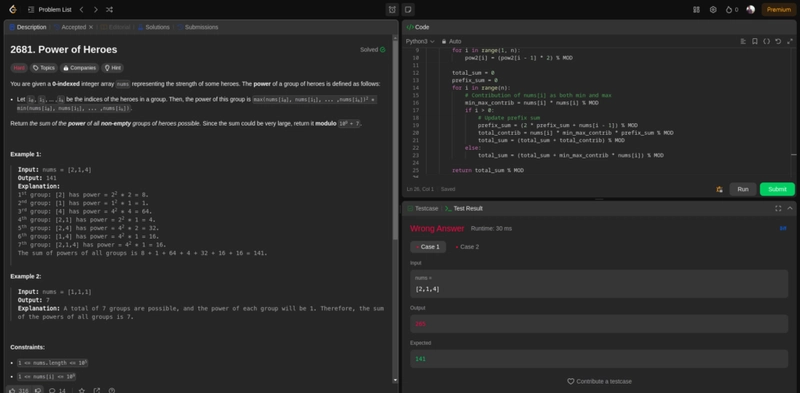
这是之前只有 Claude 3.5 Sonnet 能答对的题目之一，o1-preview 模型花了 91 秒才得出一个无法通过第一个测试用例的解决方案。我试了两次，但都没成功。

这是输出代码。

class Solution:
    def sumOfPower(self, nums):
        MOD = 10**9 + 7
        nums.sort()
        n = len(nums)

        # Precompute powers of 2 modulo MOD
        pow2 = [1] * n
        for i in range(1, n):
            pow2[i] = (pow2[i - 1] * 2) % MOD 

        total_sum = 0
        prefix_sum = 0
        for i in range(n):
            # Contribution of nums[i] as both min and max
            min_max_contrib = nums[i] * nums[i] % MOD
            if i > 0:
                # Update prefix sum
                prefix_sum = (2 * prefix_sum + nums[i - 1]) % MOD
                total_contrib = nums[i] * min_max_contrib * prefix_sum % MOD
                total_sum = (total_sum + total_contrib) % MOD
            else:
                total_sum = (total_sum + min_max_contrib * nums[i]) % MOD

        return total_sum % MOD