7 分钟内理解大 O 符号

大 O 符号是一个经常被开发人员完全忽略的概念。然而，它却是一个基础概念，不仅实用，而且易于理解。与普遍的看法相反，你不需要成为数学迷就能掌握它。我敢打赌，7 分钟内你就能理解一切。

什么是大 O 符号？

大 O 符号（或算法复杂度）是衡量算法性能的标准方法。它是一种判断代码有效性的数学方法。我之前提到“数学”这个词的时候，把所有人都吓跑了。再说一次，你不需要对数学有热情就能理解和使用这个符号。

这种表示法可以让你测量算法相对于输入数据的增长率。它描述了代码性能的最坏情况。今天我们不讨论空间复杂度，只讨论时间复杂度。

这并不是在函数前后放置一个计时器来查看它需要多长时间。

问题在于，计时器技术既不可靠也不准确。使用简单的计时器，算法的性能会因多种因素而发生巨大变化。

• 您的机器和处理器
• 您使用的语言
• 运行测试时机器的负载

大 O 符号解决了所有这些问题，并使我们能够可靠地衡量您编写的所有代码的效率。大 O 是“数量级”的简称。

理解这一点至关重要。你不能直接用秒来衡量算法的速度。你应该用完成算法所需的操作数来衡量算法的增长率。在开发人员中衡量性能时，应该使用大 O 符号。

不服气？好吧，让我们来想象一下现实生活中的情况！

这可能发生在你身上

想象一下，你正在努力工作，有一天你被要求编写一个函数，返回从 1 到传入参数的数字之间所有数字的和。更确切地说，就是实现这样的行为。

n = 3

output = getSum(n)

print(output)
# will print : 6  because 1 + 2 + 3 = 6

你首先想到的可能是写一个简单的循环，逐个累加这些数字。我会用 Python 给出一些例子，但我们并不关心具体是什么语言。它适用于任何语言。

def getSum(n):
    sum = 0

    for number in range(1, n + 1):
        sum += number

    return sum

果然成功了。你输入 3 启动函数：立刻就得到了正确的结果。太棒了！你正在推送到 prod，然后漫不经心地喝着咖啡。

几天后，有人直接联系你，告诉你系统变得超级慢。这是因为你的函数。你的函数处理时间长达15秒以上！它经常会阻塞整个系统几秒钟。

慌了！你查看日志，发现输入变成了巨大的数字。有时，你的函数输入会高达 10 亿。不得不让其他开发人员介入。你的函数被替换了，一切恢复正常。你查看新的代码，就看到了。

def getSum(n):
    return n * (n + 1) / 2

这个函数可以立即解决问题，即使输入高达 1 万亿。你在 Slack 上问了实现这个函数的开发者，他的回答让你更加困惑。

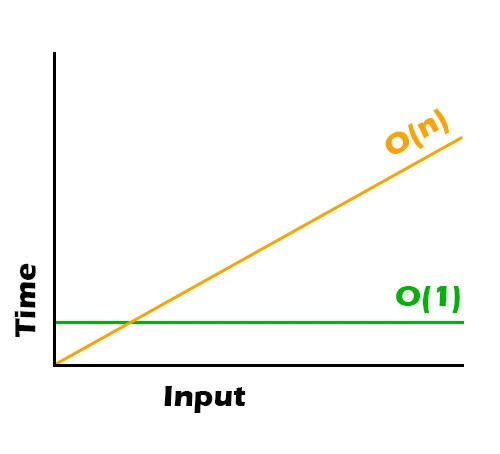
你好！你的解法虽然线性趋近于 O(n)，但输入量很大。我找到了一个常数解法，时间复杂度为 O(1)。现在，无论输入量有多大，它都会很快。

你看着屏幕，有一个问题让你着迷。

它是如何工作的？

正如我所说，关键在于评估机器需要执行多少次运算才能解决你的问题。对于你的解决方案，需要执行很多运算。

def getSum(n):
    sum = 0  <-- assignment

    for number in range(1, n + 1): <-- addition + range
        sum += number <-- n additions + n assignments

    return sum

我们不会对操作次数进行精确计算，因为我们不在乎具体数字。我们想要根据输入参数得出所需操作次数的趋势。现在最应该令人震惊的是第 4 行和第 5 行的循环。

解决问题所需的运算量将乘以输入的大小。数量级与函数输入的数字 n 直接相关。因此，函数的线性趋势为 O(n)。

输入是10亿？机器需要进行1,000,000,000 * 次运算。

其他功能则不是这样。

def getSum(n):
    return n * (n + 1) / 2 <-- three operations

使用此解决方案，解决问题的运算量不会随着输入的增加而增加。无论输入如何，您的数量级始终是三个运算。因此，您的函数具有 O(3) 的恒定趋势，简化为 O(1)。如果您画一幅图，它看起来就像这样。

你开始明白为什么记住这个概念很重要了。显然，这种表示法还有其他应用场景。我们来快速看一下。

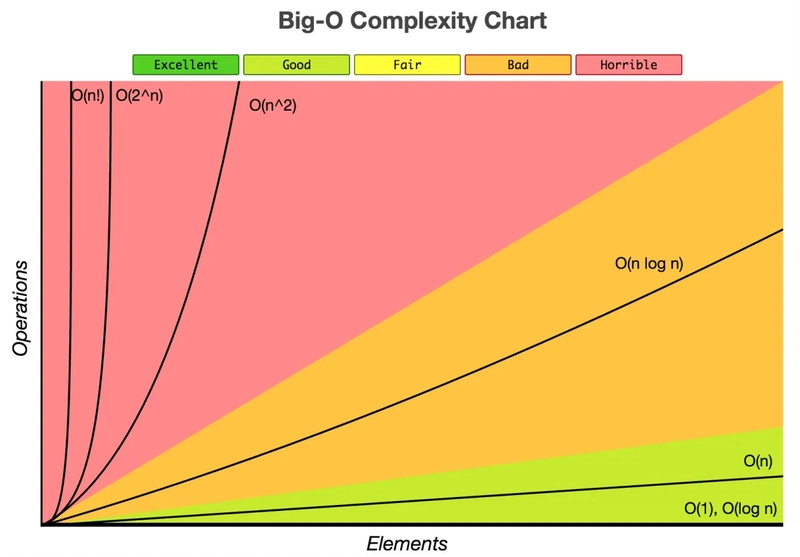
大 O 符号示例

常数复杂度 O(1)

常数复杂度O(1)无论输入如何变化，每次所需的操作次数都相同。

def exempleO1(n):
    print(n + n)

对数复杂度O(log(n))

如果你不了解数学中对数的概念，那么对数复杂度O(log(n))会更难理解。简而言之，对数趋势与指数趋势相反。指数趋势会随着时间的推移成倍增长，算法的性能也会随之下降，而对数趋势则会呈除法。

def exempleOlogn(n):
    i = 1

    while(i < n):
        i = i * 2
        print(i)

二分查找算法正是根据这一趋势而工作的。

线性复杂度 O(n)

线性复杂度O(n)与输入的大小成正比。运算次数会随着输入数量的增加而增加。最简单的例子是一个简单的循环。

def exempleOn(n):
    for number in range(n):
            print(number + 1)

线性对数复杂度O(n log(n))

线性复杂度O(n log(n))使用与对数复杂度相同的“分而治之”方法，只是它对输入 n 的每个元素都这样做。

def exempleOlogn(n):
    i = 1
    for number in range(n):
        while(i < n):
            i = i * 2
            print(i)

合并排序算法正是顺应了这一趋势。

合并排序算法正是顺应了这一趋势。

二次复杂度 O(n²)

二次复杂度O(n²)将演变为输入的平方。运算次数也将增长到输入的平方。两个嵌套循环就是这种趋势的完美例证。

def exempleOn2(n):
    for number in range(n):
        for number in range(n):
            print(number + 1)

最著名的排序算法（快速排序、冒泡排序、插入排序）都有这种趋势。

还有很多其他的我就不说了。如果你想全部看完，维基百科页面很有意思。

另外，看看这个简短的 YouTube 视频，它对理解简化符号书写的规则非常有用。例如，为什么 O(3) 简化为 O(1)？为什么两个非嵌套循环的复杂度仍然是 O(n)？就像你的专业领域中的任何学科一样，它涉及知识的海洋。

最后，我们将讨论为什么这一切都很重要。

为什么这很重要？

我看到一些开发人员使用小批量软件，确信这些对他们毫无用处。甚至一些拥有300年经验的开发人员也不需要这些东西。

大 O 符号快速解答了每个开发人员在工作中都应该问自己的一个问题：我的解决方案的扩展性如何？无论你的数据量是否巨大，这都无关紧要。重要的是，你必须了解解决方案的极限，以便估算系统的极限。

然后，通过理解这个概念，你将拥有一种与其他开发人员讨论的标准语言。这对于比较解决方案、做出权衡以及简单地交换技术信息都很重要。

如果你不明白我们在说什么，那你就有障碍了。就我个人而言，在我职业生涯初期的采访中也遇到过这种情况。我完全不知道他在说什么，当时我非常恐慌。

有了这些基本的理解，我解决问题的方式就改变了。作为一名开发人员，编写优化的代码至关重要。

最后但同样重要的是，这些概念能让你快速发现运行缓慢的系统出了什么问题。很多时间都花在阅读和修复其他开发人员的代码上。所有这些都能让你更快地找到并优化运行缓慢的代码。

结语

我希望这篇关于大 O 符号的介绍能让你了解更多信息。了解这个概念对于更好地优化你的代码至关重要。总的来说，随着你的职业生涯发展，它会对你越来越有用。