正则表达式：它们如何工作？

这最初发布在我的个人博客上。

亲爱的程序员！我觉得我们该聊聊正则表达式了。你觉得呢？

是的，我知道你了解它们，并且能够在大多数实际情况下使用它们。太棒了！我认识一些程序员，对他们来说，更复杂的正则表达式简直就是黑魔法。即使他们可能有好几年的经验。但我不想向你灌输如何构建一个正则表达式¹来解决你的问题。我打算解释它们内部是如何工作的，以及它可能对我们造成什么后果。

那么，我们从哪里开始呢？其实，这得从数学说起。具体来说，要从一种叫做有限自动机的数学概念开始。虽然它的正式定义听起来可能有点吓人，但它其实是一个相当简单的想法。而且它很容易被形象化，所以不用担心。

有限自动机是一组状态（通常称为q1、q2、q3等），通过转换连接。转换类似于有向图中的边：它们是单向的（因此用箭头表示），并且都分配有标签。其中一个（且只有一个）状态被标记为初始状态或起始状态（通常也称为q0），并且至少有一个状态是最终状态或接受状态。

我们说自动机建立在字母表（alphabet）上，字母表是转换标签中允许使用的字符集合。我们还有一个输入，它只是一个字符数组，自动机就是在这个数组上运行的。这是什么意思呢？

我们从初始状态开始。从输入中取出第一个字符，并找到一个以该字符为标签的转换。我们跟随这个转换，将当前状态更改为最后一个字符对应的状态（这可能是同一个状态）。然后取出另一个字符并执行相同的操作。重复，直到输入结束。（我有没有提到它必须是有限长度？嗯，必须如此。）

结果可能如下：

• 我们最终进入了接受状态之一。很好。这意味着自动机接受了输入。
• 我们最终处于某种非接受状态。这意味着我们的自动机不接受输入。
• 在某些时候，我们没有找到并转换当前正在处理的字符。这并非例外——只是意味着输入未被接受。显然，如果输入包含任何非自动机所基于字母表中的字符，它将不会被接受。

使用正则表达式，我们采用它们的定义（例如/abc/），然后构建一个自动机并通过它运行一个字符串。

示例

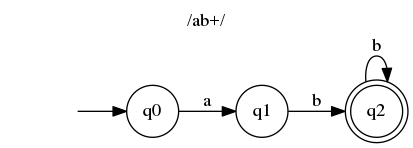
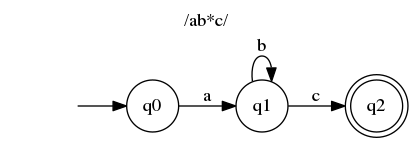
让我们看一些正则表达式的有限自动机。

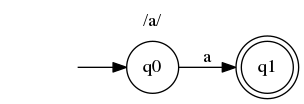
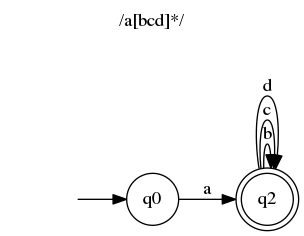
在这个非常简单的例子中，我们从 状态开始q0。如果我们的输入是"a"，我们可以通过唯一的转换过渡到q1。输入被消费，我们处于接受状态（用双圆圈表示），因此字符串与正则表达式匹配。

请注意，对于字符串"aa"，在处理完第一个字符后，我们仍然需要a处理一个字符。但是没有从 传出的转换q1，因此我们无法接受该字符串。这可能与你从编程中学到的知识相悖，但实际上/a/正则表达式实际上是/\Aa\z/。我们将在本文的其余部分以这种方式处理它们。

同时，让我们看更多的例子。

厄普西隆转变

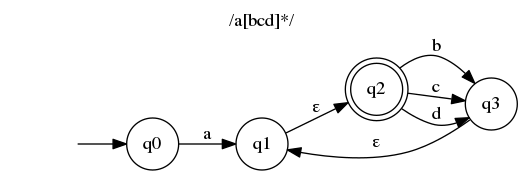
最后一个例子稍微复杂一些，引入了我们之前没有讨论过的东西：epsilon 转换。这是一种便捷的机制，可以让你的图/自动机更简单、更容易推理。它们是什么？

Epsilon 转换无需消耗任何输入字符。因此，如果我们处于q1，就可以转到q2“免费”状态。

听起来很蠢？嗯，对我来说确实如此。这意味着a在上一个例子中 ( /a[bcd]*/) 消费之后，我们都处于状态q1和q2²。幸运的是，有一个简单的算法可以消除 epsilon 转换。它创建的自动机更“精确”，但不太美观，也更难读。通常，使用 epsilon 转换从正则表达式构建一些自动机也更容易。

这是一个没有 epsilon 转换的等效自动机：

我不会详细讨论该算法，但其核心思想是：

对于每个转换，当它指向 epsilon 转换的起始状态时，用指向 epsilon 转换目标状态的转换替换它。然后移除 epsilon 转换。重复此操作，直到没有 epsilon 转换剩余。然后，修剪孤立的状态（没有输入或输出转换）。

有时它会比这更难一些，但我们不会在这里使用很多 epsilon 转换，所以我们不需要专注于此。

是否确定？

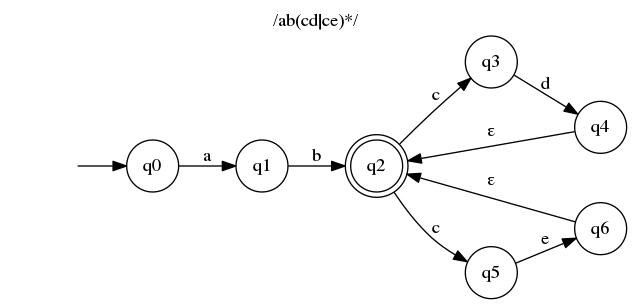
到目前为止，我们的自动机相当简单。你可能已经想过一两次如何实现它们了。然而，我们还没有讲到正则表达式中一个非常重要的部分——交替。考虑一个正则表达式：/ab(cd|ce)*/。当然，这可以用更巧妙的方式写出来（/ab(c[de])*/），但我们也没有太多选择。这个正则表达式是有效的，所以我们必须为它创建一个自动机：

当我们处于状态q2并且c输入为 时，问题就出现了。我们应该转到q3还是q5？作为人类，我们可以向前看，看得很清楚，但自动机却没有这种奢侈。我们总是需要在消费一个字符的那一刻改变状态。所以在实现中，我们需要同时处于多个状态。虽然这还不算太糟，但实际上，对于更大的自动机来说，这可能会有点慢。我们能做得更好吗？

举个例子：我们的自动机是非确定性的。它的定义是，它不是确定性自动机（.___.）。那么后者是什么呢？摘自维基百科：

• 它的每个转换都由其源状态和输入符号唯一确定，并且
• 每次状态转换都需要读取输入符号

所以，我们不能有 epsilon 转换，并且对于每个状态，只能有一个具有给定标签的转换。简单。我们就这么做吧。

NFA的确定性

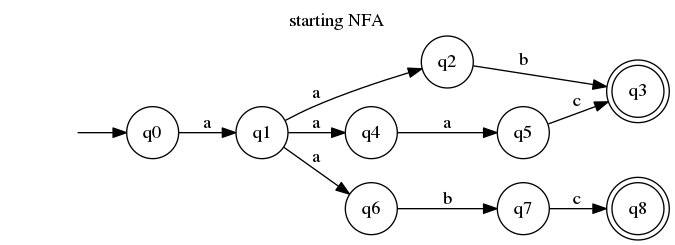
为了解释的目的，我将确定以下自动机：

你可能立刻就注意到了，问题出现在我们处于q1状态 并且a输入中有一个字符的时候。我们要转换到哪个状态呢？嗯，根据非确定性自动机的非正式定义，我们同时处于三种状态：q2，q4和q6。

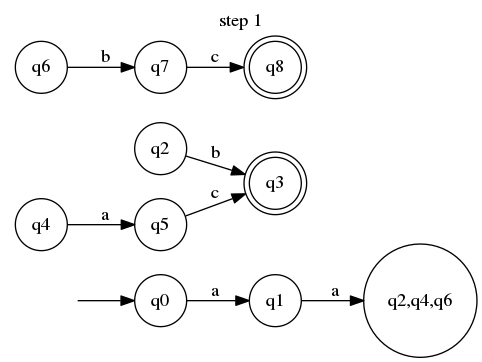
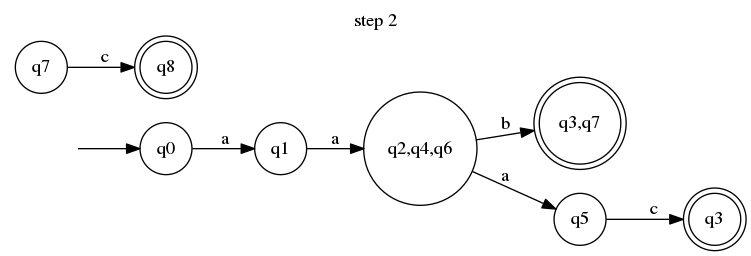
确定化过程利用了该定义，并通过创建一个表示该状态的新状态来使其显而易见。为了方便起见，我们将其称为。我们创建一个从到新状态的q2,q4,q6转换，通过，并删除所有其他源自 的带 标记的转换。这是我们的自动机在第一步之后的样子：q1aaq1

如你所见，它现在有点问题。我们需要处理那些分离的部分，从q2、q6和开始q4。这时我们的命名约定就派上用场了。从 开始q2，我们将获取它的所有转换，并将它们附加到所有“设置状态”，其中包括（在本例中，它是我们新的大状态）。我们通过 来q2创建到 的转换。q3b

然后，我们对其余的分离状态执行此操作。q4我们可以从 到达q5via b，因此现在我们创建一个从q2,q4,q6到q5via 的转换b。对于q6– via ，b我们可以到达q7，但我们已经有一个标记为b(to ) 的转换。为了解决此冲突，我们创建另一个“设置状态” ，q3而不是。q3q3,q7

另一件重要的事情是：q3存在一个接受状态。我们新创建的q3,q7状态也应该是接受状态。这也来自 NFA 的非正式定义：如果我们处于多个状态，但至少其中一个是接受状态，则自动机将接受迄今为止消耗的输入。

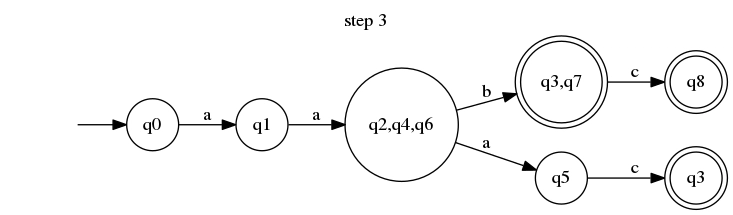
只剩下一个分离状态，我们必须重复上一步所做的事情：获取它，找到包含的所有“设置状态” q7（在本例中只有q3,q7）并重写转换。

现在，我们可以享受到与最初的非确定性自动机等价的确定性版本了。它变得简单了一些（状态从 9 个变成了 7 个，转换从 9 个变成了 6 个）。通过将其逆向工程为正则表达式，我们也能得到一个更简单的版本！NFA 的正则表达式为 ，/a(ab|aac|abc)/而我们的 DFA 的正则表达式为/aa(bc?|ac)/。

但这并不总是那么明显，有时确定性自动机比非确定性自动机更复杂。

完全自动机

如果你了解自动机理论，尤其是数学家，你现在可能正怒不可遏，差点翻到评论区告诉我，上面的代码不是确定性有限自动机。其实你是对的。我漏掉了一点，但你很快就会明白为什么。

确定性自动机的正式定义要求它是完备的。这是什么意思呢？对于字母表中的每个状态和每个字符，都应该有一个从该状态发起并由该字符标记的转换。这意味着我们需要大量的转换，但作为额外的好处，我们永远不会陷入这样的境地：虽然我们还没有处理完所有输入，但却因为没有匹配的转换而无法继续。

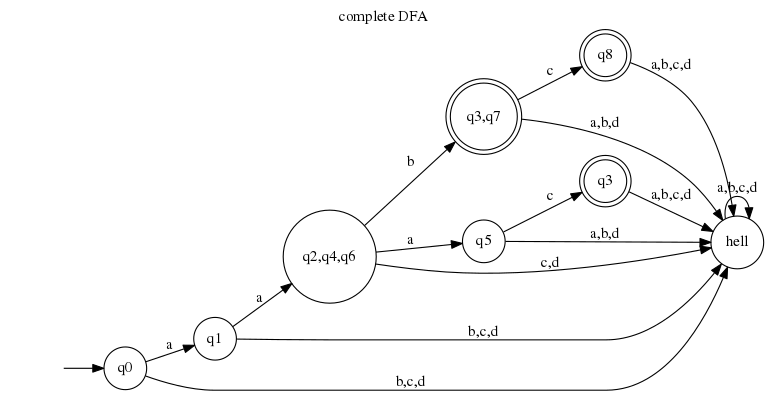
这是通过引入一个额外的状态来实现的。我们以前称之为“地狱”。有了它，假设我们的字母表很简单{a,b,c,d}，我们就可以使我们的DFA完整。像这样：

所以，现在它读起来不太好，即使我画得简洁。然而，在编程中使用正则表达式时，我们通常希望字母表包含所有 Unicode 字符。而且 Unicode 字符有很多，真的很多。这就是为什么我们通常不想创建完全自动机。

我们在这里

目前基本就是这样。确定性自动机是正则表达式编译的结果。现在我们可以把一些字符串输入进去，它会判断是否接受。我原本计划放一个示例实现，但这篇文章已经很长了，所以我会把它安排在第二部分。最后，关于目前为止我们所做的一些说明：

• 我们现在知道如何构建正则表达式的自动机，它由一些基本特征组成，例如，，，，。*我没有讲到它，但也可以有，，以及。+()|{n}{n,}{n,m}?
• 我们不知道如何处理范围和组。此外，我们不知道如何处理点号（匹配任意字符）。这些其实都是实现细节，从理论角度来看并不重要。尤其是当我们想让点号匹配任意 Unicode 字符时，需要一些技巧，但我们现在先不讨论。
• 我们不能使用反向引用、前瞻或类似的功能。即使更强大的功能，我们也用不了，因为不可能创建有限自动机来处理它们。你需要不同的理论设备（我认为是带堆栈的自动机），但那是完全不同的故事……
• 上面所有的例子实际上都是/\Aabc\z/，而不仅仅是/abc/。你必须创建一个包含所有子字符串的集合来运行自动机，并检查其中是否有匹配项。这虽然不方便，但这也是为什么你应该尽可能使用 和 的原因，因为\A它\z会更快。
• 与仅仅针对输入运行自动机相比，创建自动机并随后对其进行确定性计算的成本很高。如果您不确定您的语言是否会对其进行内部优化，则应始终在任何循环之外编译正则表达式。这是一种即时且免费的优化。现在您知道原因了。
• 另外，如果你正在编写一些性能至关重要的代码，那么你应该首先考虑使用正则表达式以外的其他方法。检查一个字符串是否是另一个字符串的子字符串比使用正则表达式检查要快得多。所以if user_agent =~ /Explorer/从现在开始就不用了，好吗？

脚注

1. “Regex” 和 “regexp” 在网上似乎可以互换使用。我自己更喜欢后者，也会用它，但它们其实是一回事 。↩

2. 我认为它们是为了帮助解决自动机串联的数学证明而引入的。不过我对此并不确定 。↩