理解时间复杂度 - 大 O 符号

最近，我对算法产生了兴趣，我首先选择深入研究的是排序算法的工作原理及其时间复杂度。然而，这篇文章并非旨在解释排序算法，而是退一步，用尽可能简单的方式理解时间复杂度（大O符号）。

在进一步讨论之前，让我们先了解一下什么是算法：

算法是一条逐步指令，指示程序以特定方式执行以解决特定问题。显而易见，当我们用任何语言运行程序时，它都会有自己的执行时间，具体取决于各种因素，例如输入、正在执行的操作等。

现在下一个问题是“时间复杂度是什么”？

时间复杂度是指算法解决问题所需的执行时间。很简单，对吧？

进一步解释一下，时间复杂度由两个因素决定，即执行时间和程序所需的空间。

为什么需要衡量时间复杂度？

作为程序员，在编写程序时，理解我们正在执行的各种操作非常重要，这可以通过测量复杂度来检查。通常，执行时间是理所当然的，我们并不关心幕后发生的微小计算。因此，总的来说，时间复杂度有助于我们提高代码的效率。

我们如何衡量时间复杂度？

当字母 O 表示时，答案是大 O 符号Order of the program。

大 O 符号（一种数学表达式）通过对程序在不同输入和不同操作下的行为进行分类来帮助测量时间复杂度。

让我们了解常见的符号类型，这里我们将使用 Javascript 来举例说明，尽管不同语言的想法是相似的。

大 O 符号的类型：

• 恒定时间算法 - O(1) - 阶数 1：这是最快的时间复杂度算法，因为执行程序所需的时间总是相同的。无论输入的大小如何，执行过程和运行所需的空间都是相同的。例如：以简单的数组查找或获取数组的最后一项为例。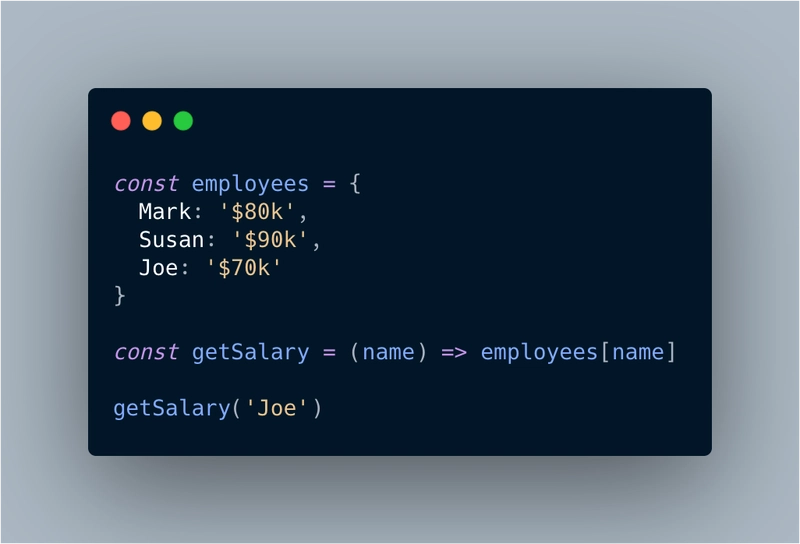上面的例子总是会遍历数组一次，并找到名为 的员工的工资Joe。这意味着，它涉及恒定（固定）迭代，即O(1)。
• 线性时间算法 - O(n) - N 阶：线性时间复杂度完全取决于输入大小，即成正比。其中一个例子可能是仅打印数组中的元素或在数组中查找特定匹配项。在计算时，我们应该始终考虑“最佳”和“最差”情况。例如：如果我们要匹配数组中的特定元素，那么它可以是第一个元素，也可以是最后一个元素，因此在这种情况下，我们可以假设它的复杂度为 O(n)。让我们在这里举个例子：
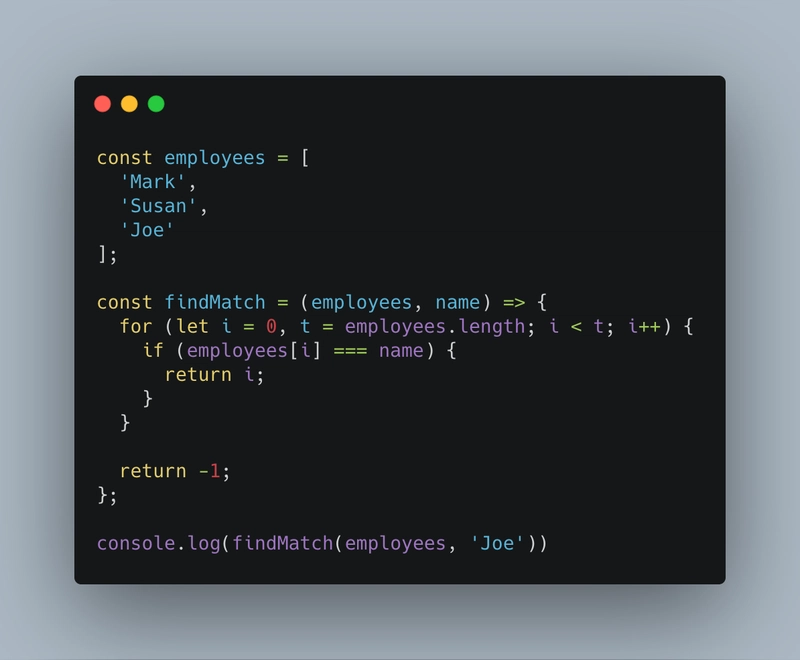
• 二次时间复杂度 - O（n2）- N 阶平方：顾名思义，执行程序的时间与输入大小的平方成正比。这意味着，在我们的程序中，当我们尝试执行两种兼具线性和恒定时间复杂度的操作时，这些操作称为二次时间复杂度。这种复杂度通常用于排序算法。让我们通过一个例子来理解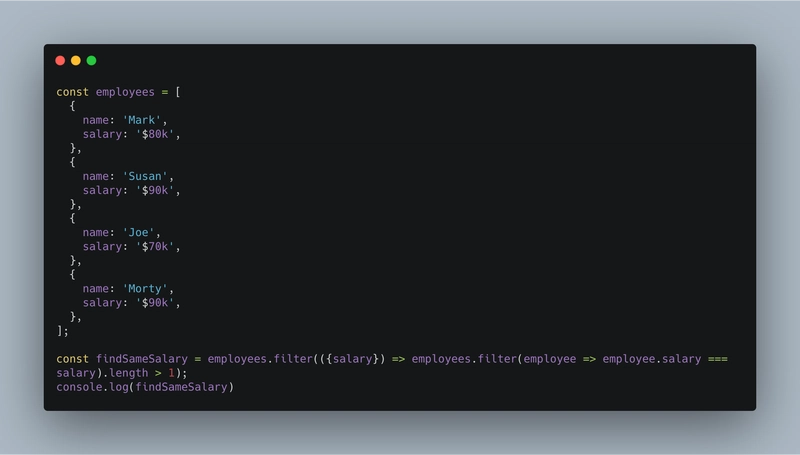：在这个例子中，很明显我们首先在顶部有一个单独的过滤循环，它对一个数组进行一次迭代，然后我们有一个嵌套循环，通过再次迭代该数组来查找员工的相似工资。
• 对数时间算法 - O（log n） - 顺序 log N：这被认为是处理集合中大量数据的最有效方法。这种方法背后的想法是将数据分成块，然后执行操作。Alogarithm基本上是一个代表基数幂的量，这意味着如果数据呈对数增长，那么它实际上就是被除数。例如，如果我们想从 50 条记录中找到几个员工的工资，那么这意味着我们通常必须浏览每条记录并寻找它。假设如果我们使用log base 2，我们将能够在log2(50) = ~6迭代中找到它。那是多么强大的力量！它通常与不同的排序算法一起使用，例如快速排序、合并排序，通常用于查找元素或对列表进行排序。或者二进制搜索就是一个很好的例子。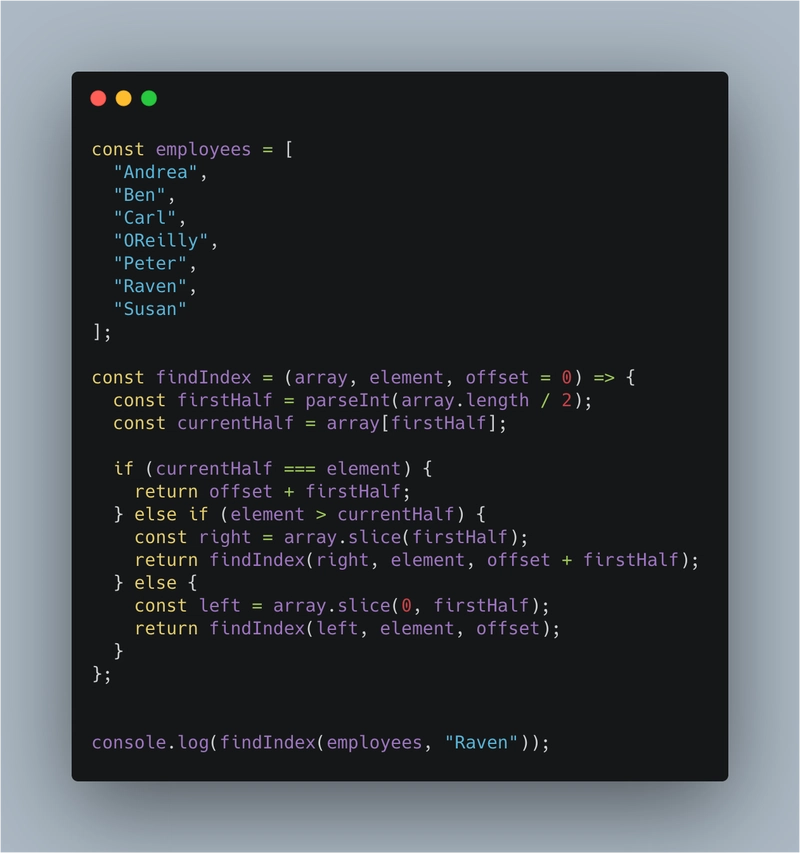

我想我们已经涵盖了最常用的符号。如果你想了解更多，我推荐以下几个不错的链接：

• Big O 备忘单
• 初学者指南

谢谢阅读。😃
访问我的博客查看原文。