动态规划与分治法

或采用分而治之的策略

或采用分而治之的策略

TL;DR

在本文中，我尝试通过两个示例来解释动态规划和分治方法之间的差异/相似之处：二分搜索和最小编辑距离（Levenshtein 距离）。

问题

当我开始学习算法时，我很难理解动态规划（DP）的主要思想以及它与分治（DC）方法的区别。当比较这两个范式时，通常斐波那契函数是一个很好的例子。但是，当我们尝试使用DP和DC方法分别解释它们来解决同一个问题时，我感觉我们可能会丢失一些有价值的细节，而这些细节可能有助于更快地捕捉到它们之间的差异。而这些细节告诉我们，每种技术最适合解决不同类型的问题。

我仍在理解动态规划和分治法的区别，目前还不能说我已经完全掌握了这些概念。但我希望本文能提供一些额外的启发，并帮助你更进一步地学习动态规划和分治法等有价值的算法范式。

动态规划与分治法的相似之处

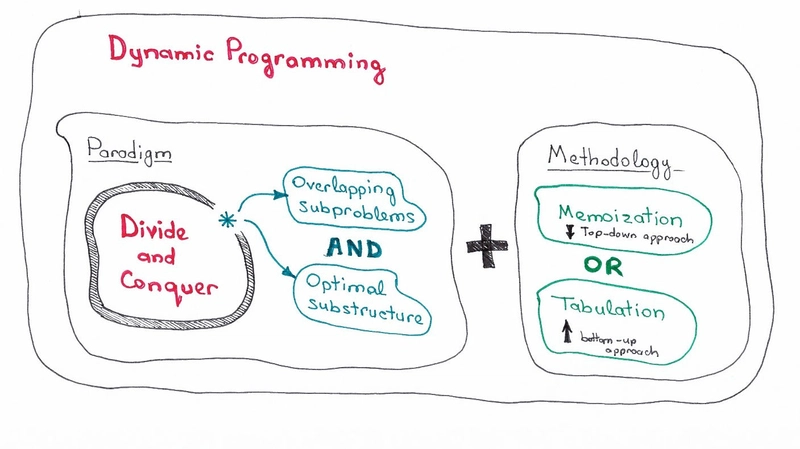
据我目前所见，我可以说动态规划是分而治之范式的延伸。

我不会把它们视为完全不同的东西。因为它们 都是通过递归的方式将一个问题分解成两个或多个相同或相关类型的子问题，直到它们变得足够简单，可以直接求解。然后将子问题的解组合起来，得到原始问题的解。

那么，为什么我们仍然有不同的范式名称，以及为什么我将动态规划称为扩展。这是因为只有当问题具有某些 限制或先决条件时，动态规划方法才可能被应用。并且，动态规划通过记忆化或制表技术扩展了分治法。

让我们一步一步来……

动态规划先决条件/限制

正如我们刚刚发现的，为了使动态规划适用，分治问题必须具备两个关键属性：

1. 最优子结构 ——最优解可以通过其子问题的最优解构建
2. 重叠子问题 ——问题可以分解为可重复使用的子问题，或者问题的递归算法可以反复解决相同的子问题，而不是总是生成新的子问题

一旦满足这两个条件，我们就可以说这个分而治之的问题可以用动态规划方法来解决。

分而治之的动态规划扩展

动态规划方法通过两种技术（记忆化和制表）扩展了分治法，这两种技术都旨在存储和重用子问题的解决方案，从而显著提升性能。例如，斐波那契函数的简单递归实现的时间复杂度为 ，而O(2^n)动态规划解决方案只需花费时间即可完成相同的操作O(n)。

记忆化（自上而下的缓存填充）是指缓存并重用先前计算结果的技术。fib因此，记忆化函数如下所示：

memFib(n) {
    if (mem[n] is undefined)
        if (n < 2) result = n
        else result = memFib(n-2) + memFib(n-1)
        mem[n] = result
    return mem[n]
}

制表法（自下而上的缓存填充）与之类似，但侧重于填充缓存条目。计算缓存中的值最简单的方法是迭代完成。制表法fib如下所示：

tabFib(n) {
    mem[0] = 0
    mem[1] = 1
    for i = 2...n
        mem[i] = mem[i-2] + mem[i-1]
    return mem[n]
}

您可以在此处阅读有关记忆和制表比较的更多信息。

您应该在这里掌握的主要思想是，由于我们的分而治之问题具有重叠的子问题，因此子问题解决方案的缓存成为可能，因此记忆/制表便应运而生。

那么 DP 和 DC 到底有什么区别呢？

由于我们现在已经熟悉了 DP 先决条件及其方法，我们准备将上面提到的所有内容放在一幅图中。

让我们尝试使用 DP 和 DC 方法解决一些问题，以使这个例子更清晰。

分治法示例：二分查找

二分查找算法，也称为半区间查找，是一种在已排序数组中查找目标值位置的搜索算法。二分查找会将目标值与数组的中间元素进行比较；如果它们不相等，则排除目标值无法所在的一半，并继续在剩余的一半中搜索，直到找到目标值。如果搜索结束时剩余的一半为空，则表示目标值不在数组中。

例子

这是二分搜索算法的可视化，其中4是目标值。

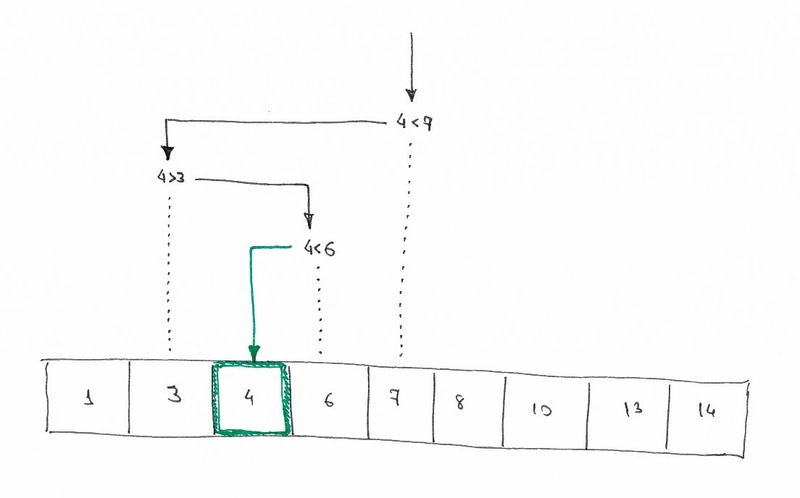
让我们以决策树的形式绘制相同的逻辑。

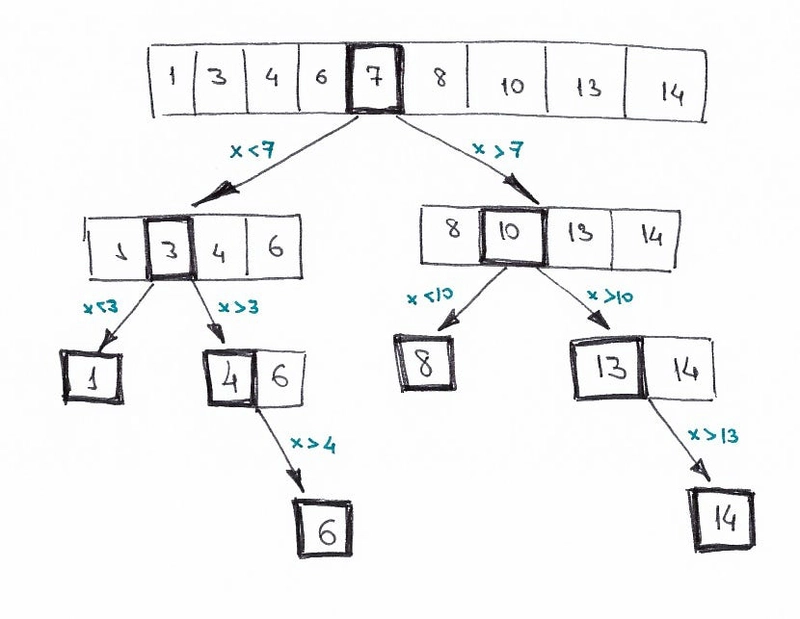
你可能清楚地看到了解决问题的分而治之原则。我们迭代地将原始数组拆分成子数组，并尝试在其中找到所需的元素。

我们可以用动态规划来解决这个问题吗？不能。这是因为不存在重叠的子问题。每次我们都会把数组拆分成完全独立的部分。而根据分治法的先决条件/限制，子问题必然会以某种方式重叠。

通常，每次你画一棵决策树，它实际上是一棵树（而不是决策图），这意味着你没有重叠的子问题，这不是动态规划问题。

代码

在这里您可以找到二分搜索函数的完整源代码以及测试用例和解释。

函数 binarySearch(sortedArray，seekElement) {
  让 startIndex = 0;
  让 endIndex = sortedArray.length - 1;

  while (startIndex <= endIndex) { 
    const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2);

    // 如果我们找到了该元素，则返回其位置。
    if (sortedArray[middleIndex] === seekElement)) { 
      return middleIndex; 
    }

    // 决定选择哪一半：左半还是右半。
    if (sortedArray[middleIndex] < seekElement)) { 
      // 转到数组的右半部分。
      startIndex = middleIndex + 1; 
    } else { 
      // 转到数组的左半部分。
      endIndex = middleIndex - 1; 
    } 
  }

  返回 -1; 
}

动态规划示例：最小编辑距离

通常，在动态规划示例中，斐波那契数列算法是默认采用的。但让我们采用一个稍微复杂一点的算法，以便我们能够理解其中的概念。

最小编辑距离（或 Levenshtein 距离）是衡量两个序列之间差异的字符串指标。通俗地说，两个单词之间的 Levenshtein 距离是指将一个单词更改为另一个单词所需的最小单字符编辑（插入、删除或替换）次数。

例子

例如 ，“kitten”和“sitting”之间的Levenshtein距离为3，因为接下来的三次编辑会将一个单词改变为另一个单词，而没有办法用少于三次的编辑来完成这一改变：

1. k itten → s itten （用 “s” 代替 “k”）
2. sitt e n → sitt i n（用“i”替换“e”）
3. sittin → sittin g（在末尾插入“g”）。

应用

它有广泛的应用，例如拼写检查器、光学字符识别的校正系统、模糊字符串搜索以及基于翻译记忆辅助自然语言翻译的软件。

数学定义

a从数学上讲，两个字符串（b长度分别为|a|和）之间的编辑距离|b|由函数给出，lev(|a|, |b|)其中

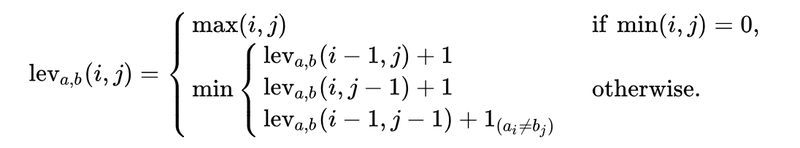
请注意，最小值中的第一个元素对应于删除（从a到b），第二个元素对应于插入，第三个元素对应于匹配 或不匹配，具体取决于相应的符号是否相同。

解释

好的，让我们试着弄清楚这个公式的含义。我们举一个简单的例子，求字符串ME和MY之间的最小编辑距离。直观地看，你已经知道这里的最小编辑距离是1 个操作，这个操作是“用Y替换E ”。但为了能够处理更复杂的例子，比如将Saturday替换为Sunday ，我们尝试将其形式化为算法形式。

要将公式应用于M E →M Y变换，我们需要事先知道ME→M、M→MY和M→M变换的最小编辑距离。然后，我们需要选取最小的一个，并添加 +1 运算，将最后一个字母E→Y进行变换。

因此，我们已经可以看到该解决方案的递归性质：ME→MY变换的最小编辑距离是基于三个先前可能的变换来计算的。因此，我们可以说这是一种分而治之的算法。

为了进一步解释这一点，我们绘制以下矩阵。

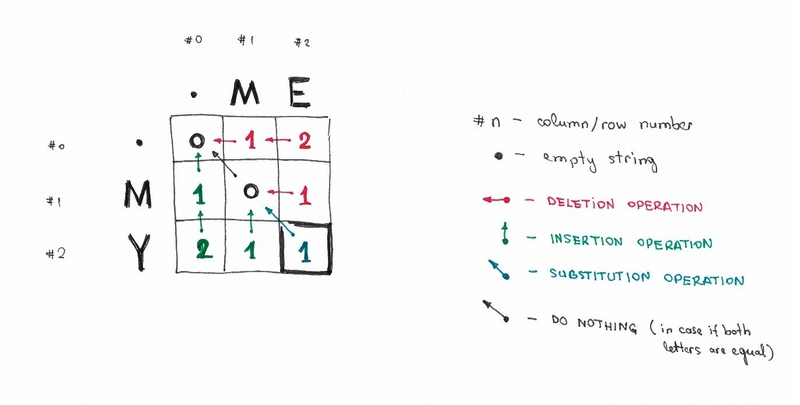
单元格 (0,1)包含红色数字 1。这意味着我们需要执行 1 次操作才能将M转换为空字符串：删除M。这就是为什么这个数字是红色的原因。

单元格 (0,2)包含红色数字 2。这意味着我们需要 2 个操作将ME转换为空字符串：删除E，删除M。

单元格 (1,0)包含绿色数字 1。这意味着我们需要 1 个操作将空字符串转换为M：插入M。这就是这个数字显示为绿色的原因。

单元格 (2,0)包含绿色数字 2。这意味着我们需要 2 个操作将空字符串转换为MY ：插入Y，插入M。

单元格 (1,1)包含数字 0。这意味着将M转换为M不需要任何成本。

单元格 (1,2)包含红色数字 1。这意味着我们需要 1 个操作将ME转换为M：删除E。

等等…

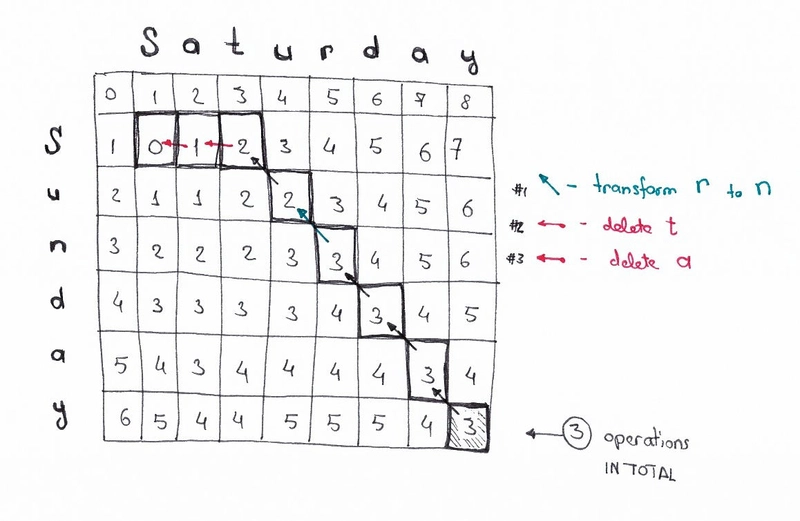
对于像我们这样的小矩阵（只有 3x3），这看起来很容易。但是对于更大的矩阵（比如 9x7 矩阵，用于周六→周日的转换），我们如何计算所有这些数字呢？

好消息是，根据公式，你只需要三个相邻的单元格(i-1,j)、(i-1,j-1)和(i,j-1)来计算当前单元格 的数字(i,j) 。我们需要做的就是找到这三个单元格中的最小值，然后如果i-s行和j-s列的字母不同，则加1。

因此，您可能再次清楚地看到问题的递归性质。

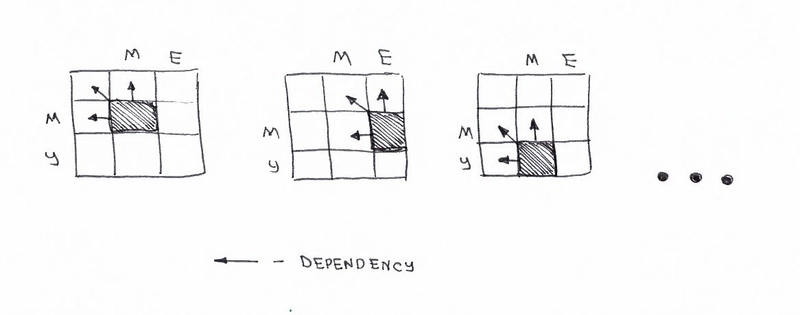
好的，我们刚刚发现我们处理的是分而治之的问题。但是我们可以应用动态规划方法来解决这个问题吗？这个问题是否满足我们的重叠子问题和最优子结构限制？是的。让我们从决策图中看看。

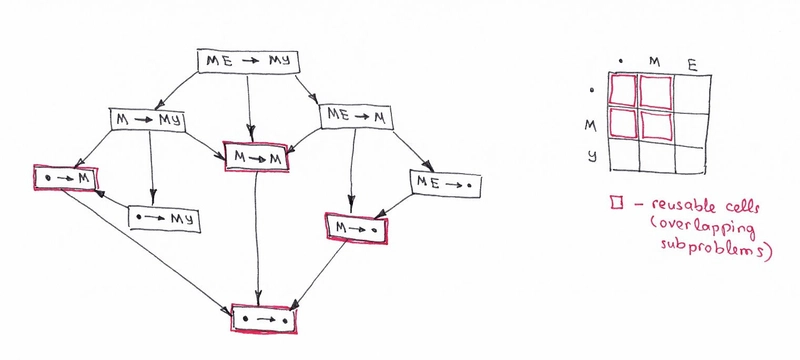
首先，这不是决策树。这是一个决策图。您可能会在图片上看到许多重叠的子问题，并用红色标记。此外，没有办法减少运算次数，使其小于公式中三个相邻单元格的最小值。

您可能还会注意到，矩阵中每个单元格的编号都是根据之前的单元格编号计算的。因此，这里应用了制表技术（自下而上填充缓存）。您将在下面的代码示例中看到它。

进一步应用这个原则，我们可以解决更复杂的情况，比如星期六→星期日的转换。

代码

在这里您可以找到最小编辑距离函数的完整源代码以及测试用例和解释。

函数 levenshteinDistance(a，b) { 
  const distanceMatrix = Array(b.length + 1) 
    .fill(null) 
    .map( 
      () => Array(a.length + 1).fill(null) 
    );

  对于（让 i = 0; i <= a.length; i += 1）{
    距离矩阵[0][i] = i; 
  }

  对于（让 j = 0; j <= b.length; j += 1）{
    距离矩阵[j][0] = j; 
  }

  for (let j = 1; j <= b.length; j += 1) { 
    for (let i = 1; i <= a.length; i += 1) { 
      const indicator = a[i - 1] === b[j - 1] ? 0 : 1; 
      
      distanceMatrix[j][i] = Math.min( 
        distanceMatrix[j][i - 1] + 1, // 删除
        distanceMatrix[j - 1][i] + 1, // 插入
        distanceMatrix[j - 1][i - 1] + indicator, // 替换
      ); 
    } 
  }

  返回距离矩阵[b.长度][a.长度]; 
}

结论

在本文中，我们比较了两种算法方法，即动态规划和分治法。我们发现，动态规划基于分治原则，并且仅适用于问题存在重叠子问题且存在最优子结构的情况（例如编辑距离的情况）。动态规划则使用记忆或制表技术来存储重叠子问题的解以供后续使用。

我希望这篇文章不会给您带来更多困惑，而是能让您了解这两个重要的算法概念！:)

您可以在JavaScript 算法和数据结构存储库中找到更多分而治之和动态规划问题的示例，其中包含解释、注释和测试用例。

编码愉快！