后端开发教程 - Java、Spring Boot 实战 - msg200.com
Big-O 符号：初学者指南
大 O 符号
总结
更多资源
在编程的世界里，把今天当作生命中的最后一天来写代码，这在编程艺术中并非最重要的。除了理解我们的代码要解决的问题之外，我们在编写代码时还需要考虑其他变量。例如：
- 复杂
- 可维护性
- 设计模式
- 算法
- 以及更多……
本文最重要的事情之一和主题是我们在实现算法时应用程序的性能。
我们算法的卓越性能有助于我们提升应用程序的用户友好度，让用户只需投入必要的时间完成任务，并在感到无聊并关闭窗口（浏览器或其他任何程序）之前专注于其他任务。无论用户使用的设备速度有多快、操作有多熟练，都能确保应用程序的流畅运行。在当今世界，时间是我们最宝贵的财富。
当我们谈论性能时，需要考虑许多变量，例如内存使用、磁盘空间、执行时间等等。
确定算法性能的最重要工具之一是大 O 符号。
大 O 符号
大 O 符号是一种工具，可以让我们确定算法的复杂度，从而衡量特定算法的性能。该工具可以测量算法达到需求最高点的最坏情况。
Big-O 的主要术语如下：
- O(1) ->常数
- O(n) ->线性
- O(log n) ->对数
- O(n ^ 2) ->二次
- O(2 ^ n) ->指数
O(1)：常数复杂度
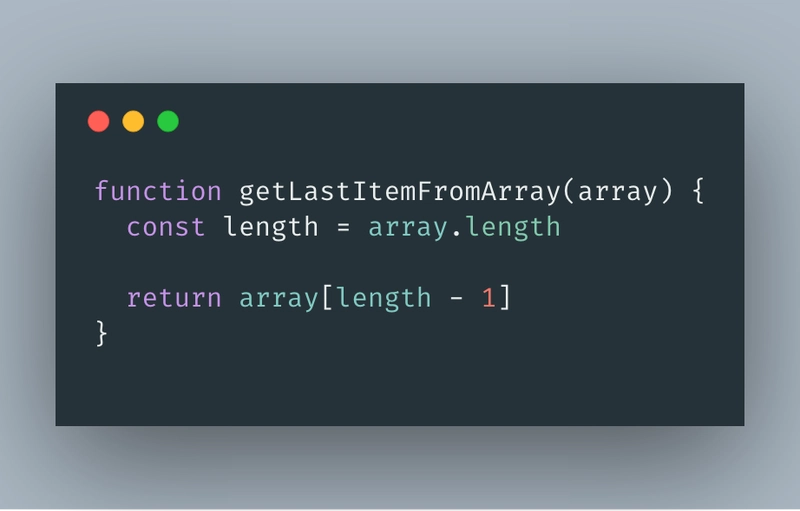
常数复杂度更容易理解，所有算法，无论输入或输出的大小、执行时间和所用资源始终相同，都具有这种复杂度。无论算法执行多少次或在哪里执行，它的行为始终完全相同。例如：
如我们所见，无论参数传入的数组大小如何，其行为始终保持不变。唯一可能改变的是输出，因为数组中存储的数据可能并非始终相同。
O（n）：线性复杂度
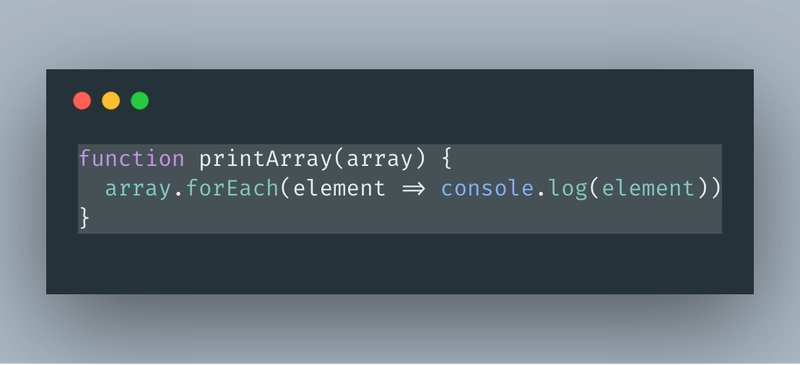
当一个算法的执行时间和/或所用资源与输入大小成正比（线性增长）时，我们称该算法具有线性复杂度。例如：
为了更容易理解这种复杂性，我们可以将其与我们每天（或大部分时间）进行的活动进行比较，例如读书或看电影。我们花在阅读一本书或看电影上的时间取决于书的页数和电影的时长。例如，如果一部电影的时长为两个小时，那么您将花两个小时看完一部电影。如果这本书有一百页，而您在一小时内阅读了五十页，那么您将花两个小时阅读整本书。
O（log n）：对数复杂度
这种复杂性体现在算法的影响与输入大小的对数结果成正比。换句话说，当输入大小为 10 时，我们需要 1 秒的时间用算法完成任务，那么当输入大小为 100 时，我们需要在 2 秒内完成完全相同的任务，当输入大小为 1000 时，我们需要在 3 秒内完成完全相同的任务，以此类推。
一个有趣的例子是二分查找。在这个算法中，我们将数组（先前排序）分成两部分。我们以中间索引为参考，以获取数组中间的值。如果该位置的数字等于我们要查找的数字，则返回中间索引加上我们用来查找存储我们要查找的数字的位置的前缀。因此，如果数字大于存储在数组中间的数字，则我们在数组的右侧寻找数字，如果小于，则在数组的左侧寻找。之后，我们以递归的方式使用该前缀作为下一次迭代中的新前缀。我们重复此循环，直到获得给定的数字。
O(n^2)：二次复杂度
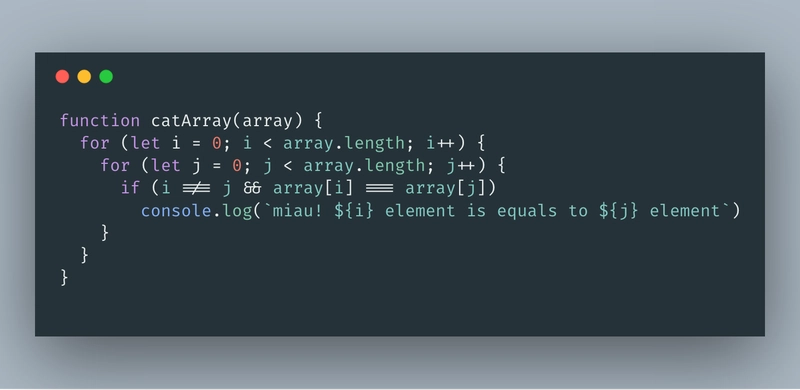
当算法的影响与输入大小的平方成正比时，就会出现二次复杂度。这意味着，如果我们有一个长度为 4 个点的数组作为输入，并且我们想要比较数组中是否有重复项，那么我们需要进行 16 次比较才能完成任务。这种复杂度在冒泡排序、插入排序和选择排序等排序算法中很常见。
在这个函数中，如果我们添加更多的 for 循环，复杂度就会增加。这可能会使复杂度达到 O(n * n)。
O(2^n)：指数复杂度
当一个算法具有指数复杂度时，这意味着输入中每增加一个项，复杂度就会翻倍。如果处理 10 个项需要 100 秒，那么处理 11 个项则需要 200 秒，处理 13 个项则需要 400 秒，以此类推。
这并不意味着只能存在 O( 2^n )，这只是为了解释。它可以扩展到 O( 3^n )、O( 4^n ) 等等。
总结
我希望这能帮助您更好地理解 Big-O 符号，它对于衡量算法的复杂性有很大帮助，还有许多其他工具可以做到这一点，但这是最常见的工具之一。
如果您有任何疑问或想纠正一些错误，请随时在下方留言。我在下面列出了一些关于大 O 符号的资源。
更多资源
-
https://rob-bell.net/2009/06/a-beginners-guide-to-big-o-notation/
-
http://interactivepython.org/runestone/static/pythonds/AlgorithmAnalysis/BigONotation.html