使用 Big-O 的数组优势、劣势、插入和删除算法
数组是计算机科学和编程中的基本数据结构,具有一系列影响其效率和可用性的优势、劣势和 Big-O 复杂性。
了解数组的特性对于为特定任务选择正确的数据结构和优化程序性能至关重要。
在本文中,我们将深入探讨数组的优势、劣势以及 Big-O 复杂度。我们探索了数组的优势,例如随机和顺序访问、实现简单以及缓存友好性。同时,我们也讨论了数组的局限性,包括固定大小、插入和删除操作的挑战以及缺乏灵活性。
此外,我们还讨论了常见数组操作(例如访问、查找、插入、删除和调整大小)的时间复杂度。通过深入了解这些方面,程序员可以在使用数组时做出明智的决策,并在应用程序中有效地平衡效率和功能。
优势
使用数组有很多优点,其中一些概述如下:
- 快速查找(随机访问)
- 快速附加
- 简单实现
- 缓存友好性
1.快速查找(随机访问)
无论数组的长度如何,检索给定索引处的元素都需要 O(1) 时间。
例如:
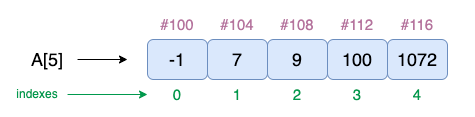
int[] A = {-1, 7, 9, 100, 1072};
该数组有五个元素,数组的长度使用 计算,A.length即。由于数组是从零索引的,因此5使用 访问最后一个元素,如下图所示。A[A.length - 1]A[4]
如果我们使用索引访问数组元素,例如A[0]或A[4],则需要一个单位的时间,或者用大 O 术语来说,需要一个常量操作。
A[0]; // -1
A[3]; // 100
A[4]; // 1072
A[5]; // Index out of bounds exception, as there is no A[5] value.
所有上述操作都消耗一个时间单位,即 O(1) 时间。
2. 快速附加
O(1)如果数组有空间,则在数组末尾添加新元素需要时间。
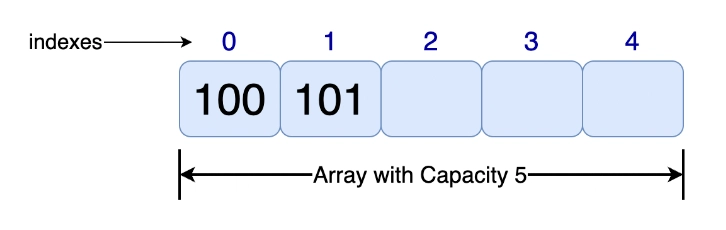
让我们创建一个具有容量的数组,并在索引和处5插入值和。10010101
下面的代码解释了这一点。
int[] A = new int[5];
A[0] = 100;
A[1] = 101;
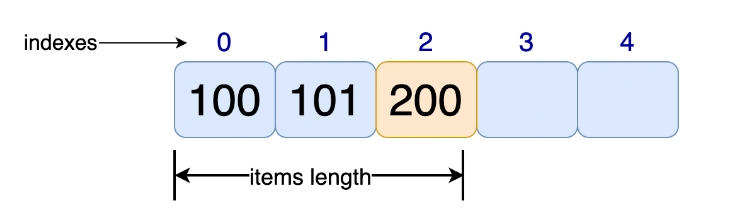
现在,如果我们要向数组中插入一个新值,我们可以这样做A[2] = 200。这会将值插入200到索引处2。此操作消耗一个单位时间,该时间是恒定的。
这就是末尾附加速度很快的原因。
废话不多说。这里有一个简单的算法,创建一个大小为 的数组5,并向其中插入 个值。最后,我们在数组长度处插入一个元素100。101
import java.util.Arrays;
public class ArrayAppends {
public static void main(String[] args) {
int[] A = new int[5];
int currentLength = 0;
// Let us add 2 elements to the array
for (int i = 0; i < 2; i++) {
A[i] = i + 100;
currentLength++; // when i=1, length is set to 2
}
System.out.println(Arrays.toString(A)); // [100, 101, 0, 0, 0]
System.out.println("current array items length " + currentLength); // 2
System.out.println("Array capacity " + A.length); // 5
System.out.println(
"Element insert at end "
+ Arrays.toString(insertAtEnd(A, currentLength))); // [100, 101, 200, 0, 0]
}
// Inserting element at the end
public static int[] insertAtEnd(int[] A, int currentLength) {
A[currentLength] = 200;
return A;
}
}
/*
Outputs:
[100, 101, 0, 0, 0]
current array items length 2
Array capacity 5
Element insert at end [100, 101, 200, 0, 0]
*/
3.简单实现
在大多数编程语言中,数组都有直接的实现,因此易于理解和使用。
4.缓存友好性
数组中的元素连续存储在内存中,这提高了缓存性能并可以加快访问时间。
弱点
使用数组有一些缺点,其中一些概述如下:
- 固定大小。
- 内存未使用或浪费。
- 尺寸加倍。
- 昂贵的刀片
- 昂贵的删除
1. 固定大小
数组在创建时就定义了固定的大小。添加或删除超出初始大小的元素需要创建新数组并复制现有元素,这可能效率低下。
您需要提前指定要在数组中存储多少个元素。(除非您使用高级动态数组)。
int[] A = new int[5]; // contains 5 elements
2. 内存未使用或浪费
如果数组的大小大于其包含的元素数量,则会浪费内存。
假设有一个容量为 的数组5。我们有两个元素需要存储在这个数组中,这样就浪费了三个未填充的单元格,并且浪费了内存,这意味着3*(4 bytes) = 12浪费了 byte 的内存(整数占用4byte 的空间)。
3. 尺寸加倍
假设一个数组的容量为 个5元素。但是我们想要存储的元素更多,这意味着我们必须将数组的大小加倍,创建一个新数组,复制旧数组元素并添加新元素。时间复杂度为O(n)。
您将在下一课中学习如何将数组大小加倍。
4. 昂贵的刀片
在数组末尾插入/追加元素需要O(1)时间。我们在优势(快速追加)中已经看到了这一点。
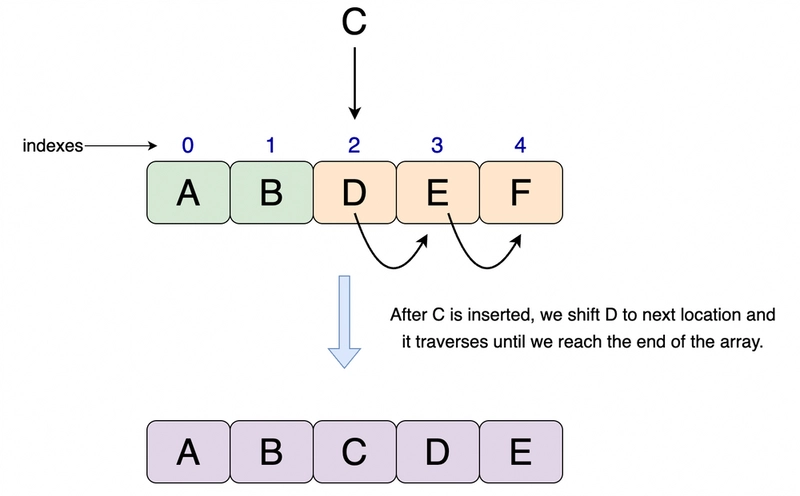
但是,在数组的开头/中间插入元素需要O(n)时间。为什么?🤔
如果我们想在数组中插入数据,首先,我们必须从插入的索引开始“略过”所有内容,腾出空间,如图所示。最坏的情况是,我们插入到数组的第 0 个索引(前置),所以我们必须“略过”所有内容。这就是O(n)时间。
在第二个索引处插入一个元素,并将其余元素右移一次。结果数组变为 – { A, B, C, D, E }。
在接下来的课程中,您将了解有关插入和移位算法的更多信息,并通过清晰的解释、代码片段和草图来理解为什么这些插入在开始和中间很昂贵。
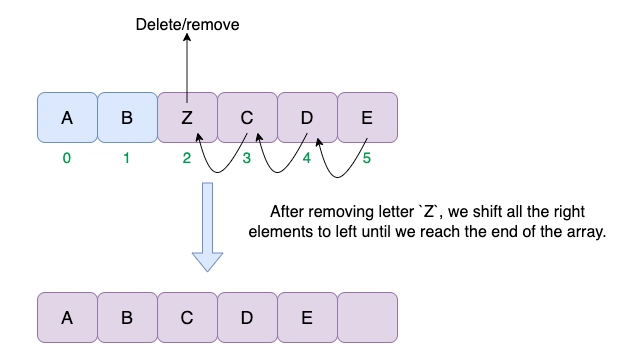
5. 昂贵的删除
删除数组末尾的元素需要O(1)时间,这是最好的情况。在计算机科学中,我们研究算法时只关心最坏的情况。但是,当我们从数组中间或开头删除一个元素时,我们必须通过快速移动它后面的所有元素来填补空缺。O(n)如果我们考虑从第 th 个索引删除一个元素的情况,就会出现这种情况0。
删除第 rd 个索引处的元素3,并通过左移其余元素来填补空白;结果数组变为 – { A, B, C, D, E }。
Big-O 复杂性
| 手术 | 复杂 | 解释 |
|---|---|---|
| 查找/访问给定索引处的值 | O(1) | 通过索引访问元素是一个恒定时间操作。 |
| 在数组中搜索元素 | 在) | 在未排序的数组中搜索特定元素在最坏的情况下需要遍历每个元素。 |
| 更新给定索引处的值 | O(1) | 更新任何给定索引处的任何元素始终是恒定时间。 |
| 在开头/中间插入 | 在) | 在数组的开头或中间插入元素需要移动现有元素,因此时间复杂度为线性。 |
| 附加到末尾 | O(1) | 如果数组有可用空间,则在末尾插入元素需要恒定的时间。 |
| 删除开头/中间部分 | 在) | 从数组的开头或中间删除一个元素需要移动剩余元素,因此时间复杂度为线性。 |
| 删除末尾 | O(1) | 删除数组的最后一个元素可以在恒定时间内完成。 |
| 调整数组大小 | 在) | 调整数组大小需要创建一个新数组并复制现有元素,这需要线性时间。 |
上面提到的 Big-O 复杂度指的是基本操作,并且假设数组为无序数组。一些专门的数据结构,例如堆或哈希表,可以为特定用例提供更高效的替代方案。
在接下来的课程中,你将学习更多关于数组容量与长度、插入和删除算法的知识。这些算法最简单,但功能最强大,可以帮助你解决数组问题。
文章来源:https://dev.to/ggorantala/array-strengths-weaknesses-and-big-o-complexity-analysis-4aho 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com