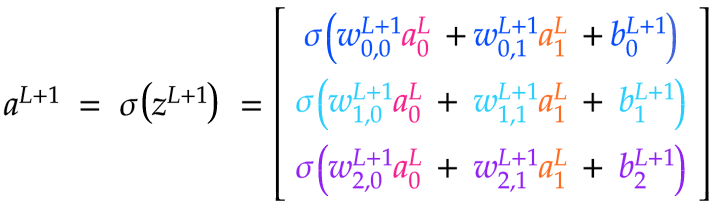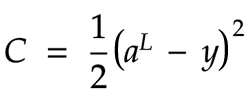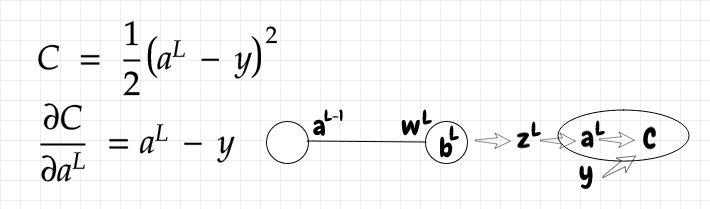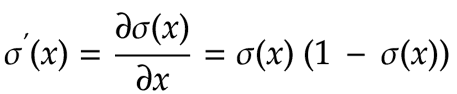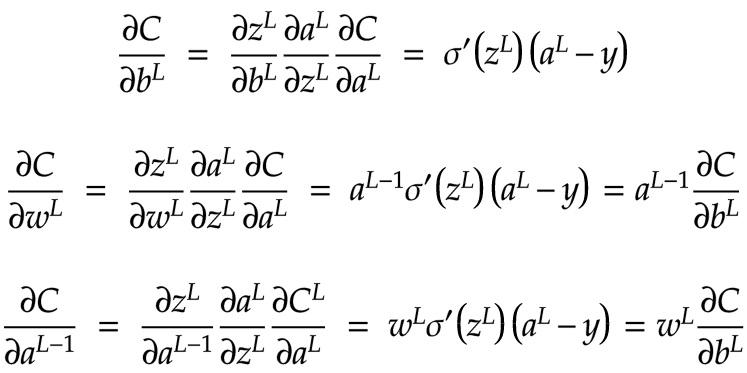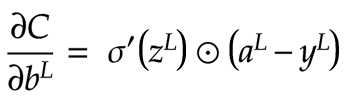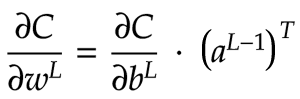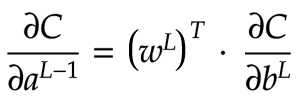神经网络入门

在本文中，我将介绍从零开始实现一个简单神经网络所需的基本概念。尽管以现代标准来看，这个神经网络还比较原始，但它仍然可以完成一些非常有用且令人印象深刻的事情：它可以被训练到准确识别 0 到 9 之间的手写数字！

我最近看了几个关于这个主题的教程。虽然这些教程都很棒，但看完之后我觉得有些地方还有进一步解释的空间。除了这篇入门指南之外，你也可以参考以下免费资源：

• 神经网络， 3Blue1Brown（Grant Sanderson）的 YouTube 视频系列
• 《神经网络和深度学习》第一章和第二章（迈克尔·尼尔森著）

神经网络结构

我们的神经网络结构非常简单。网络的基本单元是神经元。每个神经元可以接收来自任意数量神经元的输入。每个神经元产生一个输出值，这被称为该神经元的激活值。这个激活值可以作为输入发送给任意数量的其他神经元。

神经元被组织成层。给定层中的每个神经元接收来自前一层所有神经元的输入。给定神经元的激活也会发送到下一层的所有神经元。第一层称为输入层。最后一层称为输出层。介于两者之间的任何层都称为隐藏层，因为它们仅间接影响网络的最终输出。我们可以将其视为一条装配线：原材料进入输入层，最终产品从输出层的另一端出来。构建最终产品所涉及的所有中间步骤都发生在隐藏层中。下面是一个简单的图表，显示了神经网络的基本结构：

上面显示的网络有一个隐藏层，但通常有多个隐藏层。

连接两个神经元的边有两个关联值。一个是发送神经元的激活值，另一个是接收神经元赋予该激活值的权重。权重越高，传入的激活值对接收神经元激活值的影响就越大。一个给定的神经元可以从许多神经元接收输入，每个神经元都有自己的权重。每个神经元还有一个称为偏差的附加值。偏差衡量神经元的内在活跃程度。较高的正偏差意味着无论神经元接收到什么输入，它都倾向于具有更高的激活值。较高的负偏差将起到制动器的作用，显著抑制神经元的激活值。

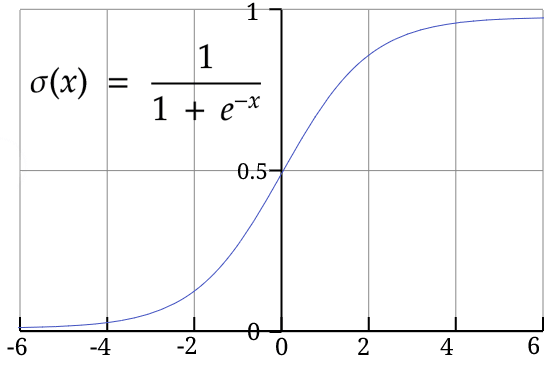
在这个例子中，我们将把给定神经元的激活值限制在 0 到 1 之间。为此，我们将使用S 型函数。该函数接受任何正数或负数作为输入，并将其压缩到 0 到 1 之间的范围内。以下是 S 型函数的示意图和公式：

Sigmoid 在神经网络早期曾被使用，但现在已不常用。如今，类似ReLU函数更为常见。

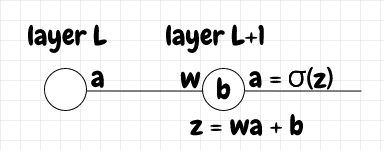
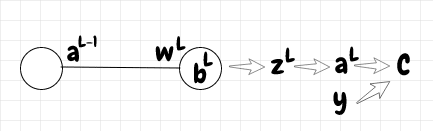
下面我们有一个最简单的情况，即L层中的单个神经元将信号输入到下一层L+1的神经元。为了计算L+1层神经元的激活值，首先我们将该边的权重乘以发送神经元的激活值，然后加上偏差。这成为一个原始激活值，在本文中我们将其称为z 。最后，我们将z应用于 S 型函数，以获得下一层L+1神经元的实际激活值a。

输入和输出

Grant Sanderson 将识别 MNIST 数字称为神经网络的入门。输入图像来自MNIST 数据库。每张 MNIST 图像都是一个28 x 28 的像素网格。每个像素都是 0 到 1 之间的十进制数，代表一个灰度值。下图中的数字6就是 MNIST 图像的示例：

为了将这些值作为网络的输入，我们只需将所有像素排列成一列，并将每个像素的灰度值分配给相应的输入神经元。这意味着我们需要28 x 28，即784 个输入神经元。

为了更清晰地理解，请看下图，图中数字2被表示为一个简单的6x6网格。真实的 MNIST 图像具有灰度值，但在本例中，网格单元要么是黑色，要么是白色（0 或 1）。为了生成输入层，我们将第一行像素指定为输入神经元，然后是下一行，依此类推。最终结果是，我们的输入由 36 个神经元表示：

我们用于识别手写数字的网络使用 10 个输出神经元，每个神经元的值介于 0 到 1 之间。我们希望与正确数字对应的输出神经元的值接近 1，而所有其他神经元的值尽可能接近 0。如果我们的图像代表数字4，那就意味着我们希望输出神经元的值接近[0, 0, 0, 0, 1, 0, 0, 0, 0]。

为什么我们要使用 10 个输出神经元？毕竟，我们可以压缩输出。例如，在二进制中，我们可以用 4 个神经元来编码从 0 到 10 的数字。这确实可行，但简化输出，使每个输出神经元只有一个含义，似乎更利于网络学习。从概念上讲，这意味着当我们增加或减少输出神经元的激活时，它只有一个含义。

下图展示了 Michael Nielsen 的书中实际用于识别 MNIST 图像的神经网络的概览：

图片来源：Michael A. Nielsen，《神经网络与深度学习》，Determination Press，2015 年

梯度下降

神经网络背后的关键思想是梯度下降。什么是梯度下降？假设你正在一片郁郁葱葱的山丘和草地中散步。假设你站在山顶，想要下到山谷。但是，你被蒙住了眼睛，看不到路。你怎样才能下到山脚下呢？一个简单的方法就是慢慢地在原地旋转，用脚摸索着找到你当前位置最陡峭的部分，然后沿着那个坡度向下迈一小步。从那里，你可以再次摸索着找到看起来最陡峭的下坡，然后朝那个方向再迈一小步，依此类推。最终，你会到达一个坡度逐渐减小的平坦区域。这种方法不能保证你一定能找到进入山谷的最佳路径，但它可以确保每一步都是相对于你当时所在位置的最佳移动。

简而言之，这就是神经网络使用的梯度下降方法！就这么简单。神经网络解决的每个问题，无论是图像和语音识别，还是围棋，或是预测股市，最终都表示为一个包含大量变量的函数。我们可以直观地将其视为一个巨大的（多维）图景。神经网络的任务就是迭代大量数据，以调整这些变量，使其能够沿着这个非常复杂的函数的斜率向下移动。

偏导数和梯度

让我们用一些简单的数学知识来探索梯度下降的概念。假设我们有一个函数f，它作用于一个变量x。当我们调整变量x时，函数f(x)的值也会随之变化。

如果我们现在位于某个点x ，我们如何沿着这个函数向下移动一步？我们可以通过对f求x的导数来计算函数的局部斜率。如果导数∂f(x)/x为正，则表示函数趋势向上。如果导数为负，则表示函数趋势向下。因此，我们可以使用以下伪代码计算向下移动的步长，其中是我们预先选定的一个小的增量值：step_size

step = ∂f(x)/x * step_size

x = x - step

• 如果∂f(x)/x为正，那么step也为正。因此，step从 中减去x会使 变x小。 变小x也会导致f(x)变小。换句话说，我们正在走下坡路。
• 如果导数为负，则导step数也为负。减去一个负值与加上一个正值相同，因此在这种情况下导数x会增加。由于斜率为负，因此增加导数x会导致下坡。

因此x = x - step，无论斜率是正还是负，都会帮助我们走下坡路。如果斜率为 0，则表示我们到达了一个平坦区域。这被称为函数的局部最小值。

∂f(x)/x表示如果我们对x进行微小的改变，它将对f(x)产生一定的影响。如果这个值很大（无论是正向还是负向），则表示斜率很陡。在x方向上的一小步移动会导致函数值向上或向下移动一大步。如果这个值接近于 0，则表示斜率相对平坦，因此在x方向上的一步移动不会对海拔高度产生太大的影响。

选择一个合适的值step_size取决于具体问题。太小会减慢网络的学习速度，但太大则可能意味着一步就能达到函数的更高点，而不是向下，这也是我们不希望看到的。由于它对学习的影响，在神经网络术语中，step_size它通常被称为学习率。它是一个超参数。“超参数”这个术语听起来很复杂，但它只是意味着学习率是一个必须手动调整的参数，而不是由网络在学习过程中自行优化。我们为神经网络选择的任何参数，如果之后没有经过网络学习过程的微调，就称为超参数。我们可以将超参数视为在开始学习过程之前可以调整的拨盘和旋钮。这些值会影响网络的学习过程，但训练网络的反馈回路不会改变这些参数。除非我们手动调整它们，否则它们会保持不变。

我们研究了单变量x的函数。这样的函数可以看作二维图像，一个轴表示x，另一个轴表示f(x)，如下图所示：

如果我们将函数增加到两个变量f(x,y)，那么我们需要为x和y各设置一个轴来表示输入，因此该函数可以看作是三维图像。该函数的斜率在三维中也变成一个向量。我们可以将该向量分解为两个分量向量，即沿x轴的斜率和沿y轴的斜率。这两个值∂f(x,y)/x和∂f(x,y)/y称为函数关于x和y的偏导数。换句话说，∂f(x,y)/x告诉我们如果对x进行微小调整而保持y不变，f(x,y)将发生多少变化。相反，∂f(x,y)/y告诉我们如果对y进行微小调整而保持x不变，f(x,y)将发生怎样的变化。偏导数的列表[∂f(x,y)/x, ∂f(x,y)/y]称为函数的梯度。它定义了函数在最速下降方向上的斜率，也就是说，将这些偏导数向量相加可以得到函数的总梯度向量。

这个想法也适用于具有大量参数的函数f(x,y,z,...)。事实上，这正是神经网络的运作方式。我们无法直接将此类函数可视化，但我们可以使用相同的数学工具来获取梯度。为了以小步长沿着这样的梯度向下移动，我们应用相同的技巧，即从每个变量中减去该变量的偏导数乘以某个小步长。每个轴的调整值将导致f(x,y,z...)更小。换句话说，这会使函数沿着相对于其当前位置的最陡下降路径向下移动。当我们稍后查看实现这一目标的数学时，我认为记住这一点会很有帮助，在高层次上，这就是正在发生的一切。

激活

让我们计算一下网络的输出。我们已经了解了如何计算只有一个输入的神经元的激活值。当一个神经元有多个神经元输入时，我们首先将输入神经元的加权激活值相加，然后加上偏差，最后应用我们的 S 型函数。换句话说，所有输入活动都会影响神经元的活跃程度。假设我们在L+1层有一个神经元，有两个神经元输入，如下图所示：

上标L和L+1并非指数。它们只是表示该值属于网络的哪一层。请记住，（几乎）本文中出现的上标并不表示指数！唯一的例外是 S 型函数及其导数，以及二次成本函数中用作指数的2 。

我们可以看到，我们将粉色和橙色神经元的加权激活相加，并加上蓝色神经元的偏差，得到了蓝色神经元的原始激活z：z = w _0,0 ^L+1 a ₀ ^L + w _0,1 ^L+1 a ₁ ^L + b ₀ ^L+1。然后我们应用 sigmoid 函数来获得激活：a = σ(z)。

事实证明，我们可以用矩阵巧妙地表达这个计算。我们用j表示L+1层的神经元，用k表示上一层L层的神经元。J表示L+1层的神经元总数，K表示L层的神经元总数。

j和k的这种排序可能看起来是向后的，但我们马上就会明白为什么使用这种索引方案。

让我们考虑一个简单的两层神经网络。第一层L有 2 个神经元，第二层L+1有 3 个神经元：

我们希望L+1层的激活是一个3x1矩阵，即一个单列三行的矩阵。每行的值代表该层对应神经元的激活值。为了将结果转化为合适的形式，我们可以定义所需的矩阵如下：

• 首先，我们将进入L ⁺¹层的权重定义为一个JxK矩阵w L +1。该矩阵的第一行包含进入L+1层第一个神经元的每个权重；第二行包含进入L+1层第二个神经元的每个权重，以此类推。

• 接下来，我们将L层中的激活分组为一个Kx1^的单列矩阵L。第一行表示来自L层第一个神经元的激活；第二行表示来自L层第二个神经元的激活，以此类推。

• 最后，我们将L+1层神经元的偏差放入一个Jx1 的单列矩阵b ^L+1中。第一行是L+1层第一个神经元的偏差；第二行是L+1层第二个神经元的偏差，以此类推。

我们可以看到，对w ^L+1 ⋅ a ^L进行点积运算会得到一个Jx1矩阵。我们可以将该矩阵加到b ^L+1上，同样是Jx1，从而得到一个Jx1矩阵z ^L+1，它包含了L+1层的所有原始激活值。最后，我们可以将z ^L+1中的每个值传递给 σ，从而得到一个包含^L+1层激活值的矩阵a L+1。

我们可以看到，我们需要对给定层L+1 的权重矩阵w进行排列，使得每一行对应于进入L+1层中给定神经元的边。这很直观，因为L+1层中神经元的激活取决于来自前一层的所有输入。这就是为什么我们使用j来索引下一层中的神经元，使用k来索引上一层中的神经元，因为我们希望权重矩阵是JxK矩阵。这样，点积就能计算出z和a矩阵的正确形状。如果我们反过来进行索引，我们的权重矩阵将是KxJ矩阵。这也很好，因为行和列的含义不会改变，只是命名方式不同。以下是计算z ^L+1和a ^L+1所需的矩阵计算：

计算两个矩阵的点积相当简单。两个矩阵必须具有I x J和J x K的形式，使得结果成为一个I x K矩阵。换句话说，左侧矩阵的列数必须与右侧矩阵的行数匹配。点积将变成一个行数与左侧矩阵相同、列数与右侧矩阵相同的矩阵。

成本函数

为了让网络学习，我们需要提供反馈，说明当前网络对于给定的训练输入是否表现良好。这通过使用成本函数来实现。成本函数将网络的实际输出与正确值进行比较。输出层可能有多个神经元。在这种情况下，我们需要将每个输出神经元的正确值与每个实际输出进行比较。在本例中，我们将使用一个简单的函数，称为二次成本函数：

据我所知，额外的除以2主要是为了抵消我们求该函数导数时得到的因子2。无论如何，这个常数因子不应该显著影响网络的学习方式。

如果我们的网络只有一个输出神经元，那么成本可以通过从输出值中减去正确值，然后对结果求平方来计算。如果我们有多个输出神经元，比如我们的 MNIST 数字识别网络中的 10 个神经元，那么我们可以将L ^（实际输出）和y（正确值）视为单列矩阵。在这种情况下，我们将这两个矩阵相减。这相当于对结果矩阵的每一行执行相同的减法。我们从每个给定神经元对应的实际输出中减去其预期值，然后对结果求平方。

对于给定的a和y值，如果我们将它们映射到一条线上的点，我们可以看到a - y是两点之间的距离，因此成本函数是该距离的平方。机器学习中还有其他成本函数。

反向传播

我们希望调整网络中的权重和偏差，以便随着时间的推移，训练数据产生的成本越来越低。为此，我们需要计算出成本函数相对于这些权重和偏差的斜率。然后，我们可以使用梯度下降法，使网络的每个反馈回路中的斜率小步下降。

让我们考虑一个最简单的场景：只有一个输出神经元，并且只有一个神经元从隐藏层输入信息。事实证明，我们针对这个简单情况推导的方程很容易推广到更普遍的每层多个神经元的情况。

在下图中，我们可以看到输出的成本C直接取决于激活a ^L以及该输入的预期值y。反过来，a ^L取决于原始激活z ^L。最后，z ^L取决于三个变量：偏差b ^L、权重w ^L和输入激活a ^L-1：

我们将利用这些信息来计算成本函数对权重和偏差的导数。我们还将计算成本函数对前一层神经元激活函数的导数。你可能想知道为什么我们需要计算相对于前一层激活函数的成本函数。毕竟，我们无法直接调整它。的确如此，我们无法直接修改神经元的激活函数。但是，我们可以使用相对于前一层激活函数的梯度来计算前一层所需的权重和偏差的调整，以此类推，在网络中向后移动。这就是为什么我们将调整所有权重和偏差的这一步骤称为反向传播。

我们首先计算成本函数关于输出神经元激活值的导数。这很简单，导数只是一个线性函数：

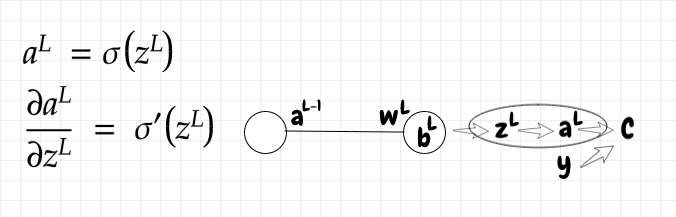
由于aL取决于zL ^，我们来计算一下a相对于z^的斜率：

S 型函数的导数为：

zL取决于来自前一层的输入激活aL ^{-1 、该激活的}权重wL以及^当前偏差bL。让我们计算z对以下每个输入的偏导数：

现在我们已经有了所需的所有偏导数，我们可以使用链式法则来计算网络反向传播所需的 3 个方程：成本函数关于权重、偏差和前一层激活的偏导数：

其原理是，我们可以使用w ^L和∂C/db ^L的值来计算∂C/∂a ^L-1。一旦有了∂C/∂a ^L-1，我们就可以用它来计算∂C/db ^L-1和∂C/dw ^L-1。从那里开始，我们只需在网络的各个层级中不断重复相同的步骤，直到到达输入层，这就是所谓的反向传播。

示例计算

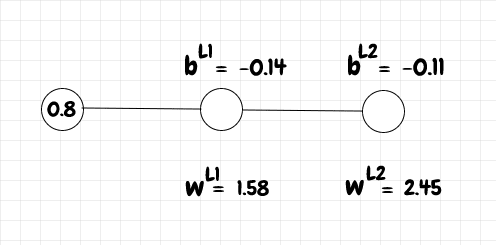
让我们计算一个小型网络的单次学习迭代，该网络包含一个输入神经元、一个中间神经元和一个输出神经元。我们将输入设置为0.8。该输入的预期输出y为 1。权重和偏差如下图所示：

首先，我们需要计算网络的原始激活值z以及激活值az 。我们使用以下 (python) 函数来计算、a和sigmoid：

import numpy as np

def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))

def z(w, a, b):
    return w * a + b

def a(z):
    return sigmoid(z)

对于L1z层，我们可以计算和的值，a如下所示：

>>> a_l0 = 0.8
>>> w_l1 = 1.58
>>> b_l1 = -0.14
>>> z_l1 = z(w_l1, a_l0, b_l1)
>>> a_l1 = sigmoid(z_l1)
>>> z_l1
1.124
>>> a_l1
0.7547299213576082

现在我们有了L1层的激活，我们可以使用它来计算zL2层a的：

>>> b_l2 = -0.11
>>> w_l2 = 2.45
>>> z_l2 = z(w_l2, a_l1, b_l2)
>>> a_l2 = sigmoid(z_l2)
>>> z_l2
1.73908830732614
>>> a_l2
0.850571226530534

太好了，现在我们得到了L2的激活函数。接下来我们需要计算成本函数关于三个变量的斜率：偏差、权重和前一层的激活函数。偏导数以及 S 型函数导数的公式sigmoid_prime如下：

def sigmoid_prime(z):
    return sigmoid(z)*(1-sigmoid(z))

def dc_db(z, dc_da):
    return sigmoid_prime(z) * dc_da

def dc_dw(a_prev, dc_db):
    return a_prev * dc_db

def dc_da_prev(w, dc_db):
    return w * dc_db

我们在下面计算这些偏导数：

>>> dc_da_l2 = a_l2-1
>>> dc_db_l2 = dc_db(z_l2, dc_da_l2)
>>> dc_dw_l2 = dc_dw(a_l1, dc_db_l2)
>>> dc_da_l1 = dc_da_prev(w_l2, dc_db_l2)
>>> dc_db_l2
-0.018992369482903983
>>> dc_dw_l2
-0.014334109526226761
>>> dc_da_l1
-0.04653130523311476

现在我们有了成本函数关于偏差b_l2和权重的斜率w_l2，我们可以更新这些偏差和权重：

>>> step_size = 0.1
>>> updated_b_l2 = b_l2 - dc_db_l2 * step_size
>>> updated_w_l2 = w_l2 - dc_dw_l2 * step_size
>>> updated_b_l2
-0.1081007630517096
>>> updated_w_l2
2.451433410952623

调整完L2层的权重和偏差后，我们可以对L1层进行同样的操作。我们计算了dc_da_l1，它是成本函数相对于来自前一层的激活函数的斜率。为了获得L1层偏差和权重的梯度，我们只需像之前一样继续使用链式法则即可。在L2层中，dc_da_l2是a_l2-y。对于L1层，我们刚刚计算了，因此我们现在可以用它来获得成本函数相对于L1dc_da_l1层偏差的斜率，即 。然后我们像之前一样继续，使用来计算。dc_db_l1dc_db_l1dc_dw_l1

>>> dc_db_l1 = dc_db(z_l1, dc_da_l1)
>>> dc_dw_l1 = dc_dw(a_l0, dc_db_l1)
>>> dc_db_l1
-0.008613534018377424
>>> dc_dw_l1
-0.006890827214701939

再次，我们使用这些偏导数来调整 L1 的权重和偏差：

>>> updated_b_l1 = b_l1 - dc_db_l1 * step_size
>>> updated_w_l1 = w_l1 - dc_dw_l1 * step_size
>>> updated_b_l1
-0.13913864659816227
>>> updated_w_l1
1.5806890827214704

我们不需要进一步深入，因为L0层是输入层，我们无法调整它。让我们使用更新后的权重和偏差来计算新的激活：

>>> updated_z_l1 = z(updated_w_l1, a_l0, updated_b_l1)
>>> updated_a_l1 = sigmoid(updated_z_l1)
>>> updated_z_l1
1.125412619579014
>>> updated_a_l1
0.7549913210309638
>>> updated_z_l2 = z(updated_w_l2, updated_a_l1, updated_b_l2)
>>> updated_a_l2 = sigmoid(updated_z_l2)
>>> updated_z_l2
1.7427101863028525
>>> updated_a_l2
0.8510309824120517

最后，让我们比较一下原始激活函数和使用新激活函数得到的损失函数。我们将使用以下公式作为损失函数：

def cost(a, y):
    return 0.5 * (a - y)**2

原始成本和更新成本为：

>>> original_cost = cost(a_l2, 1)
>>> updated_cost = cost(updated_a_l2, 1)
>>> original_cost
0.011164479170294499
>>> updated_cost
0.011095884100559231

我们可以看到，updated_cost确实比略低一点original_cost！

每层多个神经元

当我们的网络每层有多个神经元时，像w、b、z和a这样的量就变成了矩阵，而不是标量。为了适应这种情况，我们需要对用于偏导数的方程进行一些调整。新方程式的优点在于它的形式非常直观。我们只需想象我们想要的矩阵形状，就能推导出方程的形式。

让我们考虑一个如下所示的简单多层网络。您可以看到每层中各个矩阵的形状：

请记住，上标均表示当前层。它们不是指数。

由于我们知道每个偏差都会用偏导数来更新，所以我们需要为每个偏差都对应一个偏导数值。因此，成本函数对当前层偏差的偏导数∂C/∂b应该与该层的偏差矩阵具有相同的形状。

在我们的例子中，输出层有 2 个神经元，所以该层的偏差矩阵b是一个2x1矩阵。因此该层的∂C/∂b也应该是 2x1 矩阵。从我们之前推导的方程式中，我们知道∂C/∂b要求我们将(ay)和σ'(z)的值相乘。这两个都是2x1矩阵，所以我们需要做的就是将每个神经元的σ'(z)值乘以同一个神经元的差值(ay)。直观上这是有道理的：(ay)中的每个值都与其对应的σ'(z)值匹配。当给定值与一堆输入或输出值相关时，我们使用点积，但在这里它们是简单的 1:1 关系。两个相同矩阵的这种简单乘积称为Hadamard 积。我们将其表示为一个被圆圈包围的点。以下是∂C/∂b方程的矩阵形式：

现在让我们将注意力转向∂C/∂w。在我们的输出层中，权重矩阵w是一个2x3矩阵。因此，我们希望∂C/∂w也是一个 2x3 矩阵。当前层的∂C/∂w是当前层的∂C/∂b与前一层的激活矩阵a 的乘积。对于我们的输出层， ∂C/∂b是一个2x1矩阵。前一层的a是一个3x1矩阵。我们不能直接将2x1和3x1矩阵相乘。但是，我们可以转置a将其转换为1x3矩阵！现在，使用点积的乘法将生成一个2x3矩阵。这与该层的w矩阵的形状相匹配，因此可以正常工作。以下数学符号显示了如何以矩阵形式获得∂C/∂w ：

最后，我们需要计算∂C/∂a ^L-1。a L ^-1是一个3x1矩阵，因此我们希望∂C/∂a ^L-1也是一个3x1矩阵。我们知道需要以某种方式将∂C/∂b与当前层的权重矩阵w相乘。∂C /∂b是一个2x1矩阵，w是一个2x3矩阵。我们如何将它们乘积起来以获得3x1矩阵？我们可以先转置w以获得3x2矩阵。现在我们可以对3x2矩阵w ^T和2x1矩阵∂C/∂b进行点积，这样就得到了我们想要的3x1矩阵。公式如下图所示：

最后一个矩阵表示成本函数相对于前一层激活函数的斜率。这非常有用，因为我们可以用这个值来计算相对于前一层的偏差∂C/∂b和权重∂C/∂w的斜率。这些值又可以用来计算∂C/∂a ^L-2，依此类推。我们继续逐层执行相同的操作，直到到达输入层。回想一下，我们不计算输入层的任何偏导数，因为这不是网络需要调整的部分。

如果你想直观地理解为什么我们要转置w并进行点积运算，我觉得这样理解会很有帮助：当我们计算给定层的激活矩阵时，我们会计算该层的权重矩阵与前一层激活矩阵的点积。这是有道理的，因为对于下一层中的每个神经元，它需要将前一层所有神经元的加权激活值汇总在一起。我们可以将∂C/∂a ^L-1视为这枚硬币的另一面。当我们对当前层中某个神经元的激活值进行微小调整时，它将沿着多条路径影响成本函数。假设我们调整一个连接到下一层中 3 个神经元的神经元的激活值。我们需要将发送神经元对成本函数的影响加到第一个接收神经元、第二个接收神经元和第三个接收神经元上。这将是我们结果矩阵的第一行（对于发送层中的其他每个神经元，依此类推）。因此，我们需要一个矩阵，其中每一行代表前一层神经元的激活变化对下一层每个神经元的累积效应。

这种方法使我们能够计算网络每一层的权重和偏差的调整，并从输出层向后传播。一旦针对给定输入完成该过程，我们就可以说网络完成了一个训练步骤。通过对大量输入进行这种训练，我们可以稳步调整网络参数，直到它能够完成像识别 MNIST 图像这样的酷炫任务！

下图显示了我们的示例网络，其中包含输出层和中间层的偏导数：

请记住，上标均表示当前层。它们不是指数。

我用 Python 编写了一个非常简单的神经网络实现。我尽量去掉了所有无关的细节，只展示了前馈激活函数以及调整权重和偏差所需的代码，每次只针对一个训练输入：

import numpy as np

placeholder = np.array([[]])

class Network:
    def __init__(self, layers, **kw):
        self.num_layers = len(layers)
        self.b = [placeholder]
        self.w = [placeholder]

        if "b" in kw:
            b = kw.get("b")
            self.b += b

        if "w" in kw:
            w = kw.get("w")
            self.w += w

        num_neurons_prev_layer = layers[0]
        for num_neurons_current_layer in layers[1:]:
            if not "b" in kw:
                b = np.random.randn(num_neurons_current_layer, 1)
                self.b.append(b)

            if not "w" in kw:
                w = np.random.randn(num_neurons_current_layer, num_neurons_prev_layer)
                self.w.append(w)

            num_neurons_prev_layer = num_neurons_current_layer

    def feed_forward(self, inputs):
        self.z = [placeholder]
        self.a = [np.asarray([inputs]).transpose()]

        for l in xrange(1, self.num_layers):
            b = self.b[l]
            w = self.w[l]
            a_prev = self.a[l-1]

            z = raw_activation(w, a_prev, b)
            a = sigmoid(z)

            self.z.append(z)
            self.a.append(a)

    def propagate_backward(self, y, step_size):
        y = np.asarray([y]).transpose()

        output_layer = self.num_layers-1
        z = self.z[output_layer]
        a = self.a[output_layer]

        activations_gradient = a - y
        biases_gradient = dc_db(z, activations_gradient)

        a_prev = self.a[output_layer-1]
        weights_gradient = dc_dw(a_prev, biases_gradient)

        w = self.w[output_layer]
        activations_gradient = dc_da_prev(w, biases_gradient)

        self.b[output_layer] -= biases_gradient * step_size
        self.w[output_layer] -= weights_gradient * step_size

        for l in xrange(self.num_layers-2, 0, -1):
            z = self.z[l]
            biases_gradient = dc_db(z, activations_gradient)

            a_prev = self.a[l-1]
            weights_gradient = dc_dw(a_prev, biases_gradient)

            w = self.w[l]
            activations_gradient = dc_da_prev(w, biases_gradient)

            self.b[l] -= biases_gradient * step_size
            self.w[l] -= weights_gradient * step_size

def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    return sigmoid(z)*(1-sigmoid(z))

def raw_activation(w, a, b):
    return np.dot(w,a) + b

def dc_db(z, dc_da):
    return sigmoid_prime(z) * dc_da

def dc_dw(a_prev, dc_db):
    return np.dot(dc_db, a_prev.transpose())

def dc_da_prev(w, dc_db):
    return np.dot(w.transpose(), dc_db)

# demo:
b = [np.array([[0.54001045],
               [0.75958375],
               [0.01870296]]),
     np.array([[-0.32783478],
               [ 0.06061246]])]

w = [np.array([[-0.11499179,  0.454649  ],
               [-0.65801895,  0.56618695],
               [-0.15686814, -0.87499479]]),
     np.array([[ 0.01071228, -0.49139708, -0.81775586],
               [-0.87455946, -0.08351883, -0.77534763]])]

n = Network([2,3,2], b=b, w=w)

inputs = [0.8,0.2]
n.feed_forward(inputs)

y = [0, 1]
n.propagate_backward(y, 0.1)

请注意，我们通常会随机化权重和偏差的初始值。这是一种简单的方法，可以创建一个相当混乱的初始成本函数，并为梯度下降留出充足的空间。我们不想冒险以某种可预测的方式设置这些变量，这可能会从一开始就将成本函数置于一个平面上！

想想看，这段代码基本上足以识别 MNIST 数字的手写图像，成功率高达 95% 左右！这真是太了不起了。想象一下，开发一个自定义算法来实现同样的效果需要付出多少努力。我认为用这种方法达到同样的准确率会非常困难，但使用上面这个非常简单的实现方法，我们就能取得相当不错的效果：我们只需要用完全通用的方式将多层神经元连接在一起，大概 100 行代码就能完成前向和后向传播！

随机梯度下降

像上面的代码一样，针对每个输入调整所有的权重和偏差可能会很慢。一种常见的加速技术是通过网络运行一批输入，并将其视为一个训练步骤。换句话说，首先，我们计算一堆随机选择的训练输入的偏导数。我们不断将最新的偏导数添加到每个梯度矩阵中。完成后，我们将每个累积的偏导数除以批次中的样本数。然后，我们根据这个平均斜率更新一次权重和偏差。然后，我们可以对另一批输入继续做同样的事情。这称为随机梯度下降。直观地说，这意味着我们沿着景观斜坡向下移动时会比其他情况下更加不平稳。如果我们在每次输入后调整所有参数，那么我们向下的路径将是一条更平滑的曲线，但计算时间会更长。

MNIST图像识别

Michael Nielsen 的Python 代码（github）用于识别 MNIST 图像，只需在普通 PC 上训练几分钟，就能轻松达到约 95% 的识别率。以下脚本运行一个包含 30 个神经元的单隐藏层的网络（run.py）：

import mnist_loader
import network

training_data, validation_data, test_data = mnist_loader.load_data_wrapper()

net = network.Network([784, 30, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)

以下结果显示该网络实现了接近 95％ 的准确率：

C:\Dev\python\neural-networks-and-deep-learning\src>python run.py
Epoch 0: 9032 / 10000
...
Epoch 29: 9458 / 10000

如果我们将网络改为 2 个隐藏层，每个隐藏层有 16 个神经元，就像 Grant Sanderson 的视频 (run2.py) 中那样：

import mnist_loader
import network

training_data, validation_data, test_data = mnist_loader.load_data_wrapper()

net = network.Network([784, 16, 16, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)

结果似乎大致相同：

C:\Dev\python\neural-networks-and-deep-learning\src>python run2.py
Epoch 0: 8957 / 10000
...
Epoch 29: 9385 / 10000

如果我们完全省略隐藏层，只是将输入层直接发送到输出层，那么准确率就会下降很多，降至 75%。

在他的视频中，格兰特·桑德森（Grant Sanderson）对不同层的概念含义进行了一些推测。他提出了一个想法：第一个隐藏层可能识别手写数字基本单位的各个部分。例如，它可能会将“o”形环分解成几个部分。第二个隐藏层可能会将这些单独的部分组合在一起，例如，数字“ 9”可能是一个“o”形环，环外延伸出一条直线或曲线。

然而，格兰特发现，检查隐藏层并没有发现任何如此明确的东西，只是一些相当嘈杂的数据，只显示出一些模式的迹象。这表明，这个神经网络不必寻找对我们人类有意义的最小值。它似乎找到了足以相当好地解决问题的局部最小值，但这些最小值并不能完全概括数字的含义。也就是说，正如格兰特所说，在深不可测的13,000维权重和偏差空间中，我们的网络找到了一个令人满意的小局部最小值，尽管成功地对大多数图像进行了分类，但并没有完全捕捉到我们所希望的模式……即使这个网络可以很好地识别数字，它也不知道如何绘制它们。这一事实的一个结果是，我们的特定网络对随机像素图像的分类与对真正的MNIST图像一样自信！

我们这个简单的网络显然存在局限性。例如，隐藏层似乎没有任何清晰的模式或含义。此外，由于每层都包含大量神经元，将上一层的每个神经元连接到下一层的所有神经元可能会造成性能问题。而且，所有输入神经元无论彼此靠近还是位于图像的两侧，都被一视同仁，这难道不奇怪吗？

这些问题都是一些随着时间的推移而发展起来的更复杂的神经网络方法所要解决的。如果您想深入了解，可以查看深度学习、卷积神经网络、循环神经网络和长短期记忆网络等进一步的发展。综上所述，我们在本文中讨论的简单网络的一个优点是，它已经可以完成一些有用的任务，而且非常容易理解！