二分查找

二分查找是最快的搜索算法之一，尤其是在搜索大型（已排序）列表时。
二分查找的主要目标是尽可能缩小搜索范围，从而减少查找步骤。

实现二分查找时，您应该：
1- 假设您正在处理已排序的列表——否则，查找将无法进行。2-
指定搜索的起始点和结束点。3-
从列表中间选取一个元素，并将其与要查找的元素进行比较。根据比较结果，您应该知道是否找到了该元素，或者是否需要修改起始点和结束点并重复上述步骤。

让我们看一个例子。

 function binarySearch(list, itemToFind){
   // some code to return the index of itemToFind
 }
  let list = [10, 21, 25, 30, 32, 35, 50, 52, 55, 60];
  let itemToFind = 32; 
  binarySearch(list, itemToFind) // should return the index of 32.

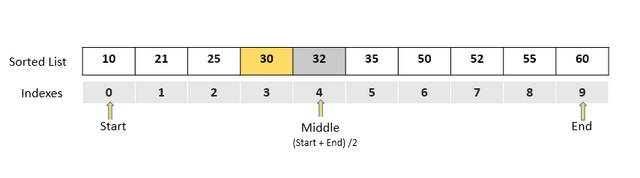
要实现中的代码binarySearch，我们首先需要设置起点和终点。由于我们需要覆盖整个列表，因此需要将初始起点指定为列表的第一个索引，将终点指定为列表的最后一个索引。

  let start = 0;
  let end = list.length -1; // 9

接下来，我们需要设置一个中间点索引，然后将其值与我们正在搜索的项目进行比较。

   let middle = Math.floor((start + end)/2); // 4
   if (list[middle] === itemToFind) return middle;

由于我们搜索的是恰好位于列表中间的元素，这几行代码会itemToFind立即返回元素的索引。这被称为best-case scenario算法的——你的第一个猜测就是正确答案。

但当然，这种情况很少发生，所以我们需要考虑在列表中间找不到我们的物品的情况。

我们开始新的搜索，这次搜索 30。

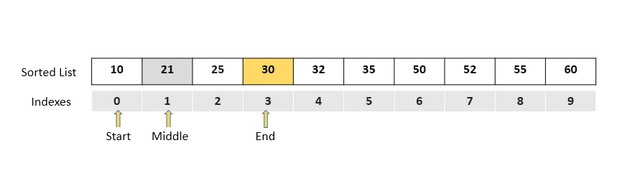
嗯，我们和以前一样计算了中间点，但不幸的是，我们没有在那里找到 30。

现在，我们知道中间项不等于itemToFind。但它大于还是小于itemToFind？

我们发现 32 大于 30。那么这是什么意思呢？

由于list已排序，这意味着itemToFind一定位于start和之间middle。

下一步：重新定位end搜索点以缩小搜索窗口。

  if(middle > itemToFind){
    end = middle -1;
  }

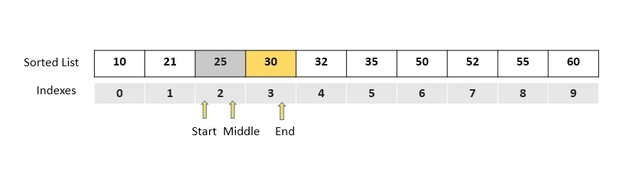
然后重新计算middle并检查新的中间值。

   if (list[middle] === itemToFind) return middle; 
   if(middle > itemToFind) end = middle -1; // 3
   middle = Math.floor((start + end)/2); // 1

中间项现在是21。它不等于 30，所以我们无法返回它的索引。它不大于 30，所以通过重新定位end来缩小搜索范围是不可能的。但是，我们可以重新定位start。因为此时，如果该项存在，它一定位于middle和之间end。

  if(list[middle] < itemToFind){
    start = middle + 1;
  }

然后重新计算middle并检查新的中间值。

   if(list[middle] === itemToFind) return middle; 
   if(list[middle] > itemToFind) end = middle -1; // 3
   if(list[middle] < itemToFind) start = middle + 1; // 2
   middle = Math.floor((start + end)/2); // 2

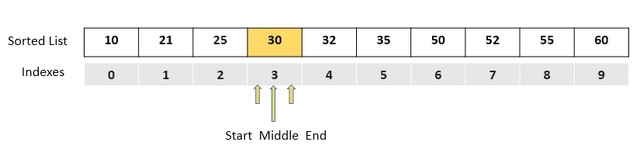
我们发现是 25 。它仍然小于 30 。因此我们重新定位start，计算middle，然后再次检查。

最后，middle指向我们要搜索的物品。然而，这是在我们用尽所有搜索选项之后发生的，此时我们的搜索窗口start位于它所end在的位置。这意味着我们在worst-case scenario算法的末端找到了我们的物品——这是你最后一次猜测正确答案的机会。

注意itemToFind：如果不存在，也会发生最坏的情况list。

关于二分查找我最后要提到的一点是它具有O(log n)时间复杂度，这意味着log n在最坏的情况下找到一个项目需要时间。

// final implemtation
function binarySearch(list, itemToFind) {
  let start = 0;
  let end = list.length - 1;
  while (start <= end) {
    let middle = Math.floor((start + end) / 2);
    if (list[middle] === itemToFind) return middle;

    if (list[middle] > itemToFind) {
      end = middle - 1;
    } else {
      start = middle + 1;
    }
  }
  return -1; // not found
}

（感谢阅读）

鏂囩珷鏉ユ簮锛�https://dev.to/hajarnasr/binary-search-scribbles-67k