50 个 Python 面试问题及答案
这篇文章由 Cameron Wilson 撰写,最初发表于Educative.io
这篇文章将涵盖 Python 编程语言的面试题。虽然这份清单并不详尽,但它应该能让你大致了解面试中可能会遇到哪些类型的问题。
以下是将要涉及的问题列表:
Python语言基础
- 问题1:列表和元组有什么区别?
- 问题 2:如何将列表转换为元组?
- 问题3:数组和列表有什么区别?
- 问题 4:如何将列表转换为数组?
- 问题5:Python中如何管理内存?
- 问题6:如何在Python中实现多线程?
- 问题 7:什么是猴子补丁?
- 问题 8:什么是 lambda 函数?请举例说明它何时有用,何时没用。
- 问题 9:什么是酸洗和反酸洗?
- 问题 10:NumPy 数组与(嵌套)Python 列表相比有哪些优势?
- 问题 11:通过示例解释 Python 中的继承
- 问题 12:Python 中的多态性是什么?
- 问题 13:解释 range() 和 xrange() 之间的区别
- 问题 14:解释 Flask 和 Django 之间的区别
- 问题 15:什么是 PYTHONPATH?
- 问题 16:什么是 PEP 8?
- 问题 17:什么是 Python 装饰器?
- 问题18:什么是init?
- 问题 19:什么是三元运算符?
- 问题 20:Python 中的全局变量和局部变量是什么?
- 问题 21:Python 中的 @property 是什么?
- 问题 22:Python 中如何使用 try/except?
- 问题 23:解释 Python 2 和 Python 3 之间的区别
- 问题 24:python 中的 join 方法是什么?
- 问题 25:什么是词典理解?
- 问题 26:如何在 Python 中进行深层复制?
- 问题 27:如何检查 Python 字典中是否存在某个键?
- 问题 28:如何在 Python 中实现记忆化?
- 问题 29:如何在 Python 中对字典进行排序?
- 问题 30:如何以及何时使用 any() 和 all()?
- 问题 31:什么是 Python Docstring?
- 问题 32:编写一个 Python 函数并解释发生了什么。
- 问题 33:解释 Python 中生成器和迭代器之间的区别。
- 问题 34:Python 中的 defaultdict 是什么?
- 问题 35:什么是 Python 模块?
Python编码问题
- 问题 36:在 Python 中反转字符串
- 问题 37:检查 Python 字符串是否包含另一个字符串
- 问题 38:在 Python 中实现广度优先搜索(BFS)
- 问题 39:在 Python 中实现深度优先搜索(DFS)
- 问题 40:在 Python 中实现通配符
- 问题 41:在 Python 中实现合并排序
- 问题 42:用 Python 实现 Dijkstra 算法
- 问题 43:合并两个排序列表
- 问题 44:找出两个加起来等于 'k' 的数字
- 问题 45:查找列表中第一个不重复的整数
- 问题 46:找出链表的中间值
- 问题 47:反转队列的前 ‘k’ 个元素
- 问题 48:求二叉搜索树(BST)的高度
- 问题 49:将最大堆转换为最小堆
- 问题 50:检测链表中的循环
Python 面试问题 - 特定语言
问题1:列表和元组有什么区别?
| 列表 | 元组 |
|---|---|
| 列表由可变对象组成。(创建后可以更改的对象) | 元组由不可变对象组成。(创建后无法更改的对象) |
| List 具有较大的内存。 | Tuple 的内存很小。 |
| 列表存储在两个内存块中(一个是固定大小,另一个是可变大小,用于存储数据) | 元组存储在单个内存块中。 |
| 创建列表较慢,因为需要访问两个内存块。 | 创建元组比创建列表更快。 |
| 列表中的元素可以被删除或替换。 | 元组中的元素不能被删除或替换。 |
| 列表的数据存储在 [] 括号中。例如,[1,2,3] | 元组的数据存储在 () 括号中。例如,(1,2,3) |
何时使用:
只要用户知道元组中插入了什么,就应该使用元组。假设一所大学将其学生的信息存储在一个数据结构中;为了使这些信息保持不变,就应该将其存储在元组中。
由于列表为用户提供了更便捷的访问方式,因此当需要存储类似类型的对象时,就应该使用列表。例如,如果杂货店需要将所有乳制品存储在一个字段中,就应该使用列表。
问题 2:如何将列表转换为元组?
my_list = [50, "Twenty", 110, "Fifty", "Ten", 20, 10, 80, "Eighty"]
my_tuple = (my_list[0], my_list[len(my_list) - 1], len(my_list))
print(my_tuple)
输出:(50,'Eighty',9)
我们只需创建一个包含三个元素的元组。元组的第一个元素就是列表的第一个元素,可以使用 找到my_list[0]。
元组的第二个元素是列表中的最后一个元素。my_list[len(my_list) - 1]将返回此元素。 我们也可以使用该pop()方法,但这会改变列表。
问题3:数组和列表有什么区别?
| 列表 | 大批 |
|---|---|
| Python 列表非常灵活,可以保存任意数据。 | Python 数组只是 C 数组的一个薄包装器。 |
| 列表是 Python 语法的一部分,因此不需要先声明。 | 首先需要从其他库(即 numpy)导入或声明数组。 |
| 列表还可以快速高效地调整大小。这是因为 Python 在初始化时会初始化列表中的一些额外元素。 | 数组无法调整大小。相反,需要将数组的值复制到另一个更大的数组中。 |
| 列表可以保存异构数据。 | 数组只能存储同质数据。它们的值具有统一的数据类型。 |
| 数学函数不能直接应用于列表。相反,它们必须分别应用于每个元素。 | 数组针对算术计算进行了特别优化。 |
| 列表会消耗更多内存,因为它们分配了一些额外的元素以便更快地添加项目。 | 由于数组保持其首次初始化时的大小,因此它们是紧凑的。 |
问题 4:如何将列表转换为数组?
在编程过程中,有时您需要将现有列表转换为数组才能对其执行某些操作(数组可以以列表无法实现的方式对其执行数学运算)。
这里我们将使用numpy.array()。numpy
库的这个函数接受一个列表作为参数,并返回一个包含该列表所有元素的数组。请参阅以下示例:
import numpy as np
my_list = [2,4,6,8,10]
my_array = np.array(my_list)
# printing my_array
print my_array
# printing the type of my_array
print type(my_array)
输出:
[2 4 6 8 10]
问题5:Python中如何管理内存?
- Python 中的内存管理由 Python 私有堆空间管理。所有 Python 对象和数据结构都位于私有堆中。程序员无法访问这个私有堆。Python 解释器会负责处理此事。
- Python 对象的堆空间分配由 Python 的内存管理器完成。核心 API 为程序员提供了一些工具来编写代码。
- Python 还具有内置的垃圾收集器,它可以回收所有未使用的内存,以便将其提供给堆空间。
问题6:如何在Python中实现多线程?
- Python 有一个多线程包,但是如果您想使用多线程来加快代码速度,那么使用它通常不是一个好主意。
- Python 有一个称为全局解释器锁 (GIL) 的结构。GIL 确保同一时刻只有一个“线程”可以执行。一个线程获取 GIL,执行一些工作,然后将 GIL 传递给下一个线程。
- 这发生得非常快,所以在人眼看来,你的线程似乎在并行执行,但实际上它们只是轮流使用同一个 CPU 核心。
- 所有这些 GIL 传递都会增加执行开销。这意味着,如果你想让代码运行得更快,使用线程包通常不是一个好主意。
问题 7:什么是猴子补丁?
在 Python 中,术语 monkey patch 仅指运行时对类或模块的动态修改。
问题 8:什么是 lambda 函数?请举例说明它什么时候有用,什么时候没用。
Lambda 函数是一个小型匿名函数,它返回一个对象。
lambda 返回的对象通常被分配给变量或用作其他更大函数的一部分。
与创建函数时使用的常规 def 关键字不同,lambda 函数是使用 lambda 关键字来定义的。lambda 的结构如下所示:
Lambda 的用途
Lambda 表达式比完整函数更具可读性,因为它可以内联编写。因此,当函数表达式较短时,使用 Lambda 表达式是一种很好的做法。
Lambda 函数的美妙之处在于它返回函数对象。这使得它们在与map或filter等需要函数对象作为参数的函数一起使用时非常有用。
当表达式超过一行时,Lambda 就没用了。
问题 9:什么是酸洗和反酸洗?
Pickle 模块接受任何 Python 对象,并将其转换为字符串表示形式,然后使用 dump 函数将其转储到文件中,此过程称为 pickling。而从存储的字符串表示形式中检索原始 Python 对象的过程称为 unpickling。
继续学习。
练习最常见的 Python 面试题,提升你的自信心。Educative 的文本课程易于浏览,并提供实时浏览器编程环境,让学习更快速、更高效。
问题 10:NumPy 数组与(嵌套)Python 列表相比有哪些优势?
- Python 的列表是高效的通用容器。它们支持(相当)高效的插入、删除、追加和连接操作,并且 Python 的列表推导式使其易于构建和操作。
- 它们有一定的局限性:它们不支持“矢量化”运算,如元素加法和乘法,而且它们可以包含不同类型的对象,这意味着 Python 必须为每个元素存储类型信息,并且必须在对每个元素进行操作时执行类型分派代码。
- NumPy 不仅更高效,也更便捷。它提供了大量的向量和矩阵运算,有时可以避免不必要的工作。而且这些运算的实现也非常高效。
- NumPy 数组速度更快,并且您可以获得 NumPy 内置的大量功能,包括 FFT、卷积、快速搜索、基本统计、线性代数、直方图等。
问题 11:通过示例解释 Python 中的继承
继承允许一个类获得另一个类的所有成员(例如属性和方法)。继承提供了代码可重用性,使应用程序的创建和维护更加容易。我们继承的类称为超类,被继承的类称为派生类/子类。
它们是 Python 支持的不同类型的继承:
- 单一继承——派生类获取单个超类的成员。
- 多级继承——派生类 d1 继承自基类 base1,派生类 d2 继承自 base2。
- 层次继承——从一个基类可以继承任意数量的子类
- 多重继承——派生类从多个基类继承。
问题 12:Python 中的多态性是什么?
多态性是指能够呈现多种形态的能力。例如,如果父类有一个名为 ABC 的方法,那么子类也可以有一个同名的方法 ABC,并且拥有自己的参数和变量。Python 支持多态性。
range()问题 13:解释和之间的区别xrange()
在大多数情况下,xrange 和 range 在功能上完全相同。它们都提供了一种生成整数列表供您使用的方法。唯一的区别是 range 返回一个 Python 列表对象,而 xrange 返回一个 xrange 对象。
这意味着 xrange 实际上不会像 range 那样在运行时生成静态列表。它会使用一种名为 yielding 的特殊技术,根据需要创建值。此技术与一种称为生成器的对象类型一起使用。
问题 14:解释 Flask 和 Django 之间的区别
Django是一个 Python Web 框架,它提供了一个开源的高级框架,旨在“鼓励快速开发和简洁实用的设计”。它快速、安全且可扩展。Django 提供强大的社区支持和详尽的文档。
该框架是一个包罗万象的软件包,您可以在创建应用程序时立即获得管理面板、数据库接口和目录结构。此外,它包含许多功能,因此您无需添加单独的库和依赖项。它提供的功能包括用户身份验证、模板引擎、路由、数据库模式迁移等等。
Django 框架非常灵活,您可以从最小可行产品 (MVP) 到大型公司进行开发。从某些角度来看,使用 Django 的大型公司包括 Instagram、Dropbox、Pinterest 和 Spotify。
Flask 被认为是一个微框架,即一个极简的 Web 框架。它的功能并不那么“齐全”,这意味着它缺少 Django 等全栈框架提供的许多特性和功能,例如 Web 模板引擎、帐户授权和身份验证。
Flask极简轻量,这意味着您可以在编写代码时添加所需的扩展和库,而无需框架自动提供。Flask 背后的理念是,它只提供构建应用所需的组件,从而让您拥有灵活性和控制力。换句话说,它没有固执己见。它提供的功能包括内置开发服务器、Restful 请求调度、Http 请求处理等等。
问题 15:什么是 PYTHONPATH?
它是一个环境变量,在导入模块时使用。每当导入模块时,都会查找 PYTHONPATH 来检查导入的模块是否存在于各个目录中。解释器使用它来确定要加载哪个模块。
问题 16:什么是 PEP 8?
PEP 代表 Python 增强提案。它是一组规则,指定如何格式化 Python 代码以实现最大可读性。
问题 17:什么是 Python 装饰器?
装饰器是 Python 中的一种设计模式,它允许用户在不修改现有对象结构的情况下为其添加新功能。装饰器通常在要装饰的函数定义之前调用。
问题18:什么是init?
__init__是 Python 中的一个方法或构造函数。当创建类的新对象/实例时,会自动调用此方法来分配内存。所有类都有此__init__方法。
问题 19:什么是三元运算符?
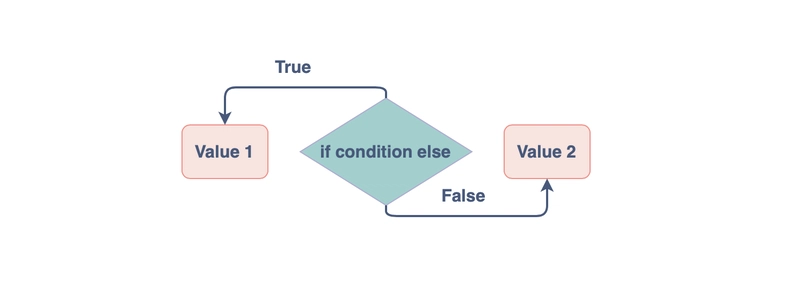
三元运算符是 Python 中编写条件语句的一种方式。顾名思义,该 Python 运算符由三个操作数组成。
注意:三元运算符可以被认为是用于测试条件的 if-else 语句的简化单行版本。
句法
三元运算符中的三个操作数包括:
- 条件:计算结果为真或假的布尔表达式。
true_val:表达式计算结果为真时要分配的值。false_val:当表达式计算结果为假时要分配的值。
var = true_val if condition else false_val
var赋值运算符左侧的变量=将被赋值:
value1如果 booleanExpression 计算结果为true。value2如果 booleanExpression 计算结果为false。
例子
# USING TERNARY OPERATOR
to_check = 6
msg = "Even" if to_check%2 == 0 else "Odd"
print(msg)
# USING USUAL IF-ELSE
msg = ""
if(to_check%2 == 0):
msg = "Even"
else:
msg = "Odd"
print(msg)
输出:
均匀
均匀
解释
上面的代码使用三元运算符来判断一个数字是偶数还是奇数。
msg如果条件 (to_check % 2 == 0) 成立,则将被分配为“even”true。msg如果条件 (to_check % 2 == 0) 成立,则将被分配为“奇数”false。
问题 20:Python 中的全局变量和局部变量是什么?
全局变量:
在函数外部或全局空间中声明的变量称为全局变量。这些变量可以被程序中的任何函数访问。
局部变量:
任何在函数内部声明的变量都称为局部变量。此类变量存在于局部空间,而不存在于全局空间。
问题 21:Python 中的是什么@property?
这@property是一个装饰器。在 Python 中,装饰器使用户能够以相同的方式使用类(无论其属性或方法如何更改)。@property装饰器允许像访问属性一样访问函数。
问题 22:Python 中如何使用 try/except?
异常是程序执行过程中发生的错误。当此错误发生时,程序将停止并生成异常,然后对其进行处理,以防止程序崩溃。
程序产生的异常在try块中捕获,并在块中处理except。
-
Try:让您测试代码块是否存在错误。 -
Except:让您处理错误。
问题 23:解释 Python 2 和 Python 3 之间的区别
| Python 2 | Python 3 |
|---|---|
| Python 2 的字符串编码 将字符串存储为 ASCII 码。Unicode 是 ASCII 的超集,因此可以编码更多字符,包括外来字符。 |
字符串编码 Python 3 默认将字符串存储为 Unicode。 |
| Python 2除法 将 floor 函数应用于小数输出并返回一个整数。因此,5 除以 2 将返回 floor(2.5) = 2。 |
Python 3 中的除法 会返回预期的输出,即使它是小数。 |
| 打印 Python 2 不需要括号。 |
打印 Python 2 和 3 中打印语句的语法不同。Python 3 要求用括号将要打印的内容括起来。 |
| 库 许多较旧的库都是专门为 Python 2 构建的,并且不“向前兼容”。 |
库 一些较新的库是专门为 Python 3 构建的,不适用于 Python 2。 |
Python 2 在软件领域已经根深蒂固,以至于多个软件之间的相互依赖使得转变几乎不可能。
问题 24:python 中的 join 方法是什么?
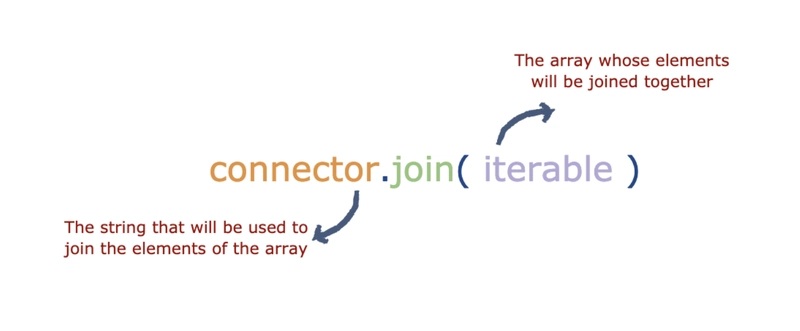
Python 中的方法join采用可迭代数据结构的元素,并使用特定的字符串连接器值将它们连接在一起。
怎么join運作?
Python 中的 join 方法是一种字符串方法,它使用特定的字符串作为连接器来连接字符串可迭代结构的元素,该结构也包含字符串或字符(数组、列表等)。
示例:使用空字符串连接元素
这将使用每个元素之间的空字符串来连接数组中的元素。
array = ['H','E','L','L','O']
connector = ""
joined_string = connector.join(array)
print(joined_string)
输出:
HELLO
问题 25:什么是词典理解?
字典推导式是在 Python 中创建字典的一种方法。它通过合并两组列表或数组形式的数据来创建字典。
其中一个列表/数组的数据将作为字典的键,而另一个列表/数组的数据将作为值。每个键都作为每个值的唯一标识符,因此两个列表/数组的大小应该相同。
这里我们来看看简单的合并:
简单合并是指对两个列表进行合并或组合,没有任何限制。换句话说,它是无条件合并。
一般语法如下:
例子
以下示例针对学院的数据库运行,并使用简单的合并操作。假设有一所学院的数据库存储了大量数据,例如学生的地址、成绩、科目、费用、学号等等。现在我们需要唯一地标识每个学生,并创建一个仅存储所有学生的新字典。我们的决策仅取决于两个问题:
- 关键应该是什么?
- 值应该是多少?
这里我们选择学号作为键,姓名作为值,因为学号是唯一的,而姓名可能会重复。所以,Alex 的学号是 122,所以元组的形式应该是 122: Alex。如果您尝试下面附带的代码,就能更好地理解这一点。
rollNumbers =[122,233,353,456]
names = ['alex','bob','can', 'don']
NewDictionary={ i:j for (i,j) in zip (rollNumbers,names)}
print(NewDictionary)
输出:
{456:'don',233:'bob',122:'alex',353:'can'}
问题 26:如何在 Python 中进行深层复制?
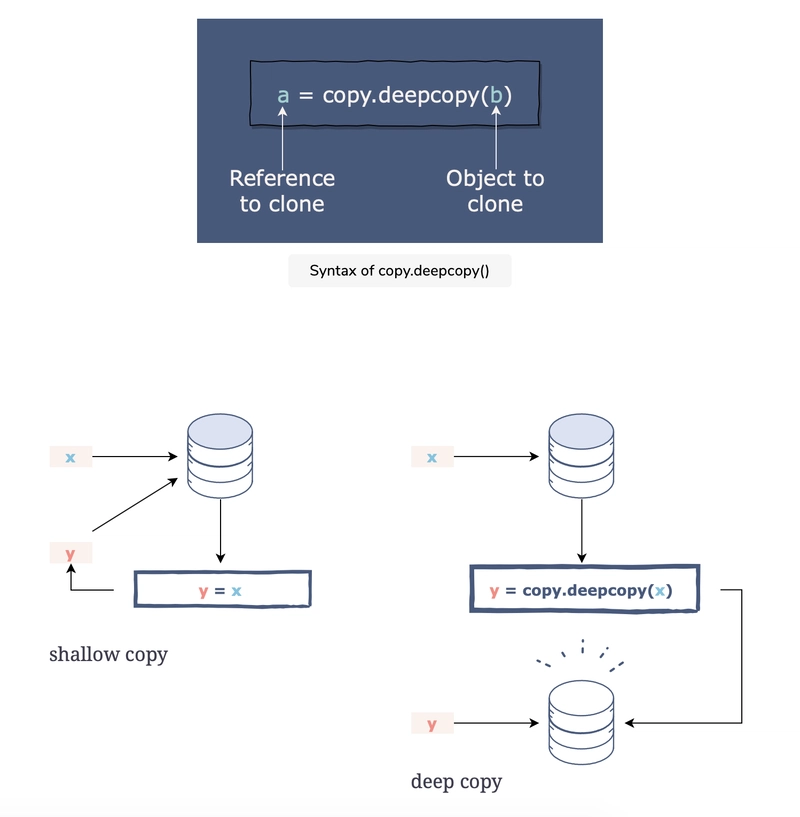
深拷贝指的是克隆一个对象。当我们使用 = 运算符时,我们并不是在克隆对象;而是将变量引用到同一个对象(又称浅拷贝)。
这意味着更改一个变量的值会影响另一个变量的值,因为它们引用(或指向)同一个对象。浅拷贝和深拷贝之间的区别仅适用于包含其他对象的对象,例如列表和类的实例。
方法
要对对象进行深层复制(或克隆),我们需要导入copyPython 内置模块。该模块提供了deepcopy()简化我们任务的方法。
句法
该函数将我们想要克隆的对象作为其唯一参数并返回该克隆。
import copy
# Using '=' operator
x = [1, 2, 3]
y = x
x[0] = 5 # value of 'y' also changes as it is the SAME object
x[1] = 15
print "Shallow copy: ", y
# Using copy.deepcopy()
a = [10, 20, 30]
b = copy.deepcopy(a)
a[1] = 70 # value of 'b' does NOT change because it is ANOTHER object
print "Deep copy: ", b
输出:
浅拷贝:[5, 15, 3]
深拷贝:[10, 20, 30]
问题 27:如何检查 Python 字典中是否存在某个键?
在提取键的值之前,检查该键是否存在于字典中是一种安全的做法。为此,Python 提供了两个内置函数:
has_key()
has_key如果字典中存在给定的键,则该方法返回 true;否则,返回 false。
Fruits = {'a': "Apple", 'b':"Banana", 'c':"Carrot"}
key_to_lookup = 'a'
if Fruits.has_key(key_to_lookup):
print "Key exists"
else:
print "Key does not exist"
输出:密钥存在
if-in陈述
该方法使用if-in语句来检查字典中是否存在给定的键。
Fruits = {'a': "Apple", 'b':"Banana", 'c':"Carrot"}
key_to_lookup = 'a'
if key_to_lookup in Fruits:
print "Key exists"
else:
print "Key does not exist"
输出:密钥存在
问题 28:如何在 Python 中实现记忆化?
考虑这个计算量很大的代码:
# Fibonacci Numbers
def fib(num):
if num == 0:
return 0
elif num == 1:
return 1
return fib(num - 1) + fib(n - 2)
可以通过 Python 装饰器实现记忆
这是完整的实现。
import timeit
def memoize_fib(func):
cache = {}
def inner(arg):
if arg not in cache:
cache[arg] = func(arg)
return cache[arg]
return inner
def fib(num):
if num == 0:
return 0
elif num == 1:
return 1
else:
return fib(num-1) + fib(num-2)
fib = memoize_fib(fib)
print(timeit.timeit('fib(30)', globals=globals(), number=1))
print(timeit.timeit('fib(30)', globals=globals(), number=1))
print(timeit.timeit('fib(30)', globals=globals(), number=1))
输出:
4.9035000301955733e-05
1.374000021314714e-06
1.2790005712304264e-06
问题 29:如何在 Python 中对字典进行排序?
我们可以按键或值对这种类型的数据进行排序,这可以通过使用 sorted() 函数来完成。
首先,我们需要知道如何从字典中检索数据并传递给此函数。
从字典中获取数据有两种基本方法:
Dictionary.keys() :仅返回任意顺序的键。Dictionary.values
() :返回值列表。Dictionary.items
() :以键值对列表的形式返回所有数据。
Sorted() 语法
此方法接受一个强制参数和两个可选参数:
数据(必填):需要排序的数据。我们将使用上述方法之一传递检索到的数据。
键(可选):我们希望基于该函数(或条件)对列表进行排序。例如,条件可以是基于字符串长度的排序,也可以是任何其他任意函数。此函数将应用于列表的每个元素,并对结果数据进行排序。如果将其留空,则将基于列表的原始值进行排序。
反向(可选):将第三个参数设置为 true 将按降序对列表进行排序。留空则按升序排序。
keys()
dict = {}
dict['1'] = 'apple'
dict['3'] = 'orange'
dict['2'] = 'pango'
lst = dict.keys()
# Sorted by key
print("Sorted by key: ", sorted(lst))
values()
dict = {}
dict['1'] = 'apple'
dict['3'] = 'orange'
dict['2'] = 'pango'
lst = dict.values()
#Sorted by value
print("Sorted by value: ", sorted(lst))
items()
dict = {}
dict['1'] = 'apple'
dict['3'] = 'orange'
dict['2'] = 'strawberry'
lst = dict.items()
# Sorted by key
print("Sorted by key: ", sorted(lst, key = lambda x : x[0]))
#Sorted by value
print("Sorted by value: ", sorted(lst, key = lambda x : x[1]))
问题 30:如何以及何时使用any()and all()?
什么是any()?
any()是一个函数,它接受一个可迭代对象(例如列表、元组、集合等),True如果其中任何一个元素的计算结果为 则返回,但如果所有元素的计算结果为True则返回。FalseFalse
传递一个可迭代对象来any()检查是否有任何元素True可以像这样完成:
one_truth = [True, False, False]
three_lies = [0, '', None]
print(any(one_truth))
print(any(three_lies))
输出:
真
假
第一个打印语句会打印,True因为 中的一个元素one_truth是True。
另一方面,第二个打印语句会打印,False因为没有元素是True,即所有元素都是False。
any()当您需要检查一系列条件时使用or。
什么是all()?
all()是另一个 Python 函数,它接受一个可迭代对象,True如果所有元素的计算结果为则返回,否则True返回。False
类似于any(),all()接受列表、元组、集合或任何可迭代对象,如下所示:
all_true = [True, 1, 'a', object()]
one_true = [True, False, False, 0]
all_false = [None, '', False, 0]
print(all(all_true))
print(all(one_true))
print(all(all_false))
输出:
真
假
假
第一个函数调用返回,True因为all_true填充了真值。
传递one_true到all()返回,False因为列表包含一个或多个虚假值。
最后,传递all_false给all()返回False,因为它还包含一个或多个虚假值。
all()当您需要检查一系列条件时使用and。
问题 31:什么是 Python Docstring?
Python 文档字符串提供了一种将文档与以下内容关联的合适方法:
- Python 模块
- Python 函数
- Python 类
它是已编写代码的指定文档。与传统的代码注释不同,代码注释应该描述函数的功能,而不是其工作原理。
可以使用以下方式访问文档字符串
__doc__对象的方法help功能
例子
def Examplefunc(str): #function that outputs the str parameter
print "The value is", str
#no return statement needed in this function
def Multiply(x,y): #function that computes the product of x and y
return x*y #returning the product of x and y
#Calling the functions
Examplefunc(9) #9 passed as the parameter)
answer = Multiply(4,2) #4 and 2 passed as the parameters
print "The product of x and y is:",answer
输出:
值为 9
x 和 y 的乘积为:8
解释
上面的函数Examplefunc接受一个变量str作为参数,然后打印该值。由于它只打印该值,因此不需要返回命令。
该函数Multiply接受两个参数x和y。然后计算乘积并使用return语句返回答案。
问题 33:解释 Python 中生成器和迭代器之间的区别。
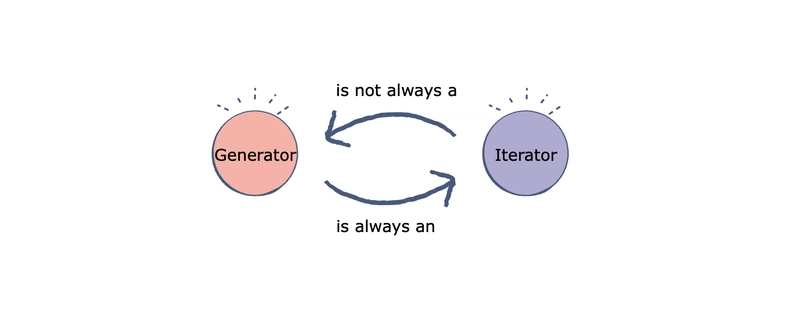
Python 中的迭代器充当对象的持有者,以便可以对其进行迭代;生成器有助于创建自定义迭代器。
除了明显的语法差异外,还有以下一些值得注意的差异:
| 发电机 | 迭代器 |
|---|---|
| 使用函数实现。 | 使用类来实现。 |
使用yield关键字。 |
不使用yield关键字。 |
| 使用结果为简洁的代码。 | 使用会导致代码相对不太简洁。 |
存储了语句之前的所有局部变量yield。 |
没有使用局部变量。 |
迭代器的实现
# Function to generate all the non-negative numbers
# up to the given non-negative number.
class UpTo:
# giving the parameter a default value of 0
def __init__(self, max = 0):
self.max = max
def __iter__(self):
self.n = 0
return self
def __next__(self):
# The next method will throw an
# exception when the termination condition is reached.
if self.n > self.max:
raise StopIteration
else:
result = self.n
self.n += 1
return result
for number in UpTo(5):
print(number)
输出:
0
1
2
3
4
5
Generator 的实现
# Function to generate all the non-negative numbers
# up to the given non-negative number
def upto(n):
for i in range(n+1):
# The yield statement is what makes a function
# a generator
yield i
for number in upto(5):
print(number)
输出:
0
1
2
3
4
5
问题 34:defaultdictPython 中有什么?
Python 字典dict包含单词及其含义,以及任意数据类型的键值对。defaultdict是内置dict类的另一个分支。
有何defaultdict不同?
是类defaultdict的一个分支dict。它的重要性在于它允许根据正在创建的字典类型为每个新键赋予一个默认值。
可以通过给出其声明来创建,该声明包含一个defaultdict可以具有三个值的参数:列表、集合或整数。根据指定的数据类型,将创建字典,并且当defaultdict添加或访问字典中不存在的任何键时,将为其分配一个默认值,而不是赋值KeyError。
例子
下面的第一个代码片段展示了一个简单的字典,以及当访问字典中不存在的键时如何出现错误。
dict_demo = dict()
print(dict_demo[3])
现在让我们引入adefaultdict并看看会发生什么。
from collections import defaultdict
defaultdict_demo = defaultdict(int)
print(defaultdict_demo[3])
输出: 0
在本例中,我们将 int 作为数据类型传递给了defaultdict。因此,任何 中不存在的键都defaultdict_demo将被赋值为 0,除非为其定义了值。
注意:您也可以将
set或list作为参数
问题 35:什么是 Python 模块?
Python 模块是一个 Python 文件,包含一组在应用程序中使用的函数和变量。变量可以是任何类型(数组、字典、对象等)。
模块可以是:
-
内置
-
用户定义
Python 模块的好处
在 Python 中创建和使用模块有几个主要好处:
-
结构化代码
- 代码被分组到一个 Python 文件中,从而进行逻辑组织,使开发更容易且不易出错。
- 代码更易于理解和使用。
-
可重用性
- 单个模块中定义的功能可以轻松地被应用程序的其他部分重用。这样就无需重新创建重复的代码。
Python 面试问题 - 编码
在本节中,我们将探讨与列表、链表、图、树、多线程/并发等相关的常见编程面试问题。让我们深入探讨。
问题 36:在 Python 中反转字符串
让我们使用切片方法反转字符串“Python”。
要反转字符串,我们只需创建一个以字符串长度开始并以索引 0 结束的切片。
要使用切片来反转字符串,请写入:
stringname[stringlength::-1] # method 1
或者不指定字符串的长度:
stringname[::-1] # method2
slice 语句的意思是,从字符串长度开始,到位置 0 结束,以步长 -1(或向后一步)移动。
str="Python" # initial string
stringlength=len(str) # calculate length of the list
slicedString=str[stringlength::-1] # slicing
print (slicedString) # print the reversed string
输出: nohtyP
这只是 Python 中反转字符串的一种方法。另外两个值得注意的方法是 Loop 和 Use Join。
问题 37:检查 Python 字符串是否包含另一个字符串
有几种方法可以检查这一点。在本文中,我们将讨论其中find一种方法。
该find方法检查字符串是否包含子字符串。如果包含,则返回子字符串在字符串中的起始索引;否则,返回 -1。
一般语法是:
string.find(substring)
a_string="Python Programming"
substring1="Programming"
substring2="Language"
print("Check if "+a_string+" contains "+substring1+":")
print(a_string.find(substring1))
print("Check if "+a_string+" contains "+substring2+":")
print(a_string.find(substring2))
输出:
检查 Python 编程是否包含编程:7
检查 Python 编程是否包含语言:-1
检查一个字符串是否包含另一个字符串的另外两种值得注意的方法是使用in运算符或使用count方法。
问题 38:在 Python 中实现广度优先搜索(BFS)
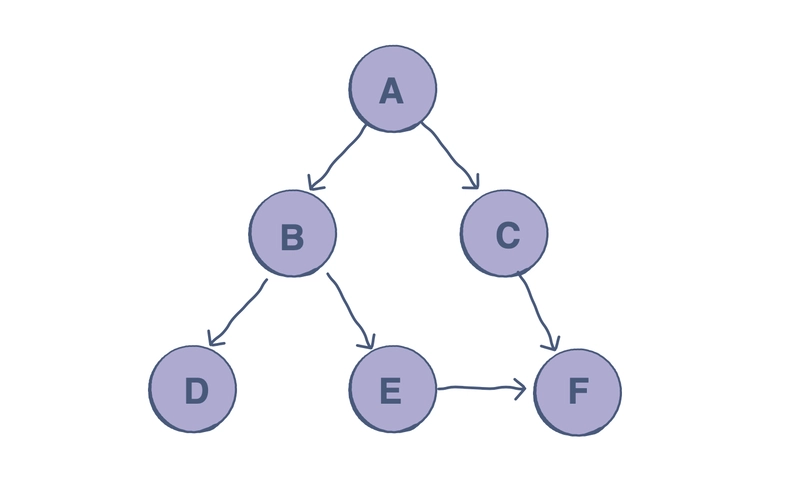
考虑以下代码中实现的图表:
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : ['F'],
'D' : [],
'E' : ['F'],
'F' : []
}
visited = [] # List to keep track of visited nodes.
queue = [] #Initialize a queue
def bfs(visited, graph, node):
visited.append(node)
queue.append(node)
while queue:
s = queue.pop(0)
print (s, end = " ")
for neighbour in graph[s]:
if neighbour not in visited:
visited.append(neighbour)
queue.append(neighbour)
# Driver Code
bfs(visited, graph, 'A')
输出: ABCDEF
解释
第 3-10 行:图示中的图使用邻接表表示。在 Python 中,一种简单的方法是使用字典数据结构,其中每个顶点都存储了其相邻节点的列表。
第 12 行: visited是用于跟踪已访问节点的列表。
第 13 行: queue是用于跟踪当前队列中的节点的列表。
第 29 行:该函数的参数bfs是visited列表、graph字典形式的和起始节点A。
第 15-26 行: bfs 遵循上面描述的算法:
- 它检查并将起始节点附加到
visited列表和queue。 - 然后,当队列包含元素时,它会不断从队列中取出节点,如果该节点的邻居未被访问,则将其附加到队列中,并将它们标记为已访问。
- 这会持续直到队列为空。
时间复杂度
由于所有节点和顶点都被访问,图上 BFS 的时间复杂度为 O(V + E);其中 V 是顶点数,E 是边数。
问题 39:在 Python 中实现深度优先搜索(DFS)
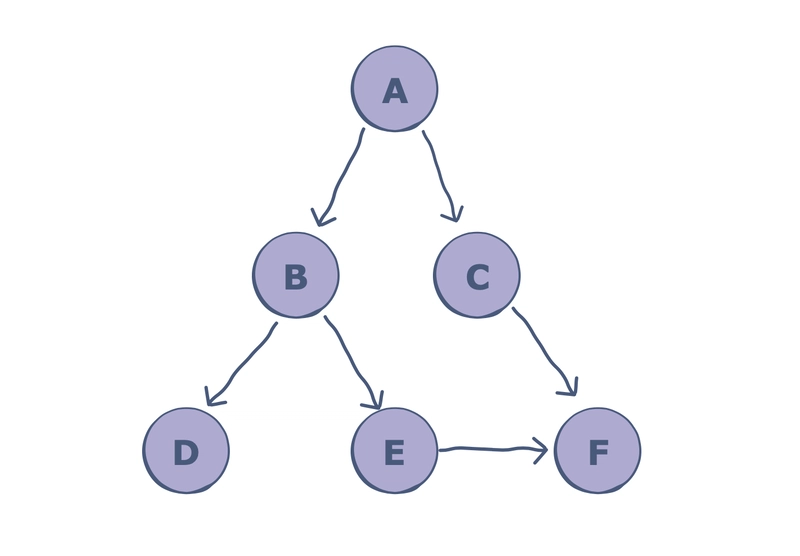
考虑一下这个图表,在下面的代码中实现:
# Using a Python dictionary to act as an adjacency list
graph = {
'A' : ['B','C'],
'B' : ['D', 'E'],
'C' : ['F'],
'D' : [],
'E' : ['F'],
'F' : []
}
visited = set() # Set to keep track of visited nodes.
def dfs(visited, graph, node):
if node not in visited:
print (node)
visited.add(node)
for neighbour in graph[node]:
dfs(visited, graph, neighbour)
# Driver Code
dfs(visited, graph, 'A')
输出: ABDEFC
解释
第 2-9 行:图示中的图使用邻接表表示——在 Python 中,一种简单的方法是使用字典数据结构。每个顶点都存储了其相邻节点的列表。
第 11 行: visited是用于跟踪已访问节点的集合。
第 21 行:dfs调用该函数并传递visited集合、graph以字典形式存在的 以及A,这是起始节点。
第 13-18 行: dfs遵循上面描述的算法:
- 它首先检查当前节点是否未被访问 - 如果是,则将其附加到
visited集合中。 - 然后对于当前节点的每个邻居,
dfs再次调用该函数。 - 当所有节点都被访问后,调用基准情况。然后函数返回。
时间复杂度
由于所有节点和顶点都会被访问,因此图上的 DFS 的平均时间复杂度为 O(V + E),其中 V 是顶点数,E 是边数。对于树上的 DFS,时间复杂度为 O(V),其中 V 是节点数。
继续学习。
练习最常见的 Python 面试题,提升你的自信心。Educative 的文本课程易于浏览,并提供实时浏览器编程环境,让学习更快速、更高效。
问题 40:在 Python 中实现通配符
在 Python 中,您可以使用 regex(正则表达式)库实现通配符。
点.符号代替了问号?符号。因此,要搜索所有与颜色模式匹配的单词,代码如下所示。
# Regular expression library
import re
# Add or remove the words in this list to vary the results
wordlist = ["color", "colour", "work", "working",
"fox", "worker", "working"]
for word in wordlist:
# The . symbol is used in place of ? symbol
if re.search('col.r', word) :
print (word)
输出:彩色
问题 41:在 Python 中实现合并排序
以下是 Python 中合并排序的代码:
def mergeSort(myList):
if len(myList) > 1:
mid = len(myList) // 2
left = myList[:mid]
right = myList[mid:]
# Recursive call on each half
mergeSort(left)
mergeSort(right)
# Two iterators for traversing the two halves
i = 0
j = 0
# Iterator for the main list
k = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
# The value from the left half has been used
myList[k] = left[i]
# Move the iterator forward
i += 1
else:
myList[k] = right[j]
j += 1
# Move to the next slot
k += 1
# For all the remaining values
while i < len(left):
myList[k] = left[i]
i += 1
k += 1
while j < len(right):
myList[k]=right[j]
j += 1
k += 1
myList = [54,26,93,17,77,31,44,55,20]
mergeSort(myList)
print(myList)
输出: [17, 20, 26, 31, 44, 54, 55, 77, 93]
解释
这是实现合并排序的递归方法。通过此方法获取排序数组所需的步骤如下:
-
在每次递归调用中,列表被分成和
left,right直到获得两个相邻的元素。 -
现在开始排序过程。每次调用
i和j迭代器都会遍历列表的两部分。k迭代器会遍历整个列表,并在此过程中进行更改。 -
如果 处的值
i小于 处的值j,left[i]则 被赋值给myList[k]槽位并i递增。如果不是,则right[j]选择 。 -
这样,所分配的值
k就全部排序了。 -
在这个循环的最后,其中一半可能还没有被完全遍历。它的值会被简单地赋给列表中剩余的槽位。
时间复杂度
该算法的复杂度为 O(n.logn)。这是因为列表拆分需要 log(n) 次调用,而合并过程在每次调用中都需要线性时间。
问题 42:用 Python 实现 Dijkstra 算法
基本算法
- 从每个未访问的顶点中,选择距离最小的顶点并访问它。
- 更新所访问顶点的每个相邻顶点的距离,其当前距离大于其总和以及它们之间的边的权重。
- 重复步骤 1 和 2,直到所有顶点都被访问。
以下是具体实现
import sys
# Function to find out which of the unvisited node
# needs to be visited next
def to_be_visited():
global visited_and_distance
v = -10
# Choosing the vertex with the minimum distance
for index in range(number_of_vertices):
if visited_and_distance[index][0] == 0 \
and (v < 0 or visited_and_distance[index][1] <= \
visited_and_distance[v][1]):
v = index
return v
# Creating the graph as an adjacency matrix
vertices = [[0, 1, 1, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
[0, 0, 0, 0]]
edges = [[0, 3, 4, 0],
[0, 0, 0.5, 0],
[0, 0, 0, 1],
[0, 0, 0, 0]]
number_of_vertices = len(vertices[0])
# The first element of the lists inside visited_and_distance
# denotes if the vertex has been visited.
# The second element of the lists inside the visited_and_distance
# denotes the distance from the source.
visited_and_distance = [[0, 0]]
for i in range(number_of_vertices-1):
visited_and_distance.append([0, sys.maxsize])
for vertex in range(number_of_vertices):
# Finding the next vertex to be visited.
to_visit = to_be_visited()
for neighbor_index in range(number_of_vertices):
# Calculating the new distance for all unvisited neighbours
# of the chosen vertex.
if vertices[to_visit][neighbor_index] == 1 and \
visited_and_distance[neighbor_index][0] == 0:
new_distance = visited_and_distance[to_visit][1] \
+ edges[to_visit][neighbor_index]
# Updating the distance of the neighbor if its current distance
# is greater than the distance that has just been calculated
if visited_and_distance[neighbor_index][1] > new_distance:
visited_and_distance[neighbor_index][1] = new_distance
# Visiting the vertex found earlier
visited_and_distance[to_visit][0] = 1
i = 0
# Printing out the shortest distance from the source to each vertex
for distance in visited_and_distance:
print("The shortest distance of ",chr(ord('a') + i),\
" from the source vertex a is:",distance[1])
i = i + 1
输出:
a 到源顶点 a 的最短距离为:0
b 到源顶点 a 的最短距离为:3
c 到源顶点 a 的最短距离为:3.5
d 到源顶点 a 的最短距离为:4.5
问题 43:合并两个排序列表
# Merge list1 and list2 and return resulted list
def merge_lists(lst1, lst2):
index_arr1 = 0
index_arr2 = 0
index_result = 0
result = []
for i in range(len(lst1)+len(lst2)):
result.append(i)
# Traverse Both lists and insert smaller value from arr1 or arr2
# into result list and then increment that lists index.
# If a list is completely traversed, while other one is left then just
# copy all the remaining elements into result list
while (index_arr1 < len(lst1)) and (index_arr2 < len(lst2)):
if (lst1[index_arr1] < lst2[index_arr2]):
result[index_result] = lst1[index_arr1]
index_result += 1
index_arr1 += 1
else:
result[index_result] = lst2[index_arr2]
index_result += 1
index_arr2 += 1
while (index_arr1 < len(lst1)):
result[index_result] = lst1[index_arr1]
index_result += 1
index_arr1 += 1
while (index_arr2 < len(lst2)):
result[index_result] = lst2[index_arr2]
index_result += 1
index_arr2 += 1
return result
print(merge_lists([4, 5, 6], [-2, -1, 0, 7]))
输出: [-2, -1, 0, 4, 5, 6, 7]
上面的解决方案是解决这个问题的更直观的方法。
-
首先创建一个新的空列表。该列表将按排序顺序填充两个列表的所有元素并返回。
-
然后将三个变量初始化为零,以存储每个列表的当前索引。
-
然后比较两个给定列表的当前索引处的元素,将较小的列表附加到新列表,并将该列表的索引增加 1。
-
重复此操作,直到到达其中一个列表的末尾,并将另一个列表附加到合并列表中。
时间复杂度:
该算法的时间复杂度为 O(n+m),其中 nn 和 mm 是列表的长度。这是因为两个列表都至少迭代一次。
请注意,这个问题也可以通过就地合并来解决。
问题 44:找出两个加起来等于 'k' 的数字
def binarySearch(a, item, curr):
first = 0
last = len(a) - 1
found = False
index = -1
while first <= last and not found:
mid = (first + last) // 2
if a[mid] == item:
index = mid
found = True
else:
if item < a[mid]:
last = mid - 1
else:
first = mid + 1
if found:
return index
else:
return -1
def findSum(lst, k):
lst.sort()
for j in range(len(lst)):
# find the difference in list through binary search
# return the only if we find an index
index = binarySearch(lst, k -lst[j], j)
if index is not -1 and index is not j:
return [lst[j], k -lst[j]]
print(findSum([1, 5, 3], 2))
print(findSum([1, 2, 3, 4], 5))
输出:
无
[1,4]
解决这个问题的方法是先对列表进行排序。然后,对列表中的每个元素,使用二分查找法查找该元素与预期和之间的差值。换句话说,如果预期和为,k而排序后列表的第一个元素为
我们将进行二分查找
重复搜索,直到找到为止。您可以binarySearch()按照自己喜欢的方式实现该函数,递归或迭代均可。
时间复杂度
由于大多数基于比较的最优排序函数的时间复杂度为 O(nlogn),我们假设 Python.sort()函数的时间复杂度也相同。此外,二分查找查找单个元素的时间复杂度为 O(logn),因此对所有 n 个元素进行二分查找的时间复杂度为 O(nlogn)。
问题 45:查找列表中第一个不重复的整数
这里您可以使用 Python 字典来记录重复次数。
示例输入:
[9,2,3,2,6,6]
def findFirstUnique(lst):
counts = {} # Creating a dictionary
# Initializing dictionary with pairs like (lst[i],(count,order))
counts = counts.fromkeys(lst, (0,len(lst)))
order = 0
for ele in lst:
# counts[ele][0] += 1 # Incrementing for every repitition
# counts[ele][1] = order
counts[ele] = (counts[ele][0]+1 , order)
order += 1 # increment order
answer = None
answer_key = None
# filter non-repeating with least order
for ele in lst:
if (counts[ele][0] is 1) and (answer is None):
answer = counts[ele]
answer_key = ele
elif answer is None:
continue
elif (counts[ele][0] is 1) and (counts[ele][1] < answer[1]):
answer = counts[ele]
answer_key = ele
return answer_key
print(findFirstUnique([1, 1, 1, 2]))
输出: 2
字典中的键counts是给定列表的元素,值是每个元素在列表中出现的次数。我们在第 23 行返回列表中最多出现一次的元素。我们需要维护元组值中每个键的更新顺序。
时间复杂度
由于列表仅迭代两次,并且counts字典以线性时间复杂度初始化,因此该解决方案的时间复杂度是线性的,即 O(n)。
问题 46:找出链表的中间值
要查看实际的代码解决方案,请转到原始帖子。
这里你可以使用两个同时工作的指针。可以这样想:
- 快速指针每次移动两步,直到列表末尾
- 慢指针每次移动一步
- 当快指针到达末尾时,慢指针将位于中间
使用该算法,可以加快进程,因为长度的计算和遍历直到中间是同时进行的。
时间复杂度
你以两倍的速度遍历链表,所以速度肯定更快了。然而,瓶颈复杂度仍然是 O(n)。
问题 47:反转队列的前 ‘k’ 个元素
要查看实际的代码解决方案,请转到原始帖子
解释
检查输入是否无效,例如,在第2行检查队列是否为空、是否k大于队列、是否k为负。如果输入有效,则首先创建一个堆栈。可用的堆栈函数如下:
- 构造函数:
myStack() - 推送元素:
push(int)将元素添加到堆栈中。 - 弹出元素:
pop()从堆栈中移除或弹出顶部元素。 - 检查是否为空:
isEmpty()如果堆栈为空则返回 true,否则返回 false。 - 返回:
back()返回最后添加的元素,而不将其从堆栈中移除。 - 返回前端:
front()返回顶部元素(已在开始时添加)而不将其从堆栈中移除。
我们的函数reverseK(queue, k)将队列作为输入参数。k表示我们要反转的元素数量。可用的队列函数包括:
-
构造函数:
myQueue(size)size 应该是一个指定队列大小的整数。 -
入队:
enqueue(int) -
出队:
dequeue() -
检查是否为空:
isEmpty() -
检查尺寸:
size()
现在,转到实际逻辑,k从队列前面出队第一个元素,并将它们推送到我们之前stack.push(queue.dequeue())在第 8 行创建的堆栈中。
k所有值都入栈后,开始弹出它们并按顺序将它们放入队列的尾部。我们将queue.enqueue(stack.pop())在第 12 行执行此操作。此步骤完成后,我们将得到一个空栈,k反转后的元素将被添加到队列的尾部。
现在我们需要将这些反转的元素移到队列的前面。为此,我们queue.enqueue(queue.dequeue())在第 16 行使用了以下代码:首先从队列的后面出队
问题 48:求二叉搜索树(BST)的高度
这里可以使用递归来找到左子树和右子树的高度。
要查看实际的代码解决方案,请访问原始帖子。
解释
这里,如果给定节点为 None,则返回 -1。然后,在左右子树上调用 findHeight() 函数,并返回值较大的那个节点,该值加 1。如果给定节点为 None,则不会返回 0,因为叶节点的高度为 0。
时间复杂度
代码的时间复杂度为 O(n)O(n),因为必须遍历整棵树的所有节点。
问题 49:将最大堆转换为最小堆
这里我们将对所有父节点进行最小堆化。
def minHeapify(heap, index):
left = index * 2 + 1
right = (index * 2) + 2
smallest = index
# check if left child exists and is less than smallest
if len(heap) > left and heap[smallest] > heap[left]:
smallest = left
# check if right child exists and is less than smallest
if len(heap) > right and heap[smallest] > heap[right]:
smallest = right
# check if current index is not the smallest
if smallest != index:
# swap current index value with smallest
tmp = heap[smallest]
heap[smallest] = heap[index]
heap[index] = tmp
# minHeapify the new node
minHeapify(heap, smallest)
return heap
def convertMax(maxHeap):
# iterate from middle to first element
# middle to first indices contain all parent nodes
for i in range((len(maxHeap))//2, -1, -1):
# call minHeapify on all parent nodes
maxHeap = minHeapify(maxHeap, i)
return maxHeap
maxHeap = [9, 4, 7, 1, -2, 6, 5]
print(convertMax(maxHeap))
输出: [-2, 1, 5, 9, 4, 6, 7]
解释
记住,我们可以将给定元素maxHeap视为一个常规元素列表,并对其进行重新排序,使其准确地表示最小堆。我们在这个解决方案中正是这样做的。该convertMax()函数通过在每个节点上调用该函数,从最低父节点开始恢复所有节点的堆属性minHeapify()。
时间复杂度:
该minHeapify()函数针对堆中一半的节点进行调用。该minHeapify()函数耗时 O(log(n)),调用时间为
节点,因此该解决方案需要 O(nlog(n)) 时间。
问题 50:检测链表中的循环
要查看实际的代码解决方案,请访问原始帖子。
解释
遍历整个链表,并将每个访问过的节点添加到visited_nodes集合中。在每个节点处,我们检查它是否已被访问过。
原则上,如果一个节点被重新访问,则存在一个循环!
时间复杂度
我们对列表进行一次迭代。平均而言,在集合中查找需要 O(1) 的时间。因此,该算法的平均运行时间为 O(n)。然而,在最坏的情况下,查找时间可能会增加到 O(n),这将导致算法在
不要停在这里
你的学习和准备才刚刚开始。练习 Python 面试中最常见的问题,将你的自信提升到一个新的高度。《深入理解编程面试:编程问题模式》已经帮助无数软件工程师做好准备,并在微软、亚马逊、谷歌等公司找到工作。
在本课程中,你将探索构成编程问题的 16 个基本模式。一旦你理解了一个模式,你就可以将其应用于数百个类似但又不同的其他问题。点击上方链接即可免费预览。
祝你好运!
其他资源
文章来源:https://dev.to/education/50-python-interview-questions-and-answers-nh2 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com