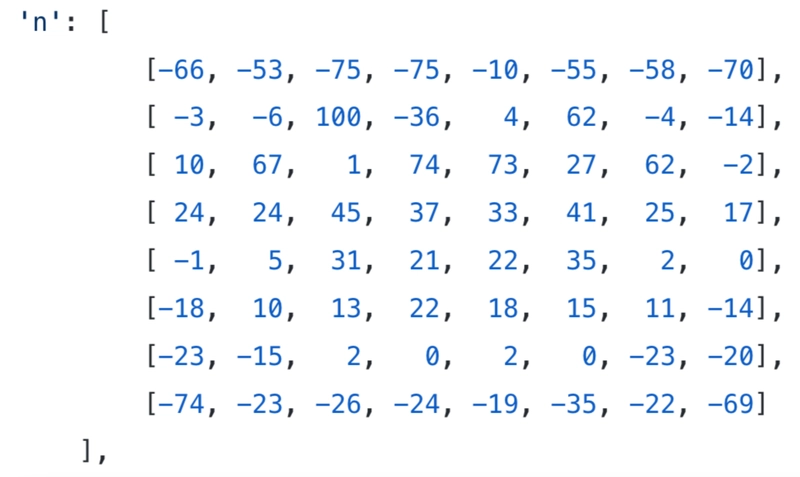后端开发教程 - Java、Spring Boot 实战 - msg200.com
使用 JavaScript 构建一个简单的国际象棋 AI
国际象棋是一项很棒的游戏。如果你擅长它，那就更好了。遗憾的是，我从来没有花时间学习国际象棋策略，所以我决定依靠计算和博弈论的力量！作为一个有趣的业余项目，我用 JavaScript 实现了一个简单的国际象棋 AI。
您可以在我的GitHub 存储库中找到本教程的完整源代码。
最终产品可以在https://zeyu2001.github.io/chess-ai/上玩。
 上玩](https://media2.dev.to/dynamic/image/width=800%2Cheight=%2Cfit=scale-down%2Cgravity=auto%2Cformat=auto/https%3A%2F%2Fcdn-images-1.medium.com%2Fmax%2F2000%2F1%2Aj9HpWMAOCHXL5HuIV6IMzg.png)
先决条件
你应该了解基本的编程知识以及树形数据结构的一般概念。其他内容将在本教程中涵盖。
涉及的两个主要算法是极小极大算法和alpha-beta 剪枝。这些将在后面深入解释，如果你有编程经验，应该相对容易掌握。
首先要做的事情……
先把 GUI 和游戏机制处理好。这样我们就能把注意力集中在应用程序最精彩的部分：决策（AI）部分！为此，我们将使用一些外部库：
-
chessboard.js处理图形界面，即棋盘本身。
-
chess.js处理游戏机制，例如移动生成/验证。
使用这些库，您应该能够按照chessboard.js网站上的示例（特别是 5000 到 5005）创建一个可以运行的国际象棋游戏。
评估函数
太棒了！我们有一个可以运行的棋盘。但是，如何实现一个能够（相当）下好棋的人工智能呢？嗯，我们需要一个评估函数。基本上，我们希望为每个棋盘实例（即棋盘上每组棋子的位置）分配一个“分数”，以便我们的人工智能能够判断哪些位置比其他位置更有利。
零和博弈
国际象棋是一场零和游戏。玩家 A 获得的任何优势都意味着玩家 B 处于劣势。优势可以表现为吃掉对手的棋子，或让棋子处于有利位置。因此，从我们的 AI 角度分配分数时，正分表示我们的 AI 总体上占优势，而对手处于劣势；负分则表示我们的 AI 总体上占劣势，而对手处于优势。
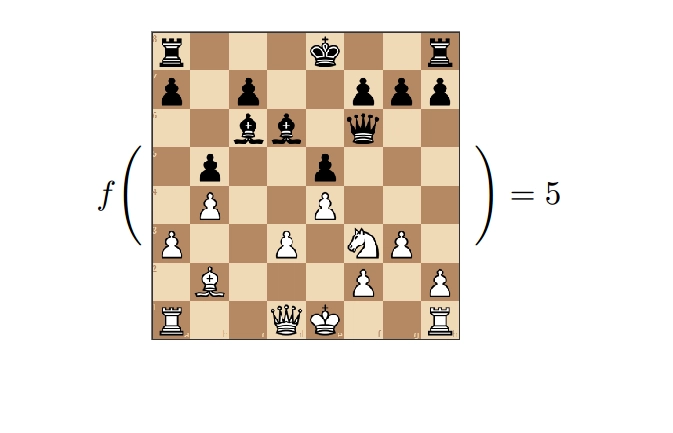
一个简单的例子
例如，起始位置的得分为 0，表示双方都尚未占据优势。游戏进行到后期，我们需要在两个步骤之间做出选择：步骤 A 还是步骤 B。假设步骤 A 吃掉一个后，我们的得分为 900；步骤 B 吃掉一个兵，我们的得分为 100。
AI 将能够比较两种可能的情况，并判定 A 步是更好的选择。当然，这并没有考虑未来的后果——如果 A 步给了对手进攻的机会怎么办？在接下来的章节中，我们将通过执行前瞻来预测后续的走法，从而克服这一障碍。
单件重量
我们评估的第一步是为每种棋子类型分配权重。如果我们的AI从黑方角度出发，任何黑棋都会增加我们的分数，而任何白棋都会减少我们的分数，具体权重如下：
-
棋子：100
-
骑士：280
-
主教：320
-
车：479
-
女王：929
-
国王：60,000
方桌
我们现在根据棋盘上棋子的位置计算得分，但有些位置比其他位置更有利。例如，机动性更高的位置应该更有利。为此，我们使用了“棋子方格表”（PST），它会根据每个棋子在棋盘上的位置为其分配额外的得分增量。
例如，骑士的 PST 鼓励向中心移动：
这是从白色的角度来看的，因此它必须反映在黑色中。
我当然不是国际象棋专家，所以棋子重量和 PST 值都改编自Sunfish.py。以下是我对评估函数的实现。请注意，我们不是每次评估都迭代 64 个方格，而是直接从 0 开始，根据最新的一步棋对分数进行加减，同时跟踪之前的分数。
| /* | |
| * Piece Square Tables, adapted from Sunfish.py: | |
| * https://github.com/thomasahle/sunfish/blob/master/sunfish.py | |
| */ | |
| var weights = { 'p': 100, 'n': 280, 'b': 320, 'r': 479, 'q': 929, 'k': 60000, 'k_e': 60000 }; | |
| var pst_w = { | |
| 'p':[ | |
| [ 100, 100, 100, 100, 105, 100, 100, 100], | |
| [ 78, 83, 86, 73, 102, 82, 85, 90], | |
| [ 7, 29, 21, 44, 40, 31, 44, 7], | |
| [ -17, 16, -2, 15, 14, 0, 15, -13], | |
| [ -26, 3, 10, 9, 6, 1, 0, -23], | |
| [ -22, 9, 5, -11, -10, -2, 3, -19], | |
| [ -31, 8, -7, -37, -36, -14, 3, -31], | |
| [ 0, 0, 0, 0, 0, 0, 0, 0] | |
| ], | |
| 'n': [ | |
| [-66, -53, -75, -75, -10, -55, -58, -70], | |
| [ -3, -6, 100, -36, 4, 62, -4, -14], | |
| [ 10, 67, 1, 74, 73, 27, 62, -2], | |
| [ 24, 24, 45, 37, 33, 41, 25, 17], | |
| [ -1, 5, 31, 21, 22, 35, 2, 0], | |
| [-18, 10, 13, 22, 18, 15, 11, -14], | |
| [-23, -15, 2, 0, 2, 0, -23, -20], | |
| [-74, -23, -26, -24, -19, -35, -22, -69] | |
| ], | |
| 'b': [ | |
| [-59, -78, -82, -76, -23,-107, -37, -50], | |
| [-11, 20, 35, -42, -39, 31, 2, -22], | |
| [ -9, 39, -32, 41, 52, -10, 28, -14], | |
| [ 25, 17, 20, 34, 26, 25, 15, 10], | |
| [ 13, 10, 17, 23, 17, 16, 0, 7], | |
| [ 14, 25, 24, 15, 8, 25, 20, 15], | |
| [ 19, 20, 11, 6, 7, 6, 20, 16], | |
| [ -7, 2, -15, -12, -14, -15, -10, -10] | |
| ], | |
| 'r': [ | |
| [ 35, 29, 33, 4, 37, 33, 56, 50], | |
| [ 55, 29, 56, 67, 55, 62, 34, 60], | |
| [ 19, 35, 28, 33, 45, 27, 25, 15], | |
| [ 0, 5, 16, 13, 18, -4, -9, -6], | |
| [-28, -35, -16, -21, -13, -29, -46, -30], | |
| [-42, -28, -42, -25, -25, -35, -26, -46], | |
| [-53, -38, -31, -26, -29, -43, -44, -53], | |
| [-30, -24, -18, 5, -2, -18, -31, -32] | |
| ], | |
| 'q': [ | |
| [ 6, 1, -8,-104, 69, 24, 88, 26], | |
| [ 14, 32, 60, -10, 20, 76, 57, 24], | |
| [ -2, 43, 32, 60, 72, 63, 43, 2], | |
| [ 1, -16, 22, 17, 25, 20, -13, -6], | |
| [-14, -15, -2, -5, -1, -10, -20, -22], | |
| [-30, -6, -13, -11, -16, -11, -16, -27], | |
| [-36, -18, 0, -19, -15, -15, -21, -38], | |
| [-39, -30, -31, -13, -31, -36, -34, -42] | |
| ], | |
| 'k': [ | |
| [ 4, 54, 47, -99, -99, 60, 83, -62], | |
| [-32, 10, 55, 56, 56, 55, 10, 3], | |
| [-62, 12, -57, 44, -67, 28, 37, -31], | |
| [-55, 50, 11, -4, -19, 13, 0, -49], | |
| [-55, -43, -52, -28, -51, -47, -8, -50], | |
| [-47, -42, -43, -79, -64, -32, -29, -32], | |
| [ -4, 3, -14, -50, -57, -18, 13, 4], | |
| [ 17, 30, -3, -14, 6, -1, 40, 18] | |
| ], | |
| // Endgame King Table | |
| 'k_e': [ | |
| [-50, -40, -30, -20, -20, -30, -40, -50], | |
| [-30, -20, -10, 0, 0, -10, -20, -30], | |
| [-30, -10, 20, 30, 30, 20, -10, -30], | |
| [-30, -10, 30, 40, 40, 30, -10, -30], | |
| [-30, -10, 30, 40, 40, 30, -10, -30], | |
| [-30, -10, 20, 30, 30, 20, -10, -30], | |
| [-30, -30, 0, 0, 0, 0, -30, -30], | |
| [-50, -30, -30, -30, -30, -30, -30, -50] | |
| ] | |
| }; | |
| var pst_b = { | |
| 'p': pst_w['p'].slice().reverse(), | |
| 'n': pst_w['n'].slice().reverse(), | |
| 'b': pst_w['b'].slice().reverse(), | |
| 'r': pst_w['r'].slice().reverse(), | |
| 'q': pst_w['q'].slice().reverse(), | |
| 'k': pst_w['k'].slice().reverse(), | |
| 'k_e': pst_w['k_e'].slice().reverse() | |
| } | |
| var pstOpponent = {'w': pst_b, 'b': pst_w}; | |
| var pstSelf = {'w': pst_w, 'b': pst_b}; | |
| /* | |
| * Evaluates the board at this point in time, | |
| * using the material weights and piece square tables. | |
| */ | |
| function evaluateBoard (move, prevSum, color) | |
| { | |
| var from = [8 - parseInt(move.from[1]), move.from.charCodeAt(0) - 'a'.charCodeAt(0)]; | |
| var to = [8 - parseInt(move.to[1]), move.to.charCodeAt(0) - 'a'.charCodeAt(0)]; | |
| // Change endgame behavior for kings | |
| if (prevSum < -1500) | |
| { | |
| if (move.piece === 'k') {move.piece = 'k_e'} | |
| else if (move.captured === 'k') {move.captured = 'k_e'} | |
| } | |
| if ('captured' in move) | |
| { | |
| // Opponent piece was captured (good for us) | |
| if (move.color === color) | |
| { | |
| prevSum += (weights[move.captured] + pstOpponent[move.color][move.captured][to[0]][to[1]]); | |
| } | |
| // Our piece was captured (bad for us) | |
| else | |
| { | |
| prevSum -= (weights[move.captured] + pstSelf[move.color][move.captured][to[0]][to[1]]); | |
| } | |
| } | |
| if (move.flags.includes('p')) | |
| { | |
| // NOTE: promote to queen for simplicity | |
| move.promotion = 'q'; | |
| // Our piece was promoted (good for us) | |
| if (move.color === color) | |
| { | |
| prevSum -= (weights[move.piece] + pstSelf[move.color][move.piece][from[0]][from[1]]); | |
| prevSum += (weights[move.promotion] + pstSelf[move.color][move.promotion][to[0]][to[1]]); | |
| } | |
| // Opponent piece was promoted (bad for us) | |
| else | |
| { | |
| prevSum += (weights[move.piece] + pstSelf[move.color][move.piece][from[0]][from[1]]); | |
| prevSum -= (weights[move.promotion] + pstSelf[move.color][move.promotion][to[0]][to[1]]); | |
| } | |
| } | |
| else | |
| { | |
| // The moved piece still exists on the updated board, so we only need to update the position value | |
| if (move.color !== color) | |
| { | |
| prevSum += pstSelf[move.color][move.piece][from[0]][from[1]]; | |
| prevSum -= pstSelf[move.color][move.piece][to[0]][to[1]]; | |
| } | |
| else | |
| { | |
| prevSum -= pstSelf[move.color][move.piece][from[0]][from[1]]; | |
| prevSum += pstSelf[move.color][move.piece][to[0]][to[1]]; | |
| } | |
| } | |
| return prevSum; | |
| } |
极小极大值
现在我们有了评估算法，可以开始做出明智的决策了！我们将使用极小极大算法，我强烈建议您阅读维基百科文章，以便更好地理解这一决策策略。
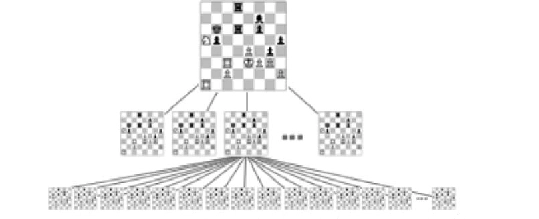
博弈树
我们可以将棋盘位置表示为*游戏树*中的节点。每个节点都是一个棋盘实例，并且具有与可从父节点采取的可能走法相对应的子节点。
尽量减少损失
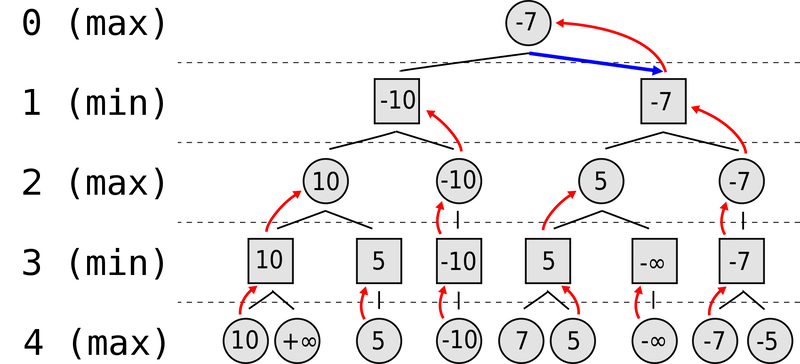
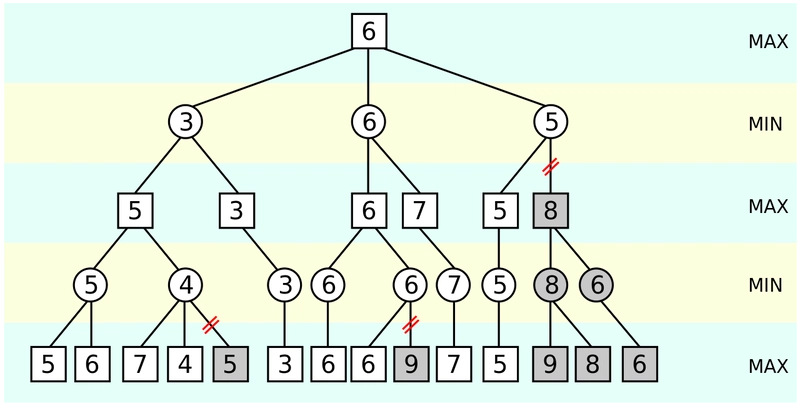
本质上，极小化最大化的目标是最小化可能的损失，前提是假设双方都是理性的决策者。我们可以将可能的行动表示为一棵博弈树，其中每一层都在最大化和最小化的玩家之间交替。我们是最大化玩家，试图最大化我们的分数；而对手是最小化玩家，试图最小化我们的分数。
在叶节点处，对评估得分进行回溯。正无穷和负无穷分别表示胜利和失败。在每个递归层中，最大化和最小化的角色交替进行。第 0 层是当前游戏状态，目标是最大化我们的得分。
替代动作
我们的人工智能必须回答的问题是：“在第 0 层的所有可能动作中，哪个动作可以保证获得最高分？”
这就好比问：“假设我的对手总是做出最优决策，那么哪种举动最有可能获得最佳得分？”
如果我们希望我们的人工智能在国际象棋方面有所建树，就必须进行“向前看”来预测对手的后续动作。当然，我们只能提前预测几轮——从计算上来说，预测最终的胜负状态是不可行的。我们必须引入一个深度限制，该限制对应于我们愿意向前看的轮数，并在达到深度限制后使用评估函数来确定游戏状态的有利性。
算法
这是一个有趣的递归问题，我建议你尝试自己实现一下，不过我的实现可以在下面找到。如果你遇到困难，可以参考以下思路：
-
我们确定一个预定的深度限制k。
-
在第 0 层，我们考虑每一种可能的移动，即子节点。
-
对于每个子节点，我们考虑对手可以迫使我们获得的最低分数。然后，我们选择最高分数的节点。
-
但是要知道对手可以强迫我们获得的最低分数，我们必须转到第 1 层。对于第 1 层中的每个节点，我们考虑它们的子节点。
-
对于每个子节点（对手可能的举动），我们考虑自己后续能够获得的最高分数。然后，对手能够迫使我们获得的最低分数就是最小节点。
-
但要知道我们随后可以获得的最高分数，我们必须进入第 2 层。
-
等等…
-
在第k层，对最终的棋盘状态进行评估并回溯到第 k - 1层，一直持续到第 0 层，此时我们终于可以回答：“此时的最佳走法是什么？”
这是我的实现。请注意，我使用了稍微修改过的chess.js版本，这样我就可以使用game.ugly_moves()和game.ugly_move()来生成和执行走法，而无需将它们转换为人类可读的格式，从而提高了算法的效率。修改后的版本可以在这里找到，但使用普通的game.moves()和game.move()也可以正常工作。
Alpha-beta 剪枝
我们的人工智能现在应该能够做出相当不错的决策。搜索深度越高，它的表现就越好。然而，增加搜索深度会大幅增加执行时间。Alpha -Beta 剪枝算法通过“修剪”不需要评估的分支来帮助提高算法的效率。额外的阅读资源可以在这里找到。
核心理念
alpha-beta 剪枝的核心思想是，当至少发现一种可能性，证明这一举动比之前检查过的举动更糟糕时，我们就可以停止评估这一举动。
假设游戏树如下：
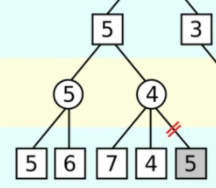
为了简洁起见，我们考虑以下子树：
最大化玩家首先考虑左孩子，并确定它的值为 5。其他路径只有当其值为 时才会被选择x > 5。
接下来考虑右孩子。在右孩子处，最小化玩家目前已经找到了值 7 和 4。但这意味着，无论剩余值是多少，最小化玩家最终得到的最小值最多为 4。我们知道，x <= 4无论剩余值是多少，这棵子树的最终值都是 。
为了使这条路径相关，x > 5。但我们知道x <= 4。这是一个矛盾，所以最大化的玩家不会选择这条路径，进一步评估这条路径也没有意义。
算法
同样的思路可以扩展到游戏树的其余部分。我们使用两个变量alpha和beta来分别跟踪最大值和最小值（上例中分别为 5 和 4）。这只需要对之前的 minimax 函数进行微小修改——看看你是否能自己实现它！
这是我的实现：
结论
就这些！希望你喜欢阅读这篇文章，就像我喜欢写这篇文章一样。我解释了我是如何实现我的人工智能的，并希望向你介绍了一些新的、有趣的概念。
我还实现了一些其他功能，包括让AI自相对抗。你可以在https://zeyu2001.github.io/chess-ai/上体验一下，也可以参考我的GitHub 代码库来了解具体实现。
文章来源：https://dev.to/zeyu2001/build-a-simple-chess-ai-in-javascript-18eg