fp-ts入门:Monad
问题:嵌套上下文
定义
好的但是...为什么?
Kleisli 类别
我们一步步构建构图
法律
单子fp-ts
结论
在上一篇文章中,我们看到我们可以通过提升 来将一个有效程序f: (a: A) => M<B>与一个纯n-ary 程序组合起来,前提是允许一个应用函子实例ggM
| 计划 f | 程序g | 作品 |
|---|---|---|
| 纯的 | 纯的 | g ∘ f |
| 有效的 | 纯的,n-ary |
liftAn(g) ∘ f |
然而我们必须解决最后一种情况:如果两个程序都有效怎么办?
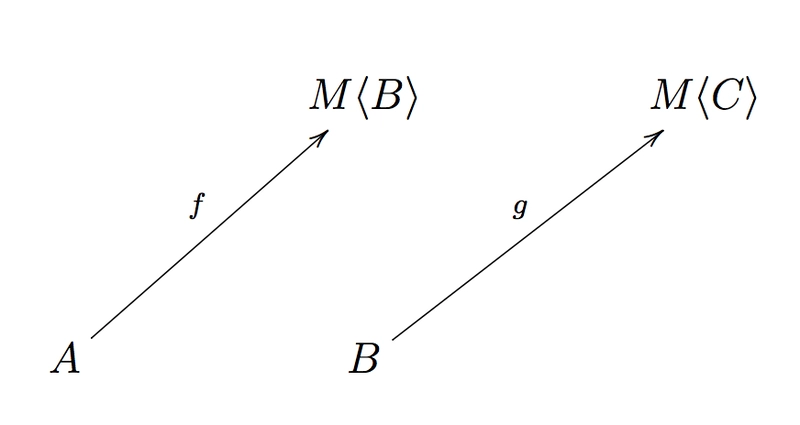
f: (a: A) => M<B>
g: (b: B) => M<C>
f这种和的“组成”是什么g?
为了处理最后一种情况,我们需要比这更强大的东西,Functor因为很容易得到嵌套上下文。
问题:嵌套上下文
为了更好地解释为什么我们需要更多的东西,让我们看一些例子。
例子(M = Array)
假设我们想要检索 Twitter 用户的关注者的关注者:
interface User {
followers: Array<User>
}
const getFollowers = (user: User): Array<User> => user.followers
declare const user: User
const followersOfFollowers: Array<Array<User>> = getFollowers(user).map(getFollowers)
这里有点问题,followersOfFollowers有类型Array<Array<User>>但是我们想要Array<User>。
我们需要展平嵌套数组。
flatten: <A>(mma: Array<Array<A>>) => Array<A>导出的函数很有fp-ts用
import { flatten } from 'fp-ts/Array'
const followersOfFollowers: Array<User> = flatten(getFollowers(user).map(getFollowers))
太棒了!其他数据结构怎么样?
例子(M = Option)
假设我们要计算数字列表头元素的逆
import { Option, some, none, option } from 'fp-ts/Option'
import { head } from 'fp-ts/Array'
const inverse = (n: number): Option<number> => (n === 0 ? none : some(1 / n))
const inverseHead: Option<Option<number>> = option.map(head([1, 2, 3]), inverse)
哎呀,我又做了,inverseHead有类型Option<Option<number>>,但我们想要Option<number>。
我们需要展平嵌套的Options。
import { isNone } from 'fp-ts/Option'
const flatten = <A>(mma: Option<Option<A>>): Option<A> => (isNone(mma) ? none : mma.value)
const inverseHead: Option<number> = flatten(option.map(head([1, 2, 3]), inverse))
所有这些flatten功能...这不是巧合,其背后有一个功能模式。
事实上,所有这些类型构造函数(以及许多其他类型构造函数)都接受一个monad 实例,并且
flatten是单子最特殊的操作
那么什么是 monad?
这就是单子经常呈现的方式……
定义
一个 monad 由以下三件事定义:
M(1)接受Functor实例的类型构造函数
of(2)具有以下签名的函数
of: <A>(a: A) => HKT<M, A>
flatMap(3)具有以下签名的函数
flatMap: <A, B>(f: (a: A) => HKT<M, B>) => ((ma: HKT<M, A>) => HKT<M, B>)
注意:回想一下,HKT类型是fp-ts表示泛型类型构造函数的方式,因此当您看到时,HKT<M, X>您可以想到将类型构造函数M应用于类型X(即M<X>)。
这些职能of必须flatMap遵循三条规律:
flatMap(of) ∘ f = f(左恒等式)flatMap(f) ∘ of = f(正确身份)flatMap(h) ∘ (flatMap(g) ∘ f) = flatMap((flatMap(h) ∘ g)) ∘ f(结合性)
其中f,,均为有效函数,g为通常的函数组合。h∘
好的但是...为什么?
当我第一次看到这样的定义时,我的第一反应是困惑。
所有这些问题都在我的脑海里盘旋:
- 为什么是这两个特定的操作以及它们为什么具有这些类型?
- 为什么叫“flatMap”?
- 为什么要制定这些法律?它们意味着什么?
- 但最重要的是,我的在哪里
flatten?
这篇文章将尝试回答每一个问题。
让我们回到我们的问题:两个有效函数(也称为Kleisli 箭头)的组合是什么?
我甚至不知道它的类型是什么。
等等……我们已经接触过一个关于组合的抽象概念了。你还记得我之前说过的范畴吗?
类别抓住了构图的本质
我们可以将我们的问题转化为一个分类问题:我们能否找到一个可以模拟克莱斯利箭头组成的类别?
Kleisli 类别
让我们尝试构建一个仅包含有效函数的类别K(名为Kleisli 类别):
- 这些对象是TS类别的相同对象,即所有 TypeScript 类型。
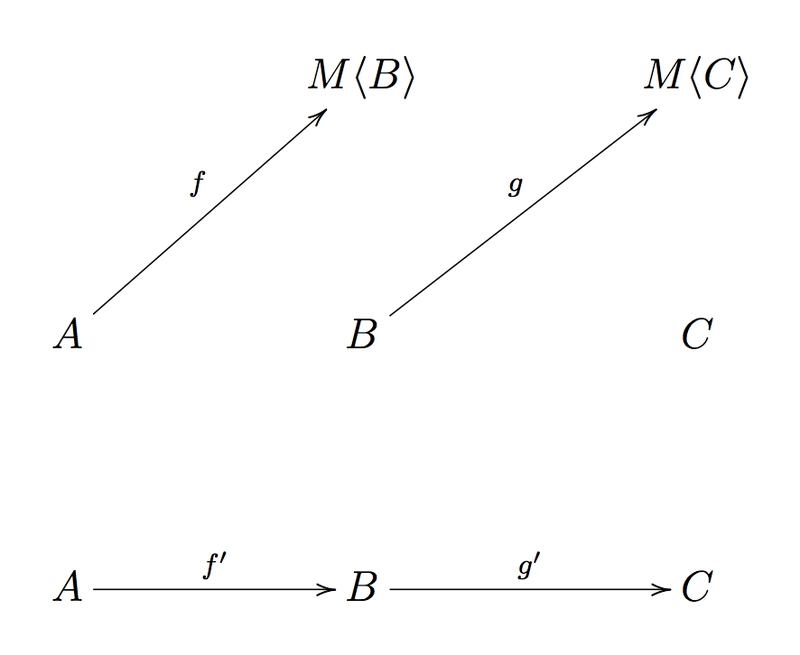
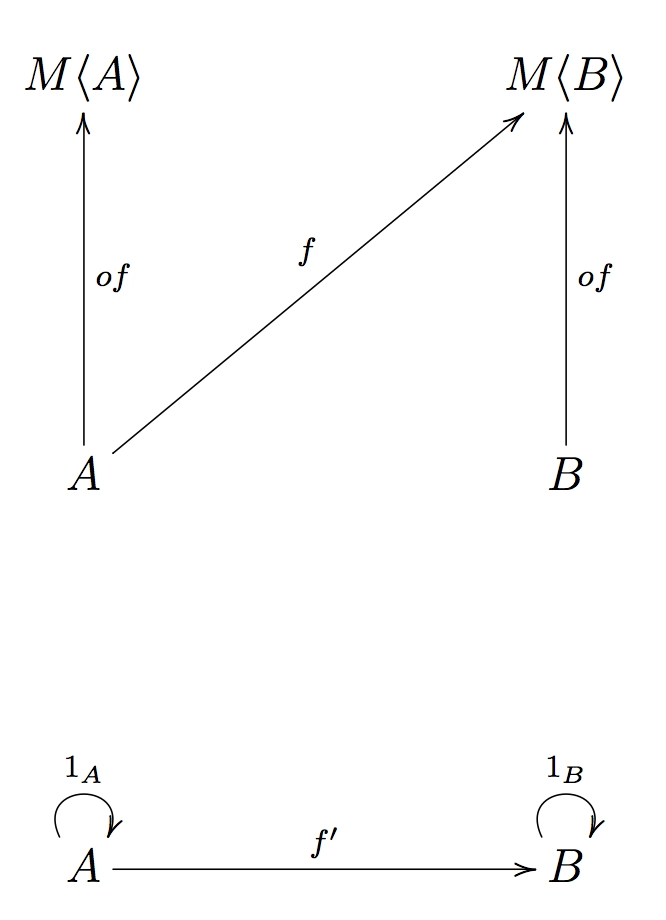
- 态射是这样构建的:每当TS
f: A ⟼ M<B>中有一个 Kleisli 箭头时,我们就在K中画一个箭头f': A ⟼ B
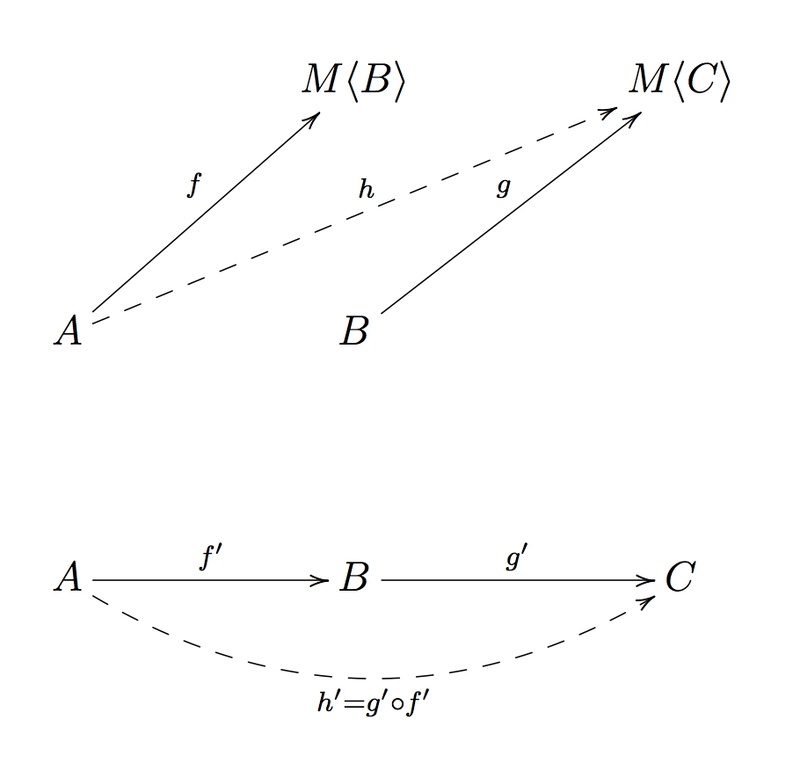
那么K中的f'和的组成是什么?这就是下图中虚线箭头所指的。g'h'
由于h'是从A到 的箭头,因此在 中C应该有一个h从A到 的对应函数。M<C>TS
因此, TS中f和的组合的良好候选仍然是具有以下签名的有效函数:。g(a: A) => M<C>
我们如何构建这样的函数?好吧,我们来试试吧!
我们一步步构建构图
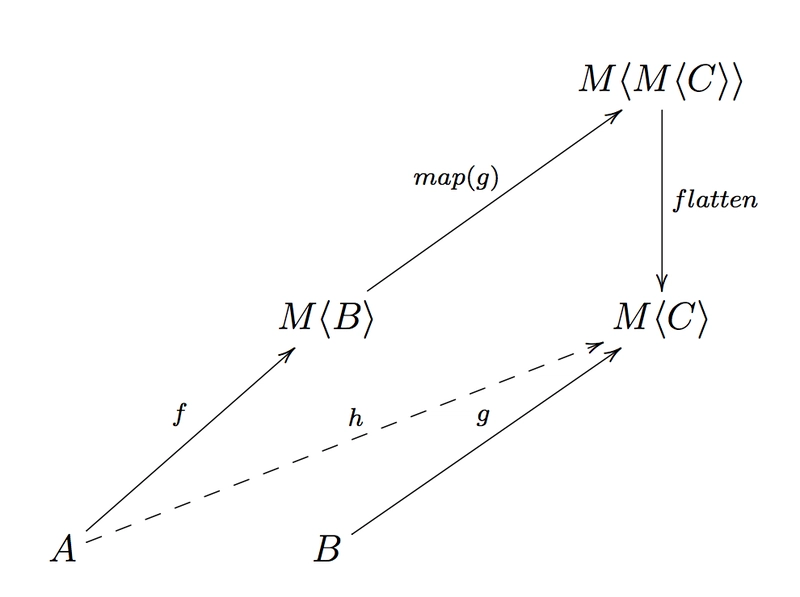
monad 定义的 (1) 点表示M允许一个函子实例,因此我们可以将lift函数g: (b: B) => M<C>转换为函数lift(g): (mb: M<B>) => M<M<C>>(这里我使用它的同义词map)
现在我们陷入了困境:函子实例上没有合法的操作能够将类型的值展平M<M<C>>为类型的值M<C>,我们需要一个额外的flatten操作。
如果我们可以定义这样的操作,那么我们就可以得到我们正在寻找的组合
h = flatten ∘ map(g) ∘ f
但是等一下,flatten ∘ map(g)是flatMap,这就是这个名字的由来!
h = flatMap(g) ∘ f
我们现在可以更新我们的“组成表”
| 计划 f | 程序g | 作品 |
|---|---|---|
| 纯的 | 纯的 | g ∘ f |
| 有效的 | 纯的,n-ary |
liftAn(g) ∘ f |
| 有效的 | 有效的 | flatMap(g) ∘ f |
那么 呢of? 嗯,of它来自于K中的恒等态射:对于K中的每个恒等态射 1 A ,都应该有一个从到 的函数对应(即)。AM<A>of: <A>(a: A) => M<A>
法律
最后一个问题:这些定律从何而来?它们只是K中的范畴定律被翻译成TS的形式:
| 法律 | 钾 | TS |
|---|---|---|
| 左翼身份 | 1 B ∘ f'=f' |
flatMap(of) ∘ f = f |
| 正确的身份 | f'∘ 1 A =f' |
flatMap(f) ∘ of = f |
| 结合性 | h' ∘ (g' ∘ f') = (h' ∘ g') ∘ f' |
flatMap(h) ∘ (flatMap(g) ∘ f) = flatMap((flatMap(h) ∘ g)) ∘ f |
单子fp-ts
在fp-ts函数中flatMap,通过一个名为的变体进行建模chain,该变体基本上是flatMap重新排列参数的
flatMap: <A, B>(f: (a: A) => HKT<M, B>) => ((ma: HKT<M, A>) => HKT<M, B>)
chain: <A, B>(ma: HKT<M, A>, f: (a: A) => HKT<M, B>) => HKT<M, B>
请注意,chain可以从中得出flatMap(反之亦然)。
现在,如果我们回到展示嵌套上下文问题的示例,我们可以通过使用chain
import { array, head } from 'fp-ts/Array'
import { Option, option } from 'fp-ts/Option'
const followersOfFollowers: Array<User> = array.chain(getFollowers(user), getFollowers)
const headInverse: Option<number> = option.chain(head([1, 2, 3]), inverse)
结论
函数式编程提供了组合具有效果的函数的通用方法:函子、应用函子和 monad 都是抽象概念,它们为组合不同类型的程序提供了原则性的工具。
TLDR:函数式编程实际上就是组合
鏂囩珷鏉ユ簮锛�https://dev.to/gcanti/getting-started-with-fp-ts-monad-6k 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com