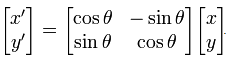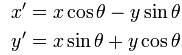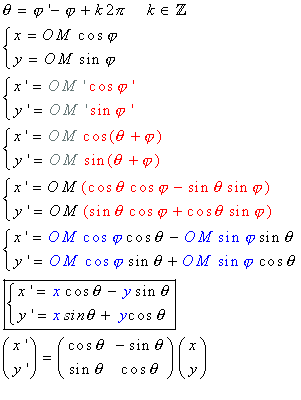TypeScript 中的函数式编程
内容
源代码:https://github.com/aelassas/ functional-ts
介绍
在 TypeScript 中,函数就是对象。因此,函数可以被构造、作为参数传递、从函数返回或赋值给变量。因此,TypeScript 拥有“一等函数”。更准确地说,TypeScript 支持以下功能:
- 高阶函数参数
- 高阶函数结果
- 嵌套函数
- 匿名函数
- 闭包
- 部分应用(ECMAScript 5)
本文不会讨论函数式编程的基础知识,因为您可以找到大量相关资源。相反,本文将讨论 TypeScript 中函数式编程在代数、数字、欧氏平面和分形中的应用。本文提供的示例将由简入繁,但始终以简单、直接且易于理解的方式进行说明。
TypeScript 环境
要运行源代码,您需要安装Node.js。安装 Node.js 后,克隆 GitHub 存储库:
git clone https://github.com/aelassas/functional-ts.git
转到源代码文件夹,设置 TypeScript 环境并使用以下命令安装所有必要的依赖项:
cd functional-ts
npm install
要运行数字演示,请运行以下命令:
npm run numbers
要运行欧几里得平面演示,请运行以下命令:
npm run plane
要运行分形演示,请运行以下命令:
npm run fractals
要运行单元测试,请运行以下命令:
npm test
通过函数表示数据
令为任意元素, , ...S的集合(例如,桌子上的书或欧氏平面的点),令为这些元素的任意子集(例如,桌子上的绿色书或以欧氏平面原点为中心、半径为 1 的圆内的点)。abcS'
集合的特征函数 是将或与的每个元素相关联的函数。S'(x)S'truefalsexS
S'(x) = true if x is in S'
S'(x) = false if x is not in S'
设S为桌子上的书籍集合,设S'为桌子上的绿色书籍集合。设a和b为两本绿色书籍,设c和d为桌子上的两本红色书籍。则:
S'(a) = S'(b) = true
S'(c) = S'(d) = false
设S为欧氏平面中的点集,设S'为以欧氏平面原点 (0, 0) 为圆心,半径为 1 的圆(单位圆)中的点集。设a和b为单位圆中的两个点,设c和d为以欧氏平面原点为圆心,半径为 2 的圆中的两个点。则:
S'(a) = S'(b) = true
S'(c) = S'(d) = false
因此,任何集合都可以用其特征函数S'来表示。该函数以元素为参数,如果该元素在 中则返回结果,否则返回结果。换句话说,集合(抽象数据类型)在 TypeScript 中可以用函数来表示。trueS'false
type Set<T> = (x: T) => boolean
在接下来的部分中,我们将学习如何通过 TypeScript 以函数式的方式表示集合代数中的一些基本集合,然后定义集合上的通用二元运算。之后,我们将把这些运算应用于数字,然后应用于欧氏平面的子集。集合是抽象的数据结构,数字的子集和欧氏平面的子集是抽象数据结构的表示,最后,二元运算是适用于任何抽象数据结构表示的通用逻辑。
套
本节通过 TypeScript 介绍集合代数中一些基本集合的表示。
空集
设E为空集,Empty其特征函数 为。在集合代数中,E是唯一不含元素的集合。因此,Empty可以定义如下:
Empty(x) = false if x is in E
Empty(x) = false if x is not in E
因此,在 TypeScript 中的表示E可以定义如下:
const empty = <T>() => (e: T) => false
在集合代数中,Empty表示如下:
因此,运行下面的代码:
console.log('\nEmpty set:')
console.log('Is 7 in {}?', common.empty<number>()(7))
给出以下结果:
设置全部
设S为集合,为包含所有元素的S'子集,其特征函数为。在集合代数中,是包含所有元素的全集。因此,可以定义如下:SAllS'All
All(x) = true if x is in S
因此,在 TypeScript 中的表示S'可以定义如下:
const all = <T>() => (e: T) => true
在集合代数中,All表示如下:
因此,运行下面的代码:
console.log('\nSet All:')
console.log('Is 7 in integers set?', common.all<number>()(7))
给出以下结果:
单例集
设E为单例集,Singleton其特征函数 为。在集合代数中,E也称为单位集或一元组,是指只有一个元素 的集合e。因此,Singleton可以定义如下:
Singleton(x) = true if x is e
Singleton(x) = false if x is not e
因此,在 TypeScript 中的表示E可以定义如下:
const singleton = <T>(x: T) => (y: T) => x === y
因此,运行下面的代码:
console.log('\nSingleton set:')
console.log('Is 7 in the singleton set {0}?', common.singleton(0)(7))
console.log('Is 7 in the singleton set {7}?', common.singleton(7)(7)
给出以下结果:
其他套装
本节介绍整数集的子集。
偶数
设E为偶数集,Even其特征函数 为。在数学中,偶数是指2的倍数。因此,Even可以定义如下:
Even(x) = true if x is a multiple of 2
Even(x) = false if x is not a multiple of 2
因此,在 TypeScript 中的表示E可以定义如下:
const even = (x: number) => x % 2 === 0
因此,运行下面的代码:
console.log('\nEven numbers set:')
console.log('Is 99 in even numbers set?', numbers.even(99))
console.log('Is 998 in even numbers set?', numbers.even(998))
给出以下结果:
奇数
设E为奇数集,Odd其特征函数 为。在数学中,奇数是指不是2的倍数的数。因此,Odd可以定义如下:
Odd(x) = true if x is not a multiple of 2
Odd(x) = false if x is a multiple of 2
因此,在 TypeScript 中的表示E可以定义如下:
const odd = (x: number) => x % 2 === 1
因此,运行下面的代码:
console.log('\nOdd numbers set:')
console.log('Is 99 in odd numbers set?', numbers.odd(99))
console.log('Is 998 in odd numbers set?', numbers.odd(998))
给出以下结果:
3 的倍数
设E为3的倍数集,MultipleOfThree其特征函数为。在数学中,3的倍数是指能被3整除的数。因此,MultipleOfThree可以定义如下:
MultipleOfThree(x) = true if x is divisible by 3
MultipleOfThree(x) = false if x is not divisible by 3
因此,在 TypeScript 中的表示E可以定义如下:
jsconst multipleOfThree = (x: number) => x % 3 === 0
因此,运行下面的代码:
console.log('\nMultiples of 3 set:')
console.log('Is 99 in multiples of 3 set?', numbers.multipleOfThree(99))
console.log('Is 998 in multiples of 3 set?', numbers.multipleOfThree(998))
给出以下结果:
5 的倍数
设E为5的倍数集,MultipleOfFive其特征函数为。在数学中,5的倍数是指能被5整除的数。因此,MultipleOfFive可以定义如下:
MultipleOfFive(x) = true if x is divisible by 5
MultipleOfFive(x) = false if x is not divisible by 5
因此,在 TypeScript 中的表示E可以定义如下:
jsconst multipleOfFive = (x: number) => x % 5 === 0
因此,运行下面的代码:
console.log('\nMultiples of 5 set:')
console.log('Is 15 in multiples of 5 set?', numbers.multipleOfFive(15))
console.log('Is 998 in multiples of 5 set?', numbers.multipleOfFive(998))
给出以下结果:
质数
很久以前,当我在研究欧拉计划问题时,我必须解决以下问题:
By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13,
we can see that the 6th prime is 13.
What is the 10 001st prime number?
为了解决这个问题,我首先需要编写一个快速算法来检查给定数字是否为素数。算法写好后,我又编写了一个迭代算法,迭代所有素数,直到找到第 10001 个素数。
设E为素数集,Prime其特征函数 为。在数学中,素数是指大于1的自然数,除1和其本身外没有其他正因数。因此,Prime可以定义如下:
Prime(x) = true if x is prime
Prime(x) = false if x is not prime
因此,在 TypeScript 中的表示E可以定义如下:
const prime = (x: number) => {
if (x <= 1) return false
if (x < 4) return true
if (x % 2 === 0) return false
if (x < 9) return true
if (x % 3 === 0) return false
const sqrt = Math.sqrt(x)
for (let i = 5; i <= sqrt; i += 6) {
if (x % i === 0) return false
if (x % (i + 2) === 0) return false
}
return true
}
因此,运行下面的代码来解决我们的问题:
console.log('\nPrimes set:')
console.log('Is 2 in primes set?', numbers.prime(2))
console.log('Is 4 in primes set?', numbers.prime(4))
console.log('The 10 001st prime number is', numbers.getPrime(10001))
其中getPrime定义如下:
const getPrime = (p: number) => {
for (let i = 1, count = 0; ; i++) {
if (prime(i)) count++
if (count === p) return i
}
}
给出以下结果:
二元运算
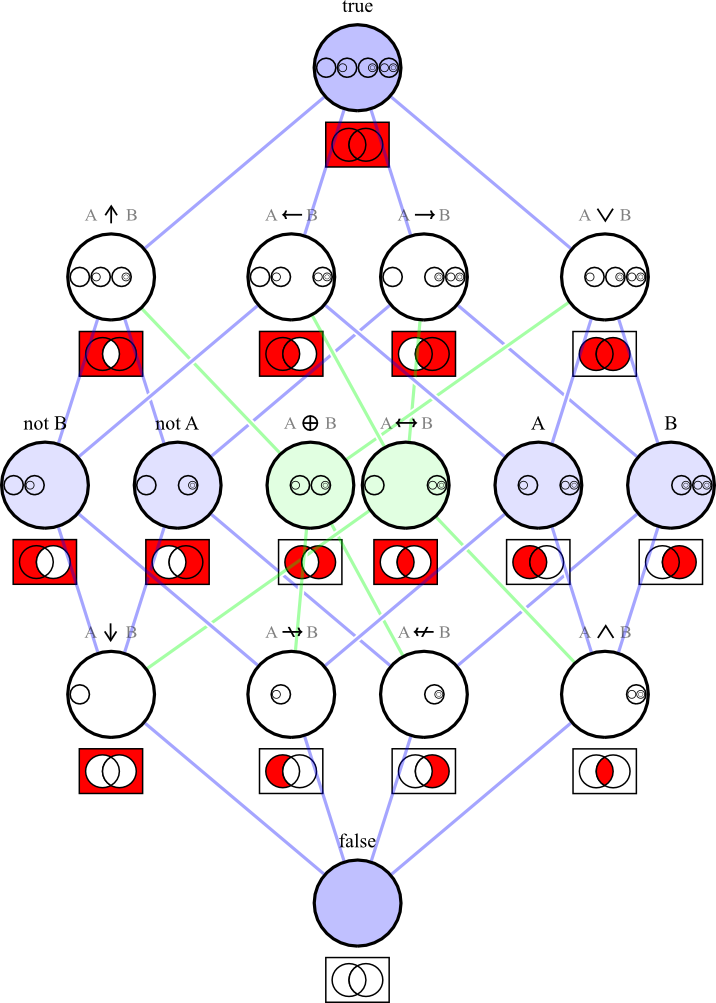
本节介绍从给定集合构造新集合以及操作集合的几种基本运算。下图是集合代数中的维恩图。
联盟
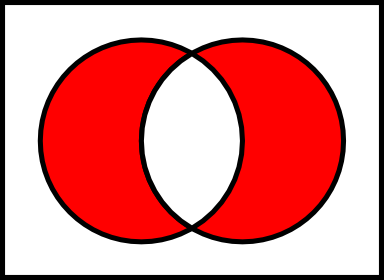
设E和F为两个集合。和的并集,记为,是所有属于和的元素的集合。EFE U FEF
设Union为并集运算。因此,该Union运算可以在 TypeScript 中按如下方式实现:
const union = <T>(e: Set<T>, f: Set<T>) => (x: T) => e(x) || f(x)
运行下面的代码:
console.log('\nUnion:')
console.log('Is 7 in the union of Even and Odd Integers Set?', core.union(numbers.even, numbers.odd)(7))
给出以下结果:
路口
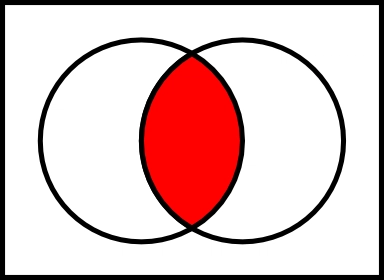
设E和F为两个集合。和的交集,记为,是所有同时属于和的元素的集合。EFE n FEF
令Intersection为交集运算。因此,该Intersection运算可以在 TypeScript 中实现如下:
jsconst intersection = <T>(e: Set<T>, f: Set<T>) => (x: T) => e(x) && f(x)
运行下面的代码:
console.log('\nIntersection:')
const multiplesOfThreeAndFive = core.intersection(numbers.multipleOfThree, numbers.multipleOfFive)
console.log('Is 15 a multiple of 3 and 5?', multiplesOfThreeAndFive(15))
console.log('Is 10 a multiple of 3 and 5?', multiplesOfThreeAndFive(10))
给出以下结果:
笛卡尔积
设E和F为两个集合。和的笛卡尔积,记为,是所有有序对的集合,其中,是的成员,是的成员。EFE × F(e, f)eEfF
令CartesianProduct为笛卡尔积运算。因此,该CartesianProduct运算可以在 TypeScript 中实现如下:
const cartesianProduct = <T1, T2>(e: Set<T1>, f: Set<T2>) => (x: T1, y: T2) => e(x) && f(y)
运行下面的代码:
console.log('\nCartesian Product:')
const cp = core.cartesianProduct(numbers.multipleOfThree, numbers.multipleOfFive)
console.log('Is (9, 15) in MultipleOfThree x MultipleOfFive? ', cp(9, 15))
给出以下结果:
补充
设E和F为两个集合。在中的相对补集,记为,是所有属于但不是属于的元素的集合。FEE \ FEF
令Complement为相对补运算。因此,该Complement运算可以在 TypeScript 中实现如下:
const complement = <T>(e: Set<T>, f: Set<T>) => (x: T) => e(x) && !f(x)```
Running the code below:
```js
console.log('\nComplement:')
const c = core.complement(numbers.multipleOfThree, numbers.multipleOfFive)
console.log('Is 15 in MultipleOfThree \\ MultipleOfFive set? ', c(15))
console.log('Is 9 in MultipleOfThree \\ MultipleOfFive set? ', c(9))
给出以下结果:
对称差分
设E和F为两个集合。和的对称差,记为,是所有属于和但不属于和的交集的元素的集合。EFE Δ FEFEF
设SymmetricDifference为对称差分运算。因此,该SymmetricDifference运算在 TypeScript 中可以通过两种方式实现。一种简单的方法是使用并集和补集运算,如下所示:
const symmetricDifferenceWithoutXor = <T>(e: Set<T>, f: Set<T>) =>
(x: T) => union(complement<T>(e, f), complement(f, e))(x)
另一种方法是使用XOR二元运算,如下所示:
const symmetricDifferenceWithXor = <T>(e: Set<T>, f: Set<T>) => (x: T) => e(x) !== f(x)
运行下面的代码:
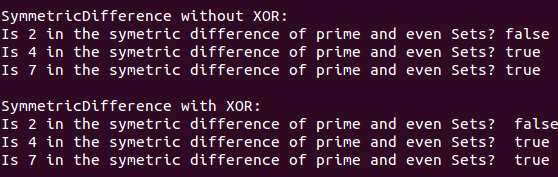
console.log('\nSymmetricDifference without XOR:')
const sdWithoutXor = core.symmetricDifferenceWithoutXor(numbers.prime, numbers.even)
console.log('Is 2 in the symetric difference of prime and even Sets? ', sdWithoutXor(2))
console.log('Is 4 in the symetric difference of prime and even Sets? ', sdWithoutXor(4))
console.log('Is 7 in the symetric difference of prime and even Sets? ', sdWithoutXor(7))
console.log('\nSymmetricDifference with XOR:')
const sdWithXor = core.symmetricDifferenceWithXor(numbers.prime, numbers.even)
console.log('Is 2 in the symetric difference of prime and even Sets? ', sdWithXor(2))
console.log('Is 4 in the symetric difference of prime and even Sets? ', sdWithXor(4))
console.log('Is 7 in the symetric difference of prime and even Sets? ', sdWithXor(7))
给出以下结果:
其他操作
本节介绍集合上的其他有用的二元运算。
包含
设为Contains检查元素是否在集合中的操作。此操作是一个函数,它以元素为参数,true如果元素在集合中则返回结果,false否则返回结果。
因此,此操作在 TypeScript 中定义如下:
const contains = <T>(e: Set<T>, x: T) => e(x)
因此,运行下面的代码:
console.log('\nContains:')
console.log('Is 7 in the singleton {0}? ', core.contains(common.singleton(0), 7))
console.log('Is 7 in the singleton {7}? ', core.contains(common.singleton(7), 7))
给出以下结果:
添加
设Add为将元素添加到集合的操作。此操作是一个函数,它以元素为参数,并将其添加到集合中。
因此,此操作在 TypeScript 中定义如下:
const add = <T>(e: Set<T>, y: T) => (x: T) => x === y || e(x)
因此,运行下面的代码:
console.log('\nAdd:')
console.log('Is 7 in {0, 7}? ', core.add<number>(common.singleton(0), 7)(7))
console.log('Is 0 in {1, 0}? ', core.add<number>(common.singleton(1), 0)(0))
console.log('Is 7 in {19, 0}? ', core.add<number>(common.singleton(19), 0)(7))
给出以下结果:
消除
表示Remove从集合中删除元素的操作。该操作是一个函数,它接受一个元素作为参数,并将其从集合中删除。
因此,此操作在 TypeScript 中定义如下:
const remove = <T>(e: Set<T>, y: T) => (x: T) => x !== y && e(x)
因此,运行下面的代码:
console.log('\nRemove:')
console.log('Is 7 in {}? ', core.remove<number>(common.singleton(0), 0)(7))
console.log('Is 0 in {}? ', core.remove<number>(common.singleton(7), 7)(0))
给出以下结果:
对于那些想要更进一步的人
您可以看到,通过函数式编程,我们可以在 TypeScript 中轻松地进行一些集合代数运算。前面几节展示了最基本的定义。但是,如果您想更进一步,可以思考:
- 集合上的关系
- 抽象代数,例如幺半群、群、域、环、K-向量空间等
- 容斥原理
- 罗素悖论
- 康托尔悖论
- 对偶向量空间
- 定理和推论
欧几里得平面
上一节中,我们用 TypeScript 实现了集合的基本概念。本节我们将练习在欧氏平面上实现的概念。
绘制磁盘
圆盘是平面的一个子集,其边界由圆组成。圆盘有两种类型:闭盘,其边界包含构成其边界的圆的点;开盘,其边界不包含构成其边界的圆的点。
在本节中,我们将设置封闭磁盘的Characterstic 功能并将其绘制在 HTML5 页面中。
要设置Characterstic 函数,我们首先需要一个函数来计算平面上两点之间的欧氏距离。该函数实现如下:
function distance(p1: Point, p2: Point) {
return Math.sqrt((p1.x - p2.x) ** 2 + (p1.y - p2.y) ** 2)
}
其中Point定义如下:
class Point {
x: number
y: number
constructor(x: number, y: number) {
this.x = x
this.y = y
}
}
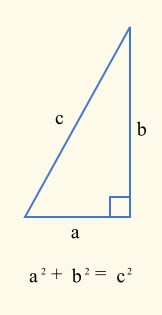
该公式基于勾股定理。
其中c是欧氏距离,a²是(p1.X - p2.X)²,b²是(p1.Y - p2.Y)²。
设Disk为闭圆盘的特征函数。在集合代数中,实数集中闭圆盘的定义如下:
其中a和b分别是中心和R半径的坐标。
因此,在 TypeScript 中的实现Disk如下:
const disk = (center: Point, radius: number) => (p: Point) => distance(p, center) <= radius
为了在 HTML5 页面中查看集合,我决定实现一个在欧氏平面draw中绘制集合的函数。我选择了HTML5,因此使用元素进行绘制。canvas
于是,我通过 的方法构建了下面所示的欧几里得平面draw。
下面是平面的实现。
class Plane {
width: number
height: number
constructor(width: number, height: number) {
this.width = width
this.height = height
}
draw(set: PlaneSet, canvasId: string) {
const canvas = document.getElementById(canvasId) as HTMLCanvasElement
if (!canvas) throw new Error(`Canvas with id ${canvasId} not found`)
canvas.width = this.width
canvas.height = this.height
const context = canvas.getContext('2d') as CanvasRenderingContext2D
const semiWidth = this.width / 2
const semiHeight = this.height / 2
const xMin = -semiWidth
const xMax = semiWidth
const yMin = -semiHeight
const yMax = semiHeight
for (let x = 0; x < this.width; x++) {
const xp = xMin + (x * (xMax - xMin)) / this.width
for (let y = 0; y < this.height; y++) {
const yp = yMax - (y * (yMax - yMin)) / this.height
if (set(new Point(xp, yp))) context.fillRect(x, y, 1, 1)
}
}
}
clear(canvasId: string) {
const canvas = document.getElementById(canvasId) as HTMLCanvasElement
if (!canvas) throw new Error(`Canvas with id ${canvasId} not found`)
const context = canvas.getContext('2d') as CanvasRenderingContext2D
context.clearRect(0, 0, this.width, this.height)
}
}
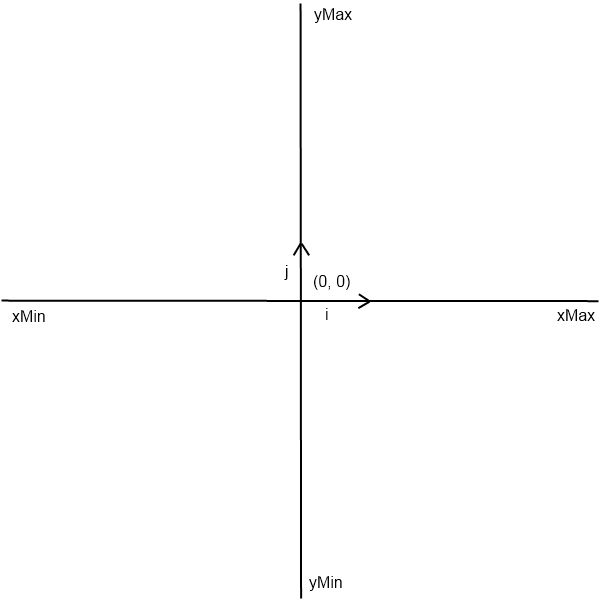
在该draw函数中,创建一个与欧氏平面canvas容器具有相同宽度和高度的。然后,如果中的每个点(以像素为单位)属于 ,则将其替换为黑点。、和是上图欧氏平面图中所示的边界值。(x,y)canvassetxMinxMaxyMinyMax
运行下面的代码:
euclideanPlane = new Plane(200, 200)
euclideanPlane.draw(disk(new Point(0, 0), 50), 'disk')
画布的disk在哪里:id
<canvas id="disk"></canvas>
给出以下结果:
绘制水平和垂直半平面
水平半平面或垂直半平面是平面将欧氏空间划分成的两个子集之一。水平半平面是平面通过垂直于Y 轴的直线将欧氏空间划分成的两个子集之一,如上图所示。垂直半平面是平面通过垂直于X 轴的直线将欧氏空间划分成的两个子集之一。
在本节中,我们将设置水平和垂直半平面的特征函数,在 HTML5 页面中绘制它们,并查看如果将它们与磁盘子集结合起来可以做什么。
令HorizontalHalfPlane为水平半平面的特征函数。在 TypeScript 中的实现如下:HorizontalHalfPlane
const horizontalHalfPlane = (y: number, isLowerThan: boolean) =>
(p: Point) => (isLowerThan ? p.y <= y : p.y >= y)
因此,运行下面的代码:
euclideanPlane.draw(horizontalHalfPlane(0, true),'hhp')
画布的hhp在哪里:id
<canvas id="hhp"></canvas>
给出以下结果:
令VerticalHalfPlane为垂直半平面的特征函数。在 TypeScript 中的实现如下:VerticalHalfPlane
jsconst verticalHalfPlane = (x: number, isLowerThan: boolean) =>
(p: Point) => (isLowerThan ? p.x <= x : p.x >= x)
因此,运行下面的代码:
euclideanPlane.draw(verticalHalfPlane(0, false),'vhp')
画布的vhd在哪里:id
<canvas id="vhd"></canvas>
给出以下结果:
disk在文章的第一部分,我们建立了集合的基本二元运算。因此,例如,通过组合a和a的交集half-plane,我们可以绘制半圆盘子集。
因此,运行下面的示例:
euclideanPlane.draw(set.intersection(disk(new Point(0, 0), 50),
verticalHalfPlane(0, false)), 'hd')
画布的hd在哪里:id
<canvas id="hd"></canvas>
给出以下结果:
功能
本节介绍欧几里得平面集合上的函数。
翻译
设translatePoint为平移平面上某个点的函数。在欧几里得几何中,translatePoint是一个将给定点沿指定方向移动恒定距离的函数。因此,在 TypeScript 中的实现如下:
const translatePoint = (deltax: number, deltay: number) =>
(p: Point) => new Point(p.x + deltax, p.y + deltay)
其中(deltax, deltay)是平移的常向量。
设translate为在平面上平移集合的函数。该函数在 TypeScript 中的实现如下:
const translate = (e: PlaneSet, deltax: number, deltay: number) =>
(p: Point) => e(translatePoint(-deltax, -deltay)(p))
translate以 为参数,deltax分别为第一个欧氏维度上的增量距离和deltay第二个欧氏维度上的增量距离。如果点P (x, y)在集合S中平移,则其坐标将变为(x', y') = (x, delatx, y, deltay)。因此,点(x' - delatx, y' - deltay)将始终属于集合S。在集合代数中,translate被称为同构,换句话说,所有平移的集合构成平移群 T,它与空间本身同构。这解释了该函数的主要逻辑。
因此,在我们的 HTML5 页面中运行下面的代码:
let translate_timer: ReturnType<typeof setInterval>
function translate_op() {
let deltay = 0
clearTimeout(scale_timer)
clearTimeout(rotate_timer)
translate_timer = setInterval(() => {
deltay = deltay <= euclideanPlane.height ? deltay + 20 : 0
euclideanPlane.draw(translate(disk(new Point(0, -50), 50), 0, deltay), 'ep_op')
}, 1000)
}
画布的ep_op在哪里:id
<canvas id="ep_op"></canvas>
给出以下结果:
同质性
设为将任意点M连接到另一点N 的scalePoint函数,使得线段SN与SM位于同一直线上,但缩放了因子 λ。在集合代数中,公式如下:Scale
因此在 TypeScript 中的实现如下:
const scalePoint = (lambdax: number, lambday: number, deltax: number, deltay: number)
=> (p: Point) => new Point(lambdax * p.x + deltax, lambday * p.y + deltay)
其中(deltax, deltay)是平移的常向量,(lambdax, lambday)是 lambda 向量。
设scale该函数用于对计划中的集合应用同位性。该函数在 TypeScript 中的实现如下:
const scale = (e: PlaneSet, lambdax: number, lambday: number, deltax: number,
deltay: number) => (p: Point) => e(scalePoint(1 / lambdax, 1 / lambday,
-deltax / lambdax, -deltay / lambday)(p))
scale以作为参数,deltax是第一个欧几里得维度中的增量距离,deltay是第二个欧几里得维度中的增量距离,(lambdax, lambday)是常数因子向量λ。如果点P (x, y)scale在集合S中变换,则其坐标将变为(x', y') = (lambdax * x, delatx, lambday * y, deltay)。因此,点((x'- delatx)/lambdax, (y' - deltay)/lambday)将始终属于集合S,当然,如果 lambda 与向量 0 不同。在集合代数中,scale被称为同构,换句话说,所有同构体的集合形成同构群 H,它同构于空间本身 \ {0}。这解释了函数的主要逻辑。
因此,在我们的 HTML5 页面中运行下面的代码:
let scale_timer: ReturnType<typeof setInterval>
function scale_op() {
let deltay = 0
let lambday = 0.05
clearTimeout(translate_timer)
clearTimeout(rotate_timer)
scale_timer = setInterval(() => {
deltay = deltay <= euclideanPlane.height ? deltay + 20 : 0
lambday = deltay <= euclideanPlane.height ? lambday + 0.05 : 0.05
euclideanPlane.draw(scale(disk(new Point(0, -50), 50), 1, lambday, 0, deltay), 'ep_op')
}, 1000)
}
给出以下结果:
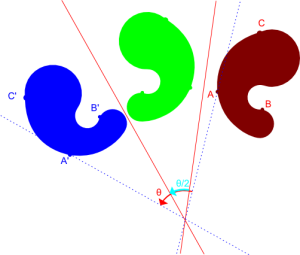
旋转
令rotatePoint为将点旋转角度为 θ 的函数。在矩阵代数中,rotatePoint公式如下:
其中(x',y')是旋转后点的坐标,x'和y'的公式如下:
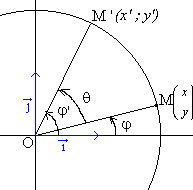
这个公式的演示非常简单。看看这个旋转。
下面演示:
因此在 TypeScript 中的实现如下:
const rotatePoint = (theta: number) => (p: Point) => new Point(p.x * Math.cos(theta)
- p.y * Math.sin(theta), p.x * Math.sin(theta) + p.y * Math.cos(theta))
设rotate为对平面上的集合进行角度为 θ 的旋转的函数。该函数在 TypeScript 中的实现如下。
const rotate = (e: PlaneSet, theta: number) => (p: Point) => e(rotatePoint(-theta)(p))
rotatetheta是一个以旋转角度为参数的函数。如果点P (x, y)rotate在集合S中经过变换,则其坐标将变为(x', y') = (x * cos(theta) - y * sin(theta), x * sin(theta), y * cos(theta))。因此,点(x' * cos(theta), y' * sin(theta), y' * cos(theta) - x' * sin(theta))将始终属于集合S。在集合代数中,rotate这被称为同构,换句话说,所有旋转的集合构成旋转群 R,它与空间本身同构。这解释了该函数的主要逻辑。
因此,在我们的 HTML5 页面中运行下面的代码:
let rotate_timer: ReturnType<typeof setInterval>
function rotate_op() {
let theta = 0
clearTimeout(translate_timer)
clearTimeout(scale_timer)
rotate_timer = setInterval(() => {
euclideanPlane.draw(rotate(horizontalHalfPlane(-90, true), theta), 'ep_op')
theta = (theta + Math.PI / 2) % (2 * Math.PI)
}, 1000)
}
给出以下结果:
对于那些想要更进一步的人
很简单,不是吗?想要更进一步了解的朋友,可以探索一下:
- 椭圆
- 三维欧几里得空间
- 椭圆体
- 抛物面
- 双曲面
- 球谐函数
- 超椭圆体
- 妊神星
- 同种异体
- 焦平面
分形

分形是指分形维数通常超过其拓扑维数且可能介于整数之间的集合。例如,曼德布洛特集就是由一族复二次多项式定义的分形:
Pc(z) = z^2 + c
其中c是一个复数。曼德布洛特分形定义为所有满足c上述序列不会趋于无穷大的点的集合。在集合代数中,其公式如下:
分形(抽象数据类型)在 TypeScript 中始终可以表示如下:
type Fractal = (z: Complex, c: Complex) => Complex
复数与绘画
为了能够绘制分形,我需要操作复数。因此,我创建了Complex以下类:
class Complex {
x: number
y: number
static zero = new Complex(0, 0)
constructor(x: number, y: number) {
this.x = x
this.y = y
}
abs() {
return Math.sqrt(this.x * this.x + this.y * this.y)
}
toString() {
return this.x + ' + i * ' + this.y
}
}
function add(z1: Complex, z2: Complex) {
return new Complex(z1.x + z2.x, z1.y + z2.y)
}
function substract(z1: Complex, z2: Complex) {
return new Complex(z1.x - z2.x, z1.y - z2.y)
}
function multiply(z1: Complex, z2: Complex) {
return new Complex(z1.x * z2.x - z1.y * z2.y, z1.x * z2.y + z1.y * z2.x)
}
曼德布洛特分形
我创建了一个曼德布洛特分形(抽象数据类型表示),P(z) = z^2 + c如下所示。
const mandelbrot = (z: Complex, c: Complex) => add(multiply(z, z), c)
为了能够绘制复数,我创建了一个ComplexPlane类。下面是 TypeScript 中的实现。
class ComplexPlane {
width: number
height: number
real_min: number
real_max: number
imaginary_min: number
imaginary_max: number
boundary: number
fractalIterationsPerPixel: number
canvasId: string
constructor(
width: number,
height: number,
real_min: number,
real_max: number,
imaginary_min: number,
imaginary_max: number,
boundary: number,
fractalIterationsPerPixel: number,
canvasId: string,
) {
this.width = width
this.height = height
this.real_min = real_min
this.real_max = real_max
this.imaginary_min = imaginary_min
this.imaginary_max = imaginary_max
this.boundary = boundary
this.fractalIterationsPerPixel = fractalIterationsPerPixel
this.canvasId = canvasId
}
draw(fractal: Fractal) {
const canvas = document.getElementById(this.canvasId) as HTMLCanvasElement
canvas.width = this.width
canvas.height = this.height
const context = canvas.getContext('2d') as CanvasRenderingContext2D
context.fillStyle = 'white'
for (let x = 0; x < this.width; x++) {
const xp = this.real_min + (x * (this.real_max - this.real_min)) / this.width
for (let y = 0; y < this.height; y++) {
const yp = this.imaginary_max - (y * (this.imaginary_max - this.imaginary_min)) / this.height
const c = new Complex(xp, yp)
let z = Complex.zero
for (let k = 0; k < this.fractalIterationsPerPixel; k++) z = fractal(z, c)
if (z.abs() < this.boundary) context.fillRect(x, y, 1, 1)
}
}
}
/*
* Display 'Please wait...' at the center of the canvas
*
*/
pleaseWait() {
const canvas = document.getElementById(this.canvasId) as HTMLCanvasElement
canvas.width = this.width
canvas.height = this.height
const context = canvas.getContext('2d') as CanvasRenderingContext2D
context.fillStyle = 'white'
context.fillText('Please wait...', this.width / 2 - 30, this.height / 2)
}
}
因此,运行下面的代码:
const complexPlane = new ComplexPlane(300, 300, -1.5, 1.5, -1.5, 1.5, 1.5, 20, 'fractal')
const mandelbrot = (z: Complex, c: Complex) => add(multiply(z, z), c)
complexPlane.pleaseWait()
setTimeout(() => complexPlane.draw(mandelbrot), 500)
画布的fractal在哪里:id
<canvas id="fractal"></canvas>
给出以下结果:
对于那些想要更进一步的人
对于那些想要进一步了解的人,你可以探索这些:
- 牛顿分形
- 朱莉娅分形
- 其他分形
单元测试
以下是数字集的单元测试。
import * as core from '../src/set.core'
import * as common from '../src/set.common'
import * as numbers from '../src/set.numbers'
describe('Test empty set', () => {
it('should test empty set', () => {
expect(common.empty<number>()(7)).toBeFalsy()
})
})
describe('Test set all', () => {
it('should test set all', () => {
expect(common.all<number>()(7)).toBeTruthy()
})
})
describe('Test singleton set', () => {
it('should test singleton set', () => {
expect(common.singleton(0)(7)).toBeFalsy()
expect(common.singleton(7)(7)).toBeTruthy()
})
})
describe('Test even numbers set', () => {
it('should test even numbers set', () => {
expect(numbers.even(99)).toBeFalsy()
expect(numbers.even(998)).toBeTruthy()
})
})
describe('Test odd numbers set', () => {
it('should test odd numbers set', () => {
expect(numbers.odd(99)).toBeTruthy()
expect(numbers.odd(998)).toBeFalsy()
})
})
describe('Test Multiples of 3 set', () => {
it('should test Multiples of 3 set', () => {
expect(numbers.multipleOfThree(99)).toBeTruthy()
expect(numbers.multipleOfThree(998)).toBeFalsy()
})
})
describe('Test Multiples of 5 set', () => {
it('should test Multiples of 5 set', () => {
expect(numbers.multipleOfFive(15)).toBeTruthy()
expect(numbers.multipleOfFive(998)).toBeFalsy()
})
})
describe('Test Primes set', () => {
it('should test Primes set', () => {
expect(numbers.prime(2)).toBeTruthy()
expect(numbers.prime(4)).toBeFalsy()
expect(numbers.getPrime(10001)).toBe(104743)
})
})
describe('Test union', () => {
it('should test union', () => {
expect(core.union(numbers.even, numbers.odd)(7)).toBeTruthy()
})
})
describe('Test intersection', () => {
it('should test intersection', () => {
const multiplesOfThreeAndFive = core.intersection(numbers.multipleOfThree, numbers.multipleOfFive)
expect(multiplesOfThreeAndFive(15)).toBeTruthy()
expect(multiplesOfThreeAndFive(10)).toBeFalsy()
})
})
describe('Test Cartesian product', () => {
it('should test Cartesian product', () => {
const cp = core.cartesianProduct(numbers.multipleOfThree, numbers.multipleOfFive)
expect(cp(9, 15)).toBeTruthy()
expect(cp(10, 15)).toBeFalsy()
expect(cp(9, 10)).toBeTruthy()
})
})
describe('Test Complement', () => {
it('should test Complement', () => {
const c = core.complement(numbers.multipleOfThree, numbers.multipleOfFive)
expect(c(15)).toBeFalsy()
expect(c(9)).toBeTruthy()
})
})
describe('Test Symetric difference without Xor', () => {
it('should test Symetric difference without Xor', () => {
const sdWithoutXor = core.symmetricDifferenceWithoutXor(numbers.prime, numbers.even)
expect(sdWithoutXor(2)).toBeFalsy()
expect(sdWithoutXor(4)).toBeTruthy()
expect(sdWithoutXor(7)).toBeTruthy()
})
})
describe('Test Symetric difference with Xor', () => {
it('should test Symetric difference with Xor', () => {
const sdWithXor = core.symmetricDifferenceWithXor(numbers.prime, numbers.even)
expect(sdWithXor(2)).toBeFalsy()
expect(sdWithXor(4)).toBeTruthy()
expect(sdWithXor(7)).toBeTruthy()
})
})
describe('Test Contains', () => {
it('should test Contains', () => {
expect(core.contains(common.singleton(0), 7)).toBeFalsy()
expect(core.contains(common.singleton(7), 7)).toBeTruthy()
})
})
describe('Test Add', () => {
it('should test Add', () => {
expect(core.contains(common.singleton(0), 7)).toBeFalsy()
expect(core.add<number>(common.singleton(0), 7)(7)).toBeTruthy()
expect(core.add<number>(common.singleton(1), 0)(0)).toBeTruthy()
expect(core.add<number>(common.singleton(19), 0)(7)).toBeFalsy()
})
})
describe('Test Remove', () => {
it('should test Remove', () => {
expect(core.remove<number>(common.singleton(0), 0)(7)).toBeFalsy()
expect(core.remove<number>(common.singleton(7), 7)(0)).toBeFalsy()
expect(core.remove<number>(common.all<number>(), 0)(0)).toBeFalsy()
expect(core.remove<number>(common.all<number>(), 0)(7)).toBeTruthy()
})
})
使用以下命令运行单元测试后:
npm test
我们达到了 100% 的代码覆盖率。
覆盖报告写在./coverage文件夹中。
就这样!希望你喜欢阅读。
鏂囩珷鏉ユ簮锛�https://dev.to/aelassas/function-programming-in-typescript-575j 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com