Python 线性回归简介
线性回归是一种基本的预测分析技术,它利用历史数据预测输出变量。它在预测建模中很受欢迎,因为它易于理解,可以用通俗易懂的语言解释。
线性回归模型在现实世界中有许多行业应用,例如经济学(例如预测增长)、商业(例如预测产品销售、员工绩效)、社会科学(例如根据性别或种族预测政治倾向)、医疗保健(例如根据体重预测血压水平、根据生物因素预测疾病发作)等。
了解如何实现线性回归模型可以发掘数据背后的奥秘,从而解决重要的问题。我们将使用 Python,因为它是一个强大的数据处理和建模工具。它拥有一系列用于线性回归建模的软件包。
其基本思想是,如果我们能将线性回归模型拟合到观测数据中,那么我们就可以使用该模型预测任何未来值。例如,假设我们从历史数据中发现,房屋的价格(P )与其面积( S )呈线性相关——事实上,我们发现房屋的价格恰好是其面积的90倍。方程式如下:
P = 90*S
有了这个模型,我们就可以预测任何房屋的价格。如果我们有一栋面积为 1,500 平方英尺的房子,我们可以计算出它的价格为:
P = 90*1500 = 135,000 美元
在这篇博文中,我们涵盖了:
- 模型背后的基本概念和数学
- 如何使用模拟数据从头实现线性回归
- 如何使用
statsmodels - 如何使用
scikit-learn
本简短教程改编自下一个使用 Python 的 XYZ 线性回归课程,其中包括浏览器内沙盒环境、要完成的任务以及使用公共数据集的项目。
基本概念和数学
线性回归模型中有两种变量:
- 输入变量或预测变量是帮助预测输出变量值的变量。通常称为X。
- 输出变量是我们想要预测的变量。通常称为Y。
为了使用线性回归估计Y,我们假设以下方程:
Yₑ = α + β X
其中Y ₑ 是根据我们的线性方程估计或预测的Y值。
我们的目标是找到参数 α和β的统计显著值,以最小化Y和Y ₑ之间的差异。
如果我们能够确定这两个参数的最佳值,那么我们将得到最佳拟合线,可以根据X的值预测Y的值。
那么,我们如何估计α和β呢?我们可以使用一种称为普通最小二乘法的方法。
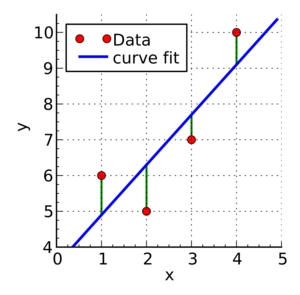
普通最小二乘法
绿线表示实际值 Y 与估计值Y之间的差异ₑ
最小二乘法的目标是找到α和β的值,使Y和Yₑ的平方差之和最小化。我们这里就不展开推导了,但利用微积分,我们可以得出未知参数的值如下:
其中X̄是X值的平均值, Ȳ是Y值的平均值。
如果您熟悉统计数据,您可能会将β简单地识别为
Cov(X, Y) / Var(X)。
从零开始的线性回归
在本文中,我们将使用两个 Python 模块:
statsmodels— 一个提供用于估计许多不同统计模型的类和函数的模块,以及用于进行统计测试和统计数据探索的模块。scikit-learn— 一个为数据挖掘和数据分析提供简单、高效工具的模块。
在深入研究之前,了解如何从头开始实现该模型非常有用。了解这些包的幕后工作原理非常重要,这样您就不会只是盲目地实现这些模型。
首先,让我们模拟一些数据,看看预测值(Yₑ)与实际值(Y)有何不同:
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# Generate 'random' data
np.random.seed(0)
X = 2.5 * np.random.randn(100) + 1.5 # Array of 100 values with mean = 1.5, stddev = 2.5
res = 0.5 * np.random.randn(100) # Generate 100 residual terms
y = 2 + 0.3 * X + res # Actual values of Y
# Create pandas dataframe to store our X and y values
df = pd.DataFrame(
{'X': X,
'y': y}
)
# Show the first five rows of our dataframe
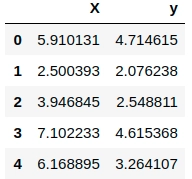
df.head()
如果运行上述代码(例如在 Jupyter 笔记本中),则会输出类似以下内容:
要使用 OLS 方法估计y,我们需要计算xmean和, X和yymean的协方差( ),以及X的方差( ),然后才能确定和的值。xycovxvaralphabeta
# Calculate the mean of X and y
xmean = np.mean(X)
ymean = np.mean(y)
# Calculate the terms needed for the numator and denominator of beta
df['xycov'] = (df['X'] - xmean) * (df['y'] - ymean)
df['xvar'] = (df['X'] - xmean)**2
# Calculate beta and alpha
beta = df['xycov'].sum() / df['xvar'].sum()
alpha = ymean - (beta * xmean)
print(f'alpha = {alpha}')
print(f'beta = {beta}')
Out:
alpha = 2.0031670124623426
beta = 0.32293968670927636
alpha太好了,我们现在对和有了估计beta!我们的模型可以写成Yₑ = 2.003 + 0.323 X,我们可以做出预测:
ypred = alpha + beta * X
Out:
array([3.91178282, 2.81064315, 3.27775989, 4.29675991, 3.99534802,
1.69857201, 3.25462968, 2.36537842, 2.40424288, 2.81907292,
...
2.16207195, 3.47451661, 2.65572718, 3.2760653 , 2.77528867,
3.05802784, 2.49605373, 3.92939769, 2.59003892, 2.81212234])
让我们将预测结果ypred与实际值进行对比y,以便更好地直观地理解我们的模型。
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(X, ypred) # regression line
plt.plot(X, y, 'ro') # scatter plot showing actual data
plt.title('Actual vs Predicted')
plt.xlabel('X')
plt.ylabel('y')
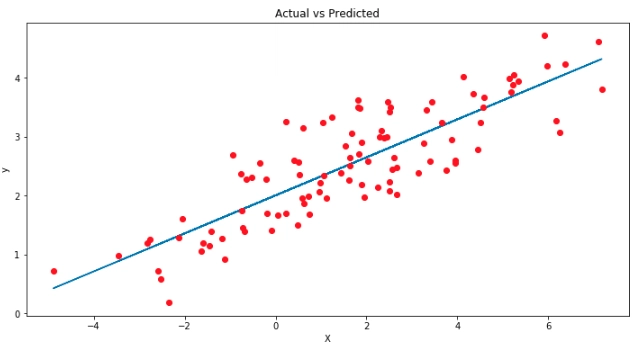
plt.show()
蓝线是我们的最佳拟合线,Yₑ = 2.003 + 0.323 X。从图中我们可以看出, X和y之间存在正线性关系。使用我们的模型,我们可以从任何X值预测y!
例如,如果我们有一个值X = 10,我们可以预测:
Yₑ = 2.003 + 0.323 (10) = 5.233。
线性回归statsmodels
现在我们已经学习了如何从头开始实现线性回归模型,我们将讨论如何使用库ols中的方法statsmodels。
为了演示此方法,我们将使用一个非常流行的advertising数据集,该数据集包含不同媒介的广告成本以及特定产品的销售额。您可以在此处下载此数据集。
在这个例子中,我们只关注TV变量——我们将探讨电视广告支出是否可以预测产品的销量。首先,我们将pandas使用以下命令将此 csv 文件导入为数据框read_csv():
# Import and display first five rows of advertising dataset
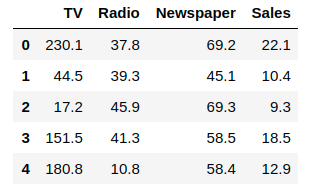
advert = pd.read_csv('advertising.csv')
advert.head()
首先,我们使用statsmodels'ols函数初始化我们的简单线性回归模型。该模型采用公式y ~ X,其中X是预测变量(TV广告成本),y是输出变量(Sales)。然后,我们通过调用 OLS 对象的方法来拟合模型fit()。
import statsmodels.formula.api as smf
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('Sales ~ TV', data=advert)
model = model.fit()
我们不再需要自己计算alpha,beta因为这个方法会自动帮我们完成!调用后model.params会显示模型的参数:
Out:
Intercept 7.032594
TV 0.047537
dtype: float64
在我们一直使用的符号中,α是截距,β是斜率,即α = 7.032 和β = 0.047。
因此,该模型的公式为:销售额 = 7.032 + 0.047*TV
用简单的英语来说,这意味着,平均而言,如果我们在电视广告上花费 100 美元,我们应该期望销售 11.73 台。
现在我们已经拟合了一个简单的回归模型,我们可以尝试根据刚刚使用该方法得出的方程来预测销售值.predict。
我们还可以通过绘制电视广告成本来可视化我们的回归模型sales_pred,以找到最佳拟合线:
# Predict values
sales_pred = model.predict()
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(advert['TV'], advert['Sales'], 'o') # scatter plot showing actual data
plt.plot(advert['TV'], sales_pred, 'r', linewidth=2) # regression line
plt.xlabel('TV Advertising Costs')
plt.ylabel('Sales')
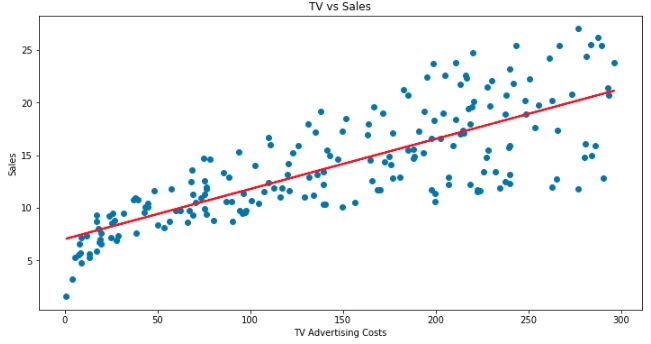
plt.title('TV vs Sales')
plt.show()
我们可以看到,电视广告成本和销售额之间存在正线性关系——换句话说,在电视广告上花费越多,销售额就越高!
使用此模型,我们可以根据电视广告支出的任何金额预测销售额。例如,如果我们将电视广告费用增加到 400 美元,我们可以预测销售额将增加到 26 个单位:
new_X = 400
model.predict({"TV": new_X})
Out:
0 26.04725
dtype: float64
线性回归scikit-learn
我们已经学会了使用...来实现线性回归模型,statsmodels现在让我们学习使用它scikit-learn!
对于此模型,我们将继续使用advertising数据集,但这次我们将使用两个预测变量来创建多元线性回归模型。这只是一个具有多个预测变量的线性回归模型,其建模方式如下:
Yₑ = α + β₁X₁ + β₂X₂ + … + β p X p,其中p是预测变量的数量。
在我们的例子中,我们将Sales使用变量进行预测TV,Radio即我们的模型可以写成:
销售额 = α + β₁*TV + β2*Radio。
首先,我们初始化线性回归模型,然后将模型拟合到我们的预测变量和输出变量:
from sklearn.linear_model import LinearRegression
# Build linear regression model using TV and Radio as predictors
# Split data into predictors X and output Y
predictors = ['TV', 'Radio']
X = advert[predictors]
y = advert['Sales']
# Initialise and fit model
lm = LinearRegression()
model = lm.fit(X, y)
同样,我们不需要自己计算alpha和的值betas——我们只需要调用.intercept_,alpha并对包含我们的系数和的.coef_数组调用:beta1beta2
print(f'alpha = {model.intercept_}')
print(f'betas = {model.coef_}')
Out:
alpha = 2.921099912405138
betas = [0.04575482 0.18799423]
因此,我们的模型可以写成:
销售额 = 2.921 + 0.046*电视 + 0.1880*广播。
我们可以通过以下方式预测值.predict():
model.predict(X)
Out:
array([20.555464, 12.345362, 12.337017, 17.617115, 13.223908,
12.512084, 11.718212, 12.105515, 3.709379, 12.551696,
...
12.454977, 8.405926, 4.478859, 18.448760, 16.4631902,
5.364512, 8.152375, 12.768048, 23.792922, 15.15754285])
现在,我们已经将多元线性回归模型拟合到数据中,可以根据电视和广播广告成本的任意组合来预测销售额!例如,如果我们想知道在电视广告上投资 300 美元,在广播广告上投资 200 美元,会有多少销售额……我们只需代入数值即可!
new_X = [[300, 200]]
print(model.predict(new_X))
Out:
[54.24638977]
这意味着,如果我们在电视广告上花费 300 美元,在广播广告上花费 200 美元,我们预计平均会售出 54 台。
我希望您喜欢这个关于线性回归基础的简短教程!
我们介绍了如何从零开始以及如何在 Python 中使用statsmodels和来实现线性回归scikit-learn。在实践中,你需要了解如何验证模型并衡量其有效性,如何为模型选择重要变量,如何处理分类变量,以及何时以及如何执行非线性变换。
 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com