fp-ts入门:函子
函数作为程序
其中约束B = F<C>导致函子
函子
函子fp-ts
一般问题解决了吗?
在上一篇关于类别的文章中,我介绍了TS类别(TypeScript 类别)以及函数组合的核心问题
我们如何组合两个通用函数
f: (a: A) => B和g: (c: C) => D?
为什么找到解决这个问题的方法如此重要?
因为如果类别可用于建模编程语言,那么态射(即TS中的函数)可用于建模程序。
因此,解决这个问题也意味着找到一种通用的程序编写方法。这对于开发人员来说非常有趣,不是吗?
函数作为程序
我们将具有以下签名的函数称为纯程序
(a: A) => B
这样的签名模拟了一个程序,该程序接受类型的输入A并产生类型的结果B,但没有任何影响。
我们将有效程序称为具有以下签名的函数
(a: A) => F<B>
这样的签名模拟了一个程序,该程序接受类型的输入A并产生类型的结果B以及效果 F,其中F是某种类型构造函数。
回想一下,类型构造函数是一个n-ary 类型运算符,以零个或多个类型作为参数,并返回另一种类型。
例子
给定具体类型string,Array类型构造函数返回具体类型Array<string>
这里我们感兴趣的是n带有 的 -ary 类型构造函数n >= 1,例如
| 类型构造函数 | 效果(解释) |
|---|---|
Array<A> |
非确定性计算 |
Option<A> |
计算可能失败 |
Task<A> |
异步计算 |
现在回到我们的主要问题
我们如何组合两个通用函数
f: (a: A) => B和g: (c: C) => D?
由于一般问题难以解决,我们需要对和施加一些约束。BC
我们已经知道,如果B = C那么解决方案就是通常的函数组合
function compose<A, B, C>(g: (b: B) => C, f: (a: A) => B): (a: A) => C {
return a => g(f(a))
}
其他情况又如何呢?
其中约束B = F<C>导致函子
让我们考虑以下约束:B = F<C>对于某些类型构造函数F,或者换句话说(经过一些重命名之后)
f: (a: A) => F<B>是一个有效的计划g: (b: B) => C是一个纯程序
为了f与组合,我们可以找到一种从一个函数提升到另一个函数的g方法,以便我们可以使用通常的函数组合(的输出类型与提升函数的输入类型相同) g(b: B) => C(fb: F<B>) => F<C>f
于是我们把原来的问题转化成了另一个问题:我们能找到这样的lift函数吗?
让我们看一些例子
例子(F = Array)
function lift<B, C>(g: (b: B) => C): (fb: Array<B>) => Array<C> {
return fb => fb.map(g)
}
例子(F = Option)
import { Option, isNone, none, some } from 'fp-ts/Option'
function lift<B, C>(g: (b: B) => C): (fb: Option<B>) => Option<C> {
return fb => (isNone(fb) ? none : some(g(fb.value)))
}
例子(F = Task)
import { Task } from 'fp-ts/Task'
function lift<B, C>(g: (b: B) => C): (fb: Task<B>) => Task<C> {
return fb => () => fb().then(g)
}
所有这些lift函数看起来几乎一模一样。这并非巧合,而是其背后的函数模式。
事实上,所有这些类型构造函数(以及许多其他类型构造函数)都允许一个函子实例。
函子
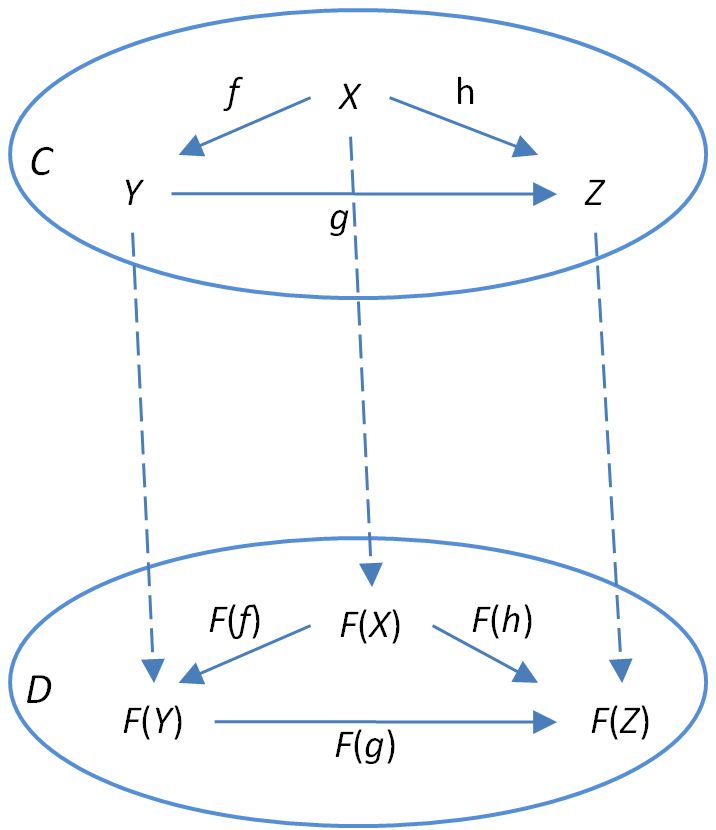
函子是类别之间的映射,它保留了类别结构,即保留了身份态射和组合。
由于范畴由两样东西(对象和态射)构成,所以函子也由两样东西构成:
- 对象之间的映射,将C
X中的每个对象与D中的对象关联起来 - 态射之间的映射,将C中的每个态射与D中的态射相关联
其中C和D是两个类别(又称两种编程语言)。
虽然两种不同编程语言之间的映射很有意思,但我们更感兴趣的是C和D重合(且符合TS)的映射。在这种情况下,我们讨论的是自函子(“endo” 表示“在……之内”、“内部”)。
从现在开始,当我写“函子”时,我实际上指的是TS中的自函子。
定义
函子是一对,(F, lift)其中
F是一个n-ary 类型构造函数(n >= 1),它将每个类型映射X到类型F<X>(对象之间的映射)lift是具有以下签名的函数
lift: <A, B>(f: (a: A) => B) => ((fa: F<A>) => F<B>)
将每个函数映射f: (a: A) => B到一个函数lift(f): (fa: F<A>) => F<B>(态射之间的映射)。
必须满足以下属性
lift(identityX)=identityF(X)(身份映射到身份)lift(g ∘ f) = lift(g) ∘ lift(f)(映射组合就是映射的组合)
该lift函数也被称为变体map,其基本上是lift重新排列参数
lift: <A, B>(f: (a: A) => B) => ((fa: F<A>) => F<B>)
map: <A, B>(fa: F<A>, f: (a: A) => B) => F<B>
请注意,map可以从中得出lift(反之亦然)。
函子fp-ts
我们如何在 中定义一个函子实例fp-ts?让我们看一个实际的例子。
以下声明定义了 API 调用响应的模型
interface Response<A> {
url: string
status: number
headers: Record<string, string>
body: A
}
请注意,该body字段是参数化的,这使得它成为Response函子实例的良好候选者,因为Response它是一个具有(必要先决条件)n的 -ary 类型构造函数。n >= 1
为了定义一个函子实例,Response我们必须定义一个map函数(以及所需的一些技术细节fp-ts)
// `Response.ts` module
import { Functor1 } from 'fp-ts/Functor'
export const URI = 'Response'
export type URI = typeof URI
declare module 'fp-ts/HKT' {
interface URItoKind<A> {
Response: Response<A>
}
}
export interface Response<A> {
url: string
status: number
headers: Record<string, string>
body: A
}
function map<A, B>(fa: Response<A>, f: (a: A) => B): Response<B> {
return { ...fa, body: f(fa.body) }
}
// functor instance for `Response`
export const functorResponse: Functor1<URI> = {
URI,
map
}
一般问题解决了吗?
完全不是。函子允许我们f用纯程序组合出一个有效程序g,但g必须是一元的,也就是说它只能接受一个参数作为输入。如果g接受两个参数呢?或者三个?
| 计划 f | 程序g | 作品 |
|---|---|---|
| 纯的 | 纯的 | g ∘ f |
| 有效的 | 纯(一元) | lift(g) ∘ f |
| 有效的 | 纯(n-ary,n > 1) |
? |
为了处理这种情况,我们需要更多的东西:在下一篇文章中,我将讨论函数式编程的另一个显著的抽象:应用函子。
TLDR:函数式编程就是组合
文章来源:https://dev.to/gcanti/getting-started-with-fp-ts-functor-36ek 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com