独特的 JavaScript 面试挑战
大家好吗?欢迎回到“代码评审”系列,这是一系列每周在 Dev.to 独家发布的编程面试挑战和职业相关内容。我是伊丽莎白·格罗斯 (Elisabeth Gross),你可能因为我在Coderbyte的工作而认识我,Coderbyte 是一个致力于帮助各级开发人员获得下一份工程工作的网站。或者,你可能通过Breadwinnerss听说过我,Breadwinnerss 是一个帮助用户在数十家公司中申请他们感兴趣的职位的介绍的工具。
撰写本系列文章最棒的部分,就是认识了你们,你们都是一群充满干劲和热情的开发者,对提升编程技能充满热情。如果你想了解更多技巧和窍门,以及一些开发者的生活方式内容,请在 Instagram 上关注我 @elisabethgross568。我会分享我在纽约最喜欢去的咖啡店、我最喜欢在编程时听的一些播放列表等等!我迫不及待地想和你们进行更多交流。好了,闲话少叙——让我们开始讨论上周挑战的解决方案吧。
解决方案
这个解决方案可以计算出水平面上可以容纳多少水,然后将各层相加得到总体积。在每一层水平面上,我们可以找到峰值,也就是水可以存在的边界,然后减去每个峰值的索引,得到它们之间可以容纳水的空间。用代码来直观地展示这一点可能更容易!
专业提示
这个问题是构建一些辅助函数的绝佳机会。通常,在解决一个包含很多内容的算法难题时,从更通用的概念入手会很有帮助,并在面试过程中不断完善辅助函数。这可以向面试官传达两点:首先,你理解了问题的总体概念,并可以为自己构建一个由构成难题的较小模块组成的迷你路线图,这些模块最终将成为你的算法。其次,你不会被细节所困扰。我面试的时候,很多时候面试官一开始就被算法的一小部分所困扰,而没有深入到算法的真正核心。通过辅助函数,你可以立即专注于基本结构,然后利用剩下的时间完善这些辅助函数。
function totalWaterVolume(arr) {
// first, we find the 'maxHeight’ which is the highest peak in the water collector
const maxHeight = Math.max(...arr)
let totalVolume = 0
// this loop starts at the maxHeight then decrements the height
for (let horizontalLevel = maxHeight; horizontalLevel > 0; horizontalLevel--) {
// 'peaksAtHorizontalLevel' is set to the return value of our first helper function 'peakIndicesMaker' which will be an array of indices of rain collector walls that exist at that level
var peaksAtHeightLevel = peakIndicesMaker(arr, horizontalLevel)
// 'vol' is then incremented by the volume that exists at that level, returned from our second helper function 'volAtLevel'
totalVolume += volAtLevel(peaksAtHeightLevel)
}
// total volume is returned
return totalVolume
}
让我们看一个例子来帮助说明我们目前所拥有的内容。
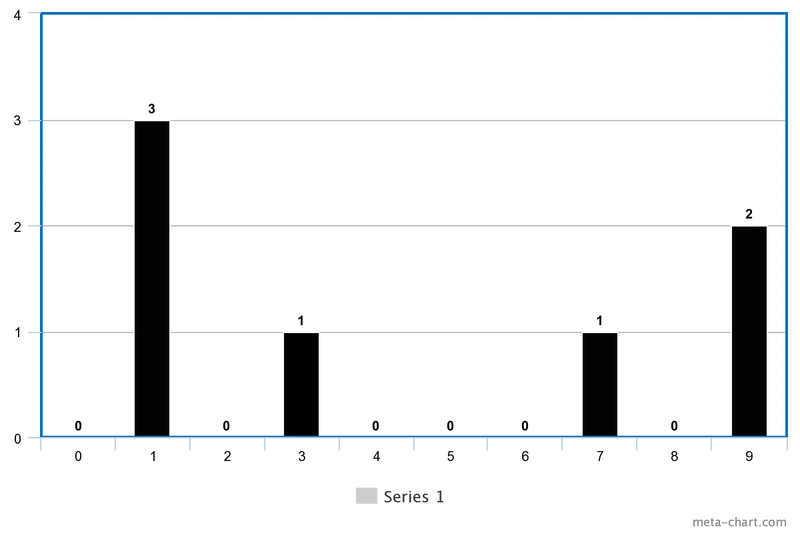
给定数组 [0, 3, 0, 1, 0, 0, 0, 1, 0, 2],我们的雨水收集器将如下所示-
首先,我们获取maxHeight,在本例中为 3 。我们将从 3 开始循环遍历每个水平层级。
让我们开始构建peakIndicesMaker函数吧!记住,这个函数应该返回雨水收集器每个水平层的峰值。
/* This function takes the original array, as well as the height level we are looking at, and returns an array of indices where reservoir walls exist */
function peakIndicesMaker(arr, level) {
const peakIndices = []
// loop over the entire array
for (let i = 0; i < arr.length; i++) {
// if the wall height present at each index is at least the height of the given level then that index is pushed to the output array
if(arr[i] >= level) {
peakIndices.push(i)
}
}
// array of indices is returned
return peakIndices
}
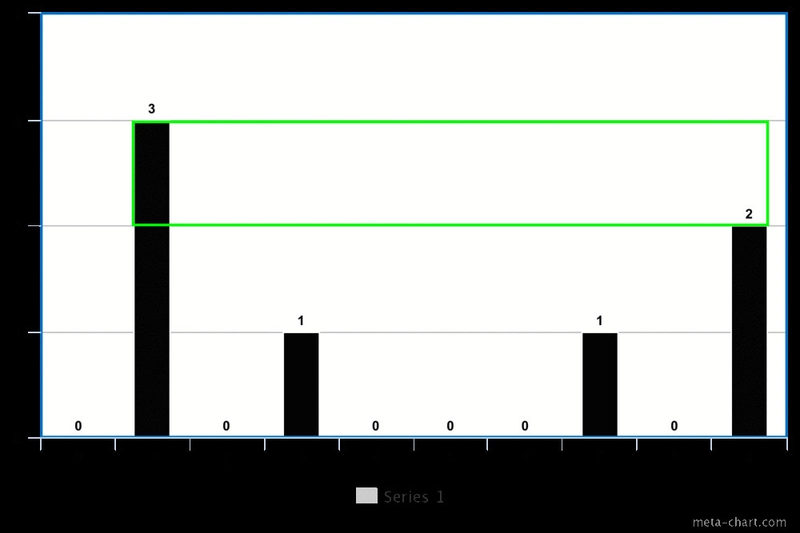
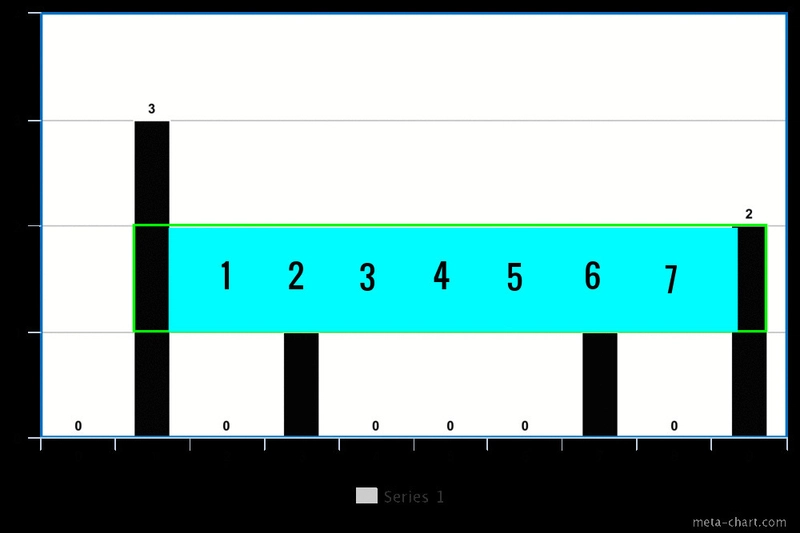
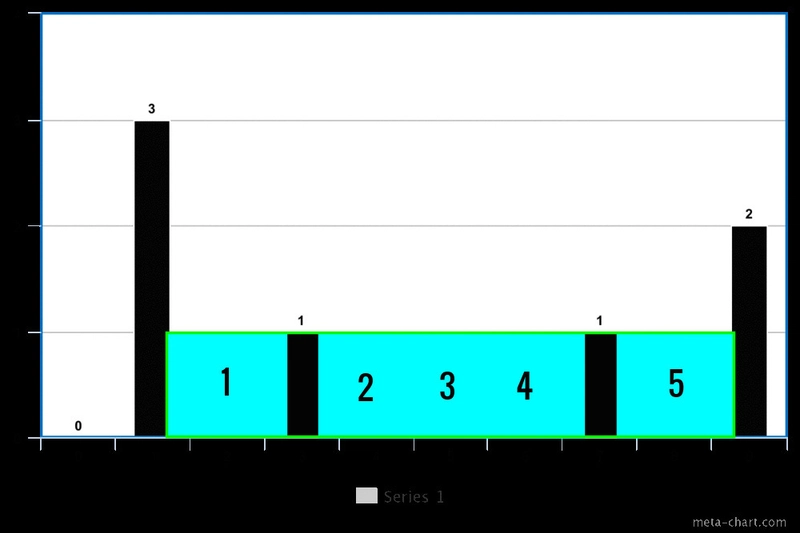
对于我们的示例,级别 3 将返回[1](索引 1 处仅一个峰值),级别 2 将返回[1, 9](索引 1 和 9 处两个峰值),级别 1 将返回[1, 3, 7, 9](索引 1、3、7 和 9 处四个峰值)。
获取每个层级的峰值索引,我们就能找到它们之间的距离,最终计算出那里会聚集多少水!让我们看看代码里是怎么实现的。
/* The distance between the two walls at the same height will also be the volume of water held between them. */
function volAtLevel(peakIndices) {
let levelVol = 0
// if there is only one wall at the height currently being calculated, there cannot physically be any water at that level. In this case, we return 0 volume.
if (peakIndices.length === 1) {
return 0
} else {
// levelVol is incremented for each 'pair' of walls at that level. It is important to note that we are comparing each wall to its adjacent neighbor located at the next index in the array. Therefore the last element in the array could not possibly hold water to its right. This is because no wall exists at that level beyond the last wall
for (let i = 0; i < peakIndices.length-1; i++) {
// Measure the right side of one wall (this is why we look at peakIndices[i] + 1 and not just peakIndices[i]) to the left side of its neighbor
levelVol += (peakIndices[i + 1] - (peakIndices[i] + 1))
}
}
// the level volume is then returned after all pairs have been summed.
return levelVol
}
对于我们的例子,在第一个水平级别(高度 = 3),我们返回 0,因为只有一个峰值索引。
对于下一级(高度 = 2),我们有两个峰值 [1, 9]。我们从 9(第二个峰值的索引)中减去 2(第一个峰值的索引加 1),得到 7。
对于下一级(高度 = 1),我们有 4 个峰 [1, 3, 7, 9]。我们从 3(第二个峰的索引)中减去 2(第一个峰的索引加 1),得到 1。然后,我们从 7(第三个峰的索引)中减去 4(第二个峰的索引加 1),得到 3。最后,我们从 9(第四个峰的索引)中减去 8(第三个峰的索引加 1),得到 1。
总体积将是每层体积的总和,在本例中为 12。就是这样!希望你和我一样喜欢这个问题 :) 下周见!
鏂囩珷鏉ユ簮锛�https://dev.to/coderbyte/a-unique-javascript-interview-challenge-538e 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com