理解二叉搜索树 二叉树和二叉搜索树

2025-06-04

理解二叉搜索树

二叉树和二叉搜索树

正如我在上一篇关于递归的文章中所承诺的（我建议在阅读本文之前先阅读那篇，因为我们会在示例中大量使用递归），我想在本文中更深入地探讨一下树形数据结构。树是一种非顺序数据结构，可用于存储需要轻松查找的信息。换句话说，它们是层级结构的抽象模型（想象一下家谱）。树由具有父子关系的节点组成。

带有标记部分的二叉树示例

二叉树和二叉搜索树

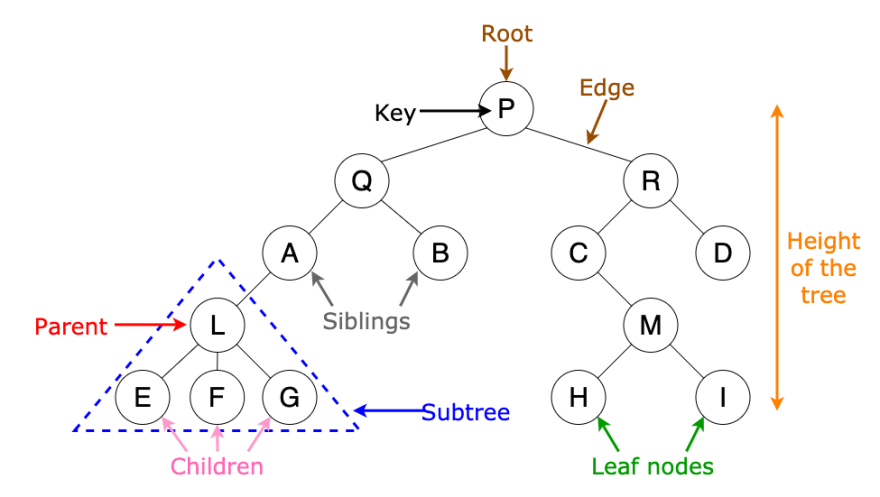
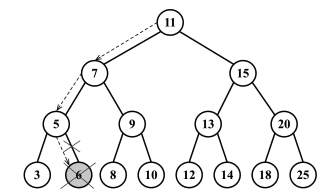
二叉树中的每个节点最多有两个子节点：左子节点和右子节点。此定义允许你编写算法来更高效地插入、查找和删除节点。请参阅上图，了解二叉树以及我将在本文中使用的关键词汇。

二叉搜索树的例子

你可能已经猜到了，二叉搜索树 (BST)就是一棵二叉树。关键区别在于，BST 只允许将值较小的节点存储在左侧，将值较大的节点存储在右侧。如果你​​没注意到，上图就很好地说明了这一点。如果你难以理解这幅图的排序方式，别担心，我们将在下一节中更详细地讲解！

创建 Node 和 BST 类

和往常一样，我非常鼓励你和我一起写代码，并不断测试/实践我们写的任何代码。首先，我们将创建一个Node类来表示二叉搜索树中的节点：

class Node {
    constructor(data) {
        this.data = data; // node value
        this.left = null;   // left node child reference
        this.right = null; // right node child reference
    }
}

接下来，我们将声明类的基本结构BinarySearchTree：

class BinarySearchTree {
    constructor() {
        this.root = null; // root of bst
    }
}

下一步我们将实现一些方法。以下是我们将要介绍的内容：

  • insert(data)
  • inOrderTraverse()
  • preOrderTraverse()
  • postOrderTraverse()
  • search(data)
  • remove(data)

将节点插入到 BST 中

要将新节点插入树，我们将遵循两个步骤：

  1. 验证插入操作是否为特殊情况。换句话说，我们需要检查要添加的节点是否是树中的第一个节点。如果是，我们只需root创建该类的实例并将Node其赋值给该root属性，使其指向这个新节点即可。
  2. 将节点添加到与 不同的位置root。
insert(data) {
    let newNode = new Node(data);

    if(this.root === null) {
        this.root = newNode;
    } else {
        this.insertNode(this.root, newNode); // helper method below
    }
}

insertNode(node, newNode) {
    if(newNode.data < node.data) {
        if(node.left === null) {
            node.left = newNode;
        } else {
            this.insertNode(node.left, newNode);
        }
    } else {
        if(node.right === null) {
            node.right = newNode;
        } else {
            this.insertNode(node.right, newNode);
        }
    }
}

总而言之，insert(data)创建一个新的Node值为 的节点data，如果树为空，则将该节点设置为树的root，否则调用insertNode(this.root, newNode)。insertNode (node, newNode)是我们的辅助方法，负责将新节点数据与当前节点的数据进行比较，并相应地递归地向左或向右移动，直到找到一个具有空值的正确节点，可以在该节点处添加新节点。

例如，如果我们要执行以下代码...

const BST = new BinarySearchTree();
BST.insert(11); // establishes root node 
BST.insert(7);
BST.insert(9);
BST.insert(15);
...
BST.insert(6);

...我们可以用这张图来说明最后的插入：
将 6 插入二叉搜索树

遍历 BST

遍历树是访问树中所有节点并在每个节点上执行操作的过程。最大的问题是，我们应该如何进行遍历？有三种常见的方法：中序遍历、前序遍历和后序遍历。

中序遍历

中序遍历将从给定节点（可选）开始，按升序访问所有节点，并执行给定的回调函数（同样可选）。同样，我们将在这里使用递归：

inOrderTraverse(node, callback) {
    if(node != null) {
        this.inOrderTraverse(node.left, callback);
        callback(node.data);
        this.inOrderTraverse(node.right, callback);
    }
}

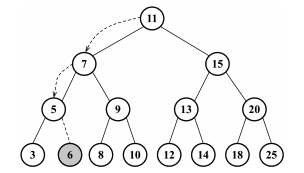
下图显示了我们所采取的路径inOrderTraverse：

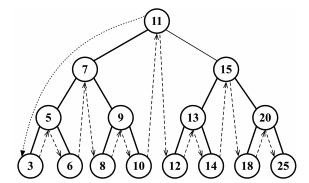
二叉搜索树的中序遍历

前序遍历

前序遍历会先访问该节点，然后再访问其后代节点。请注意代码和图中顺序的细微差别：

preOrderTraverse(node, callback) {
    if(node != null) {
        callback(node.data);
        this.preOrderTraverse(node.left, callback);
        this.preOrderTraverse(node.right, callback);
    }
}

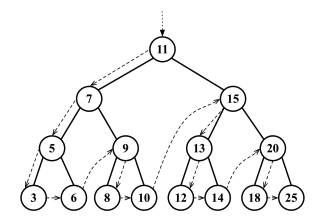
二叉搜索树的前序遍历

后序遍历

如果你还没猜到，后序遍历会先访问该节点的后代节点。你大概能猜到代码会有什么不同，但一定要对照图表仔细检查：

postOrderTraverse(node, callback) {
    if(node != null) {
        this.postOrderTraverse(node.left, callback);
        this.postOrderTraverse(node.right, callback);
        callback(node.data);
    }
}

二叉搜索树的后序遍历

在 BST 中搜索值

在我们的实现中，node表示当前节点，数据表示我们正在搜索的值：

search(node, data) {
    if(node === null) {
        return null;
    } else if(data < node.data) {
        return this.search(node.left, data);
    } else if(data > node.data) {
        return this.search(node.right, data);
    } else {
        return node;
    }
}

我鼓励你在这里测试一下你的代码，你可以添加一个 console.log 来查看哪些节点被访问了。即使你没有参与编程，也可以继续跟踪本文中的某个图表，并预测该方法在搜索特定值时的路径。你会发现查找最大值和最小值也非常简单！

从 BST 中删除节点

该remove方法是我们在本文中介绍的最复杂的方法。它的复杂性在于我们需要处理不同的场景，并且它是递归的。

remove(data) {
    this.root = this.removeNode(this.root, data); // helper method below
}

removeNode(node, data) {
    if(node === null) {
        return null;
    // if data to be deleted is less than the root's data, move to the left subtree
    } else if(data < node.data) {
        node.left = this.removeNode(node.left, data);
        return node;
    // if data to be deleted is greater than the root's data, move to the right subtree
    } else if(data > node.data) {
        node.right = this.removeNode(node.right, data);
        return node;
    // if data is similar to the root's data, delete the node
    } else {
        // delete node with no children (leaf node)
        if(node.left === null && node.right === null) {
            node = null;
            return node;
        }

        // delete node with one child
        if(node.left === null) {
            node = node.right;
            return node;
        } else if(node.right === null) {
            node = node.left;
            return node;
        }

        // delete node with two children
        // minimum node of the right subtree is stored in newNode
        let newNode = this.minNode(node.right);
        node.data = newNode.data;
        node.right = this.removeNode(node.right, newNode.data);
        return node;
    }
}

如果我们最终找到了要删除的匹配节点，则需要处理三种情况，我们将在下面详细讨论。这些情况可以在代码中的 else 语句中找到。

删除叶节点

第一种情况涉及一个没有左子节点或右子节点的叶节点。在这种情况下，我们需要通过赋值操作来移除该节点null。但是，别忘了，我们还需要处理来自父节点的引用。请参阅移除叶节点的示意图：

从二叉搜索树中删除叶节点

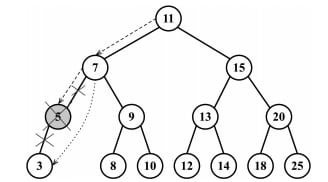
删除具有一个子节点的节点

第二种情况涉及一个具有左或右子节点的节点。如下图所示，我们需要跳过匹配节点，并将父指针赋给子节点：

删除二叉搜索树中具有左孩子的节点

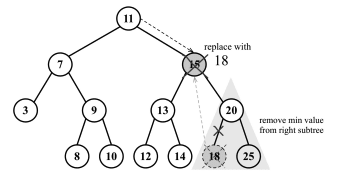
删除具有两个子节点的节点

第三个也是最后一个场景涉及一个同时具有 let 和 right 子节点的节点。要删除这样的节点，请按照以下步骤操作：

  1. 找到要删除的节点后，从其右边子树中找到最小节点（参考下图中的阴影区域）。
  2. 接下来，你可以用该节点右子树中最小节点的键来更新该节点的值。此操作实际上是替换了该节点的键，这意味着该节点实际上已被删除。
  3. 现在树中有两个节点具有相同的键，这不可能发生（参见图中的两个 18）。因此，你需要从右子树中删除最小节点，因为你已将其移动到被删除节点的位置。
  4. 最后，将更新后的节点引用返回给其父节点。

从二叉搜索树中删除具有两个子节点的节点

结论

在本文中，我们介绍了在二叉搜索树中添加、搜索和删除节点以及树遍历的算法。

为了增加一些乐趣，我偶然发现了一个有趣的工具，你可以用它来操作交互式二叉树以及许多其他数据结构，它是由 David Galles 创建的。如果你想了解更多关于封面图片以及它与二叉树的关系，可以看看 Larry Riddle 对对称二叉树的解释（注意，它涉及的数学知识比较多，但有一些很酷的插图）！

文章来源：https://dev.to/christinamcmahon/understanding-binary-search-trees-4d90
Devto 翻译
PREV
迭代数组的 7 种方法以及每种方法的适用场景
NEXT
递归解释（附示例）