使用 JavaScript 理解 Big-O 符号

大 0 符号入门

O(1) 是神圣的。 ~Hamid Tizhoosh

大 O 符号衡量算法的最坏情况复杂度。在大 O
符号中，n 表示输入的数量。用大 O 符号提出的问题是
：“当 n 趋近于无穷大时会发生什么？”

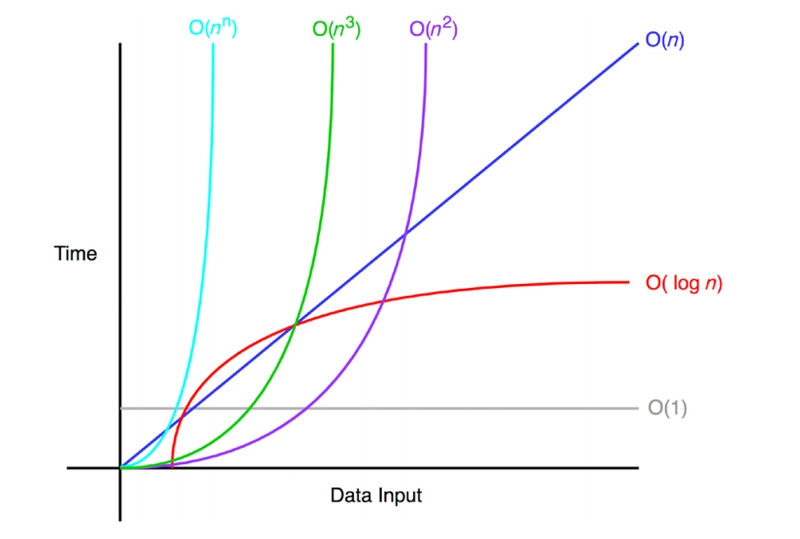
下图展示了一些常见的 Big-O 符号：

恒定时间（O(1)）

O(1) 不会随输入空间而变化。因此，O(1) 被称为常数时间。O
(1) 的示例如下：

function exampleConstantFunc(n) {
    return n*n;
}

线性时间（O（n））

O(n) 是线性时间复杂度，适用于在最坏情况下必须执行n 个
操作的算法。它通常只是一个简单的基本循环，在其中执行常数时间操作。O
(n) 的示例如下：

function exampleLinear(n) {
    for (var i = 0 ; i < n; i++ ) {
        console.log(i)
    }
}

对数时间 O(log(n))

对数时间函数是指执行时间与输入大小的对数成正比的函数。
请考虑以下示例：

function log(n) {
    for (let i = 1; i < n; i*=2) {
        const result = i;
        console.log(result);  
    }
}

我们可以看到，在任何给定的迭代中，i 的值 = 2i，因此在第 n 次迭代中，i 的值 = 2n。此外，我们知道 i 的值始终小于循环本身的大小（N）。
由此，我们可以推导出以下结果：
2^n < N
log(2^n) < log(N)
n < log(N)

从上面的代码可以看出，迭代次数始终小于输入大小的对数。因此，该算法的最坏时间复杂度为 O(log(n))。对
数时间复杂度的效率在处理诸如一百万个条目这样的大输入时尤为明显。

二次时间(O(n^2))

有了二次时间算法，我们现在已经进入了时间复杂度的黑暗面。
顾名思义，输入的大小会二次方地影响算法的运行时间。一个常见的例子是嵌套循环：

for (int i = 0; i <n; i += c) {
    for (int j = 0; j < n; j += c) {
    // some O(1) expressions
    }
}

从前面的例子可以看出，当 i = 0 时，内循环运行 n 次，当 i = 1 和 i = 2 时，内循环也运行 n 次，以此类推。内循环总是运行 n 次，并且与 n 的值无关，因此算法的时间复杂度为 O(n² ⁾。

多项式时间(O(n ⁿ ))

多项式时间复杂度是指算法的运行时间复杂度，其运行次数为 n ^k阶。二次时间算法是某些类型的多项式时间算法，其中 k = 2。此类算法的一个非常简单的示例如下：


for (int i = 0; i <n; i += c) {
    for (int j = 0; j < n; j += c) {
        for (int k = 0; k < n; k += c) {
            // some O(1) expressions
        }
    }
}

如您所见，此示例只是二次时间部分中示例的扩展。此示例的最坏情况复杂度为 O(n ³ )。
如您所见，此示例只是二次时间
部分中示例的扩展。此示例的最坏情况复杂度为 O(n ³ )。

大O符号规则

我们将算法的复杂度表示为 f(n)。n 表示输入的数量，f(n)time 表示所需时间，f(n)space 表示算法所需的空间（额外内存）。算法分析的目标是通过计算 f(n) 来了解算法的效率。
然而，计算 f(n) 可能颇具挑战性。大 O 符号提供了一些基本规则，帮助开发人员计算 f(n)。

系数规则：“去掉常数”

我们先来回顾一下系数规则。这条规则是最容易理解的。它只要求你忽略任何与输入大小无关的常量。在 Big-O 中，当输入规模较大时，系数可以忽略不计。因此，这是 Big-O 符号中最重要的规则。

如果 f(n) 是 O(g(n))，那么对于任何常数 k > 0，kf(n) 也是 O(g(n))。

这意味着 5f(n) 和 f(n) 都具有相同的大 O 符号 O(f(n))。
以下是时间复杂度为 O(n) 的代码块示例：

function a(n){
    var count =0;
    for (var i=0;i<n;i++){
        count+=1;
    }
    return count;
}

这段代码的 f(n) = n。这是因为它对 count 进行了 n 次加法运算。因此，该函数的时间复杂度为 O(n)。

function a(n){
    var count =0;
    for (var i=0;i<5*n;i++){
        count+=1;
    }
    return count;
}

这个块的 f(n) = 5n。这是因为它从 0 运行到 5n。
然而，前两个示例都使用大 O 符号 O(n)。简而言之，这是因为如果 n 接近无穷大或其他大数，那么这四个额外的操作就毫无意义。
它会执行 n 次。在大 O 符号中，任何常量都可以忽略不计。

求和规则：“将大写字母 O 加起来”

求和规则很容易理解；时间复杂度可以相加。想象一下，一个主算法包含两个其他算法。该主算法的大 O 符号就是另外两个大 O 符号之和。

如果 f(n) 是 O(h(n)) 且 g(n) 是 O(p(n))，则 f(n)+g(n) 是 O(h(n)+p(n))。

记住在应用此规则后应用系数规则非常重要。
以下代码块演示了一个包含两个主循环的函数，其时间复杂度必须分别考虑，然后相加：

function a(n){
    var count =0;
    for (var i=0; i<n; i++){
        count+=1;
    }
    for (var i=0; i<5*n; i++){
        count+=1;
    }
    return count;
}

在这个例子中，第 4 行 f(n) = n，第 7 行 f(n) = 5n。结果是 6n。
然而，应用系数规则时，最终结果是 O(n) = n。

乘积规则：“乘以大 O”

乘积规则简单地说明了如何将 Big-O 相乘。

如果 f(n) 为 O(h(n))，g(n) 为 O(p(n))，则 f(n)g(n) 为 O(h(n)p(n))。
以下代码块演示了一个具有两个嵌套 for 循环的函数，其中应用了乘积规则：

function (n){
    var count =0;
    for (var i=0; i<n; i++){
        count+=1;
        for (var i=0; i<5*n; i++){
            count+=1;
        }
    }
    return count;
}

在此示例中，f(n) = 5n*n，因为第 7 行运行了 5n 次，总共进行了 n 次迭代。
因此，总共进行了 5n^ ^{2 次}运算。应用系数规则，结果为 O(n)=n ^{^2}

多项式规则：“大O的k次方”

多项式规则指出，多项式时间复杂度具有与多项式次数相同的大O符号。
从数学上讲，它如下所示：

如果 f(n) 是 k 次多项式，则 f(n) 为 O(n ^k )。
以下代码块只有一个 for 循环，时间复杂度为二次方：

function a(n){

    var count =0;

    for (var i=0; i<n*n; i++){
        count+=1;
    }
    return count;
}

在此示例中，f(n) = n ^2，因为第 4 行运行 n*n 次迭代。

多项式时间复杂度类

既然我们已经开始了讨论，那么到目前为止，我们讨论的大多数时间复杂度类型都是 O(n ^k ) 类型，例如，当 n = 1 时，它是常数时间复杂度，而当 k = 2 时，它是二次复杂度。
多项式时间复杂度的概念将我们引向一类问题，这些问题是根据其解的复杂性定义的。以下是这些类的类型：

P：任何可以在多项式时间 O(n ^k ) 内解决的问题。
NP：任何可以在多项式时间内验证的问题。有些问题（例如数独求解）可以在非确定性多项式时间内解决。如果这些问题的解可以在多项式时间内验证，则该问题被归类为 NP 类问题。NP 类问题是 P 类问题的超集。
NP完全问题：任何可以在多项式时间内归结为另一个NP问题的函数的NP问题，都可以归类为NP完全问题。这意味着，如果我们知道某个NP问题的解，那么就可以在多项式时间内推导出另一个NP问题的解。
NP-Hard：如果存在一个可以在多项式时间内简化为 H 的 NP-Complete 问题 (C)，则可以将问题归类为 NP-Hard 问题 (H)。

在大多数现实世界中，我们会遇到大量的P类和NP类问题，NP类问题的一个典型例子是旅行推销员问题。一个推销员希望从他家出发，访问n个城市作为行程的起点和终点。由于汽油数量有限，且行驶里程有上限，这位推销员能否在不耗尽汽油的情况下访问所有城市？

递归和加法复杂性

到目前为止，我们已经看到了一些非常简单的例子：它们都包含单个循环或嵌套循环。然而，很多时候，我们需要处理来自同一算法的多个循环/函数调用/分支。
让我们看一个例子来说明在这种情况下如何计算复杂度。

当我们有后续循环/函数调用时，我们需要计算每个步骤的单独复杂度，然后将它们相加以获得整体复杂度，如下所示：

 function xyz() {
    abc(); // O(n) operation
    pqr(); // O(log(n)) operation
 }

这段代码的总体复杂度将是两个部分复杂度的总和。因此，在这种情况下，总复杂度将为 O(n + log n)，渐近地为 O(n)。

当我们的函数中存在具有不同时间复杂度的分支时，根据我们所讨论的运行时复杂度类型，我们需要做出正确的选择：

 function xyz() {
    if (someCondition) {
        abc(); // O(n) operation
    } else {
        pqr(); // O(log(n)) operation
    }
 }

在这种情况下，最坏情况的复杂度将由两个分支中最差的一个决定，即 O(n)，但最佳情况的复杂度将是 O(log(n))。

与非递归算法相比，递归算法有点棘手，因为我们不仅需要确定算法的复杂性，还需要记住递归会被触发的次数，因为这会增加算法的整体复杂性，如下面的代码片段所示：

 function rec1(array) {
    // O(1) operations
    if (array.length === 0) return;
    array.pop();
    return rec1(array);
 }

虽然我们的方法只执行了一些 O(1) 操作，但它会不断更改输入并调用自身，直到输入数组的大小为零。因此，我们的方法最终执行了 n 次，使得总时间复杂度为 O(n)。

文章来源：https://dev.to/b0nbon1/understanding-big-o-notation-with-javascript-25mc

使用 JavaScript Big-0 Notation Primer 理解 Big-O Notation

使用 JavaScript 理解 Big-O 符号

大 0 符号入门

大 0 符号入门

恒定时间（O(1)）

线性时间（O（n））

对数时间 O(log(n))

二次时间(O(n^2))

多项式时间(O(n n ))

大O符号规则

系数规则：“去掉常数”

求和规则：“将大写字母 O 加起来”

乘积规则：“乘以大 O”

多项式规则：“大O的k次方”

多项式时间复杂度类

递归和加法复杂性

多项式时间(O(n ⁿ ))