O(log n) 是什么?学习大 O 对数时间复杂度
有没有比大 O 符号更可怕的计算机科学主题?别被它的名字吓到,大 O 符号其实没什么大不了的。它很容易理解,你不需要是数学高手就能理解。在本教程中,你将通过 JavaScript 示例学习大 O 对数时间复杂度的基础知识。
这是大 O 符号系列文章的第四篇。如果您想随时了解最新动态,请订阅我的每周简报“解决方案”。
Big O 解决了什么问题?
-
大 O 符号帮助我们回答这个问题:“它会扩展吗?”
-
Big O 符号为我们提供了一种与其他开发人员(和数学家!)讨论性能的共享语言。
快速复习
如果您刚刚加入我们,您将需要从那篇文章开始阅读,什么是大 O 符号?
什么是 Big O?
大 O 符号是一种用于测量算法增长率的系统。大 O 符号从时间和空间的角度以数学方式描述算法的复杂度。我们不会用秒(或分钟!)来衡量算法的速度。相反,我们会测量完成算法所需的操作数。O
是“Order of”(阶数)的缩写。因此,如果我们讨论的是 O(log N) 的算法,我们会说它的阶数或增长率是“log n”,即对数复杂度。
Big O 如何工作?
大 O 符号衡量最坏的情况。
为什么?
因为我们不知道我们不知道什么。
我们需要知道我们的算法表现得有多差,这样我们才能评估其他解决方案。
最坏情况也称为上限。当我们说上限时,我们指的是算法执行的最大操作数。
还记得这张桌子吗?
| 哦 | 复杂 | 增长率 |
|---|---|---|
| O(1) | 持续的 | 快速地 |
| O(log n) | 对数 | |
| 在) | 线性时间 | |
| O(n * log n) | 对数线性 | |
| O(n^2) | 二次函数 | |
| O(n^3) | 立方体 | |
| O(2^n) | 指数 | |
| 在!) | 阶乘 | 慢的 |
它按照生长速度从快到慢列出了常见的订单。
我们在什么是 Big O?中学习了 O(1),即常数时间复杂度,在Big O 线性时间复杂度中学习了 O(n) ,在Big O 二次时间复杂度中学习了 O(n^2) 。
我们之前跳过了 O(log n),对数复杂度,因为在学习了 O(n^2),二次时间复杂度之后,它会更容易理解。
现在是时候了!
数学钟🧮🕝
什么是对数?
对数使我们能够对幂进行逆向工程。(就像氪石一样!)它们是指数运算的逆运算。
我们可以把对数看作是指数运算的逆运算。还记得标准化测试中的这个类比格式吗?
A 与 B 的关系相当于 X 与 Y 的关系。
我们可以说,“加法之于减法,就如同指数之于对数。”
我们也可以说,“乘法之于除法,就如同指数之于对数。”
通过二次时间复杂度,我们得知n * n等于n^2。
如果n的值为2,那么n^2等于 4。
因此,2 的三次方2^3等于 8。
以“长”形式来看,它看起来像:
2 * 2 * 2 = 8
如果我们遇到这个问题该怎么办?
2^y = 8
您会如何描述这个问题?
我们可以说,“将 2 的幂乘以 8 得到多少次方?”
🧐
我们也可以问:“需要多少个 2 相乘才能得到 8?”
该方程的符号为:
log2(8) = y
其中2是底数,8是自变量,y是指数或幂。
为什么会有8争论? (看看我做了什么?)
因为 log2() 是一个函数!
🤯
我们可以将乘积描述为“8 的以 2 为底的对数是 3”。
我们所说的基础是什么意思?
与对数有关的三个最常见的底数是:
- 2
- 10
- e
在数字电子学和计算机科学中,我们(几乎总是)使用以2为基数,或二进制数字系统。
在二进制中,我们用两个符号进行计数:0 和 1。
眼熟?
这是布尔值!👻
除非你生来每只手就有六根手指,否则你就是以十进制或十进制数字系统来计数的。
10^2 = 100
10^3 = 1000
etc.
如果你真的想深入了解,你可以阅读e,即欧拉常数:自然对数等于一的唯一数字。
☝️ 对数不是平方根。
8 的平方根是 2.82842712475。
8 的 log2 是 3。
这里的区别很小,但如果我们的争论增加了怎么办?
2048 的平方根是 45.2548339959。
2048 的 log2 是 11。
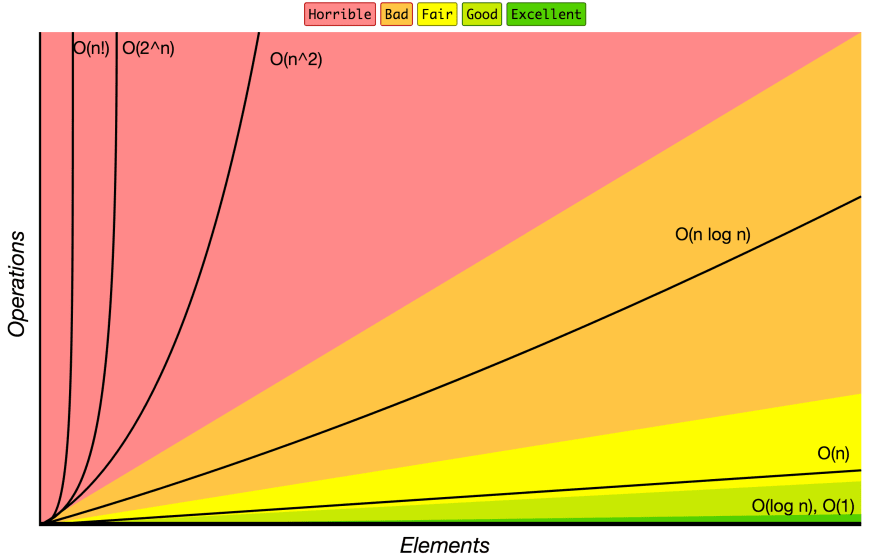
如果我们绘制对数图会怎么样?
空气动力学!
如果我们将对数时间复杂度与无处不在的 Big O 备忘单上的其他时间复杂度进行比较,我们会看到什么?
我们可以看到,对数时间复杂度非常好!
如果问题是“多少个 3 相乘才能得到 8?”
答案是 1.8927892607
如果您认为手工计算这个数字是一个繁琐的过程,那么您是对的。
这就是我们发明计算尺和精密计算器的原因。
幸运的是,我们不需要计算函数的精确对数。
通过 Big O,我们可以抽象出细节。
我们不关心我们的算法的具体实现。
我们对算法的顺序很感兴趣,这样我们就可以进行比较并评估替代解决方案。
我们认为对数的底数是一个常数,因此我们将其删除,并简单地使用以下符号:
O(log n)
O(log n):二分查找
用于说明 O(log n) 的经典示例是二分查找。二分查找是一种通过在每次迭代中将输入除以二来查找参数在已排序序列中的位置的算法。
假设我们得到以下数组并要求找到数字的位置512:
const powers = [1, 2, 4, 8 ,16, 32, 64, 128, 256, 512];
首先,我们来回顾一下这个问题的强力解决方案。
const bruteSearch = (arr, num) => {
for (let i = 0; i < arr.length; i++) {
if (arr[i] === num) {
return `Found ${num} at ${i}`;
}
}
}
i让我们将和的值映射arr[i]到数组 J4F 中:
| 我 | 数组[i] |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 三十二 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
的大 O 是什么bruteSearch()?
在)
为了找到num,我们需要检查数组中的每个项目,因此时间复杂度是线性的。
我们可以做得更好吗?
确实。
这个函数中发生了什么?
const powers = [1, 2, 4, 8 ,16, 32, 64, 128, 256, 512];
const binarySearch = (arr, num) => {
let startIndex = 0;
let endIndex = (arr.length)-1;
while (startIndex <= endIndex){
let pivot = Math.floor((startIndex + endIndex)/2);
if (arr[pivot] === num){
return `Found ${num} at ${pivot}`;
} else if (arr[pivot] < num){
startIndex = pivot + 1;
} else {
endIndex = pivot - 1;
}
}
return false;
}
在循环的第一次迭代中,我们在数组的中位数处while创建一个枢轴num。然后,我们将其与索引为 的数组中的值进行检查pivot。
如果pivot等于num,则返回。
如果pivot小于num,我们将我们的值更改startIndex为我们的值pivot加一。
为什么?
如果的值arr[pivot]小于num,我们不需要pivot在下一次迭代中检查我们下面的任何元素。
我们的投入刚刚减半!
n / 2
如果pivot大于num,我们将我们的值更改endIndex为我们的值pivot减一。
如果的值array[pivot]大于num,我们不需要pivot在下一次迭代中检查我们上方的任何元素。
在下一次迭代中,我们在调整后的和pivot之间的中位数处创建一个新的,然后再次检查的值与的值。startIndexendIndexarr[pivot]num
在上面的例子中,我们再次将输入减半。
一半的一半是什么?
四分之一。
n / 4
在第三次迭代中,我们再次将输入减半:n / 8
在最后一次迭代中,我们找到了我们的数字。此时,也没有什么可以减半了。
模式是怎样的?
我们来做一张桌子吧!
| 起始索引 | 结束索引 | 枢 | # 元素 | n |
|---|---|---|---|---|
| 0 | 9 | 4 | 10 | n |
| 5 | 9 | 7 | 5 | n / 2 |
| 8 | 9 | 8 | 2 | n / 4 |
| 9 | 9 | 9 | 1 | n / 8 |
您注意到#元素列中的序列有什么变化吗?
我们将其除以二,或多或少,直到达到零。
您注意到第n列的序列有什么变化吗?
2
4
8
二的幂!
通过在每次迭代中除以我们的输入,我们就可以对指数进行求逆。
📝 当您看到这种模式时,其中输入在每次迭代中被划分,它是 O(log n)。
大 O 对数时间复杂度
O(log n) 可以扩展吗?
确实。
在本教程中,你通过 JavaScript 示例学习了 Big O 对数时间复杂度的基础知识。敬请关注 Big O 符号系列的第五部分,我们将探讨 O(n log n),即对数线性时间复杂度。如果你想随时了解最新资讯,请订阅我的每周简报“解决方案”。
文章来源:https://dev.to/nielsenjared/big-o-logarithmic-time-complexity-gng 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com