算法的简单方法（第一部分）

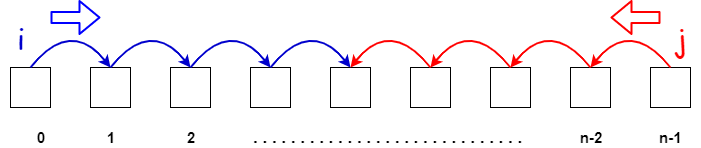
双指针技术

顶级公司通常会根据您展现出的解决问题的能力来聘用您。经验较少的工程师会被选中，而不是经验丰富的工程师。什么技能使一个人脱颖而出？您解决问题的能力有多强，而不是您解决了多少问题。算法是像谷歌这样的大型科技公司用来测试解决问题能力的指标。通过学习双指针技术（算法基础系列中的第一部分），您可以展示您世界一流的能力。我们讨论使用具有最佳性能的大 O 符号的优化算法来节省时间和空间。
双指针技术涉及在排序数组中使用两个数组索引。目的是节省时间和空间。通常放置在数组的两端，它可以在优化的时间内找到配对。一个典型的问题是这样的：

示例：在一个未排序的数组中，查找是否存在给定和 targetSum 的对。
一种典型的暴力破解方法是创建一个函数，并在其中嵌套一个 for 循环来比较对：

pairExists(array, targetSum) { 
for(let i = 0; i < array.length -1; i++){
        let firstNumber = array[i];

        for(let j = i + 1; j < array.length; j++){
            let secondNumber = array[j];

            if(firstNumber + secondNumber === targetSum){
                return [firstNumber, secondNumber];
            }
        }
    }
}

上述嵌套 for 循环方法会导致O(n^2) 的时间复杂度，因为我们在算法中迭代了两次。虽然这可能有效，但当我们将数组的大小增加到一百万时，它就不再是最佳方案了。

双指针技术示例

两个数字之和：

编写一个函数，输入一个无序的不同整数数组和一个表示目标和的整数。如果任意两个数之和等于目标和，则返回一个数组。如果没有两个数之和等于目标和，则返回一个空数组。

要点：

• 未排序数组
• 不同的整数
• 目标总和

// o(nlog(n)) | o(1) space
function twoNumberSum(array, targetSum) {
    array.sort((a, b) => a - b);
    let left = 0;
    let right = array.length - 1;

    while(array[left] < array[right]){
        const currentValue = array[left] + array[right];
        if (currentValue === targetSum ){
            return [array[left], array[right]]
        }
        else if (currentValue < targetSum){
            left++;
        }
        else if (currentValue > targetSum){
            right--;
        }
    }
    return [];
}

首先，我们在O(N*log(N))中对数组进行排序，这比蛮力方法中的 O(n^2) 好得多。有关更多信息，请参阅本文
。 然后我们设置指针变量并将它们称为left和right 。我们从索引 0 处的数组开头和array.length -1处的数组结尾进行迭代，如果我们得到的值小于目标总和，则将左指针向前移动，如果我们得到的值大于目标总和，则将右指针向前移动。
双指针算法通常只使用一个循环来迭代和比较值！与嵌套循环的蛮力方法相比，这是相当优化的。while
循环在O(n)时间和O(1) 空间复杂度内迭代（它不会创建另一个数组来检查值）。

复杂性
最后，我们可以说我们的两个数字和算法在O（N*log（N））时间和 O（1）空间算法中运行，因为数组排序函数是我们算法执行的最高时间复杂度。

三数之和：

编写一个函数，输入一个未排序的不同整数数组和一个表示目标和的整数。该函数应在数组中找出三个和等于目标和的数字。返回一个按升序排列的二维数组。如果找不到三个等于目标和的数字，则返回一个空数组。

要点：

• 未排序数组
• 不同的整数
• 目标总和
• 返回按升序排序的二维数组
• 返回空数，总和不等于目标和

// o(n^2) time | o(n) space
function threeNumberSum(array, targetSum) {
    array.sort((a,b) => a - b);
    let tripleValueArray = [];
    for (let i = 0; i < array.length - 2; i++) {
        let leftNumber = i + 1;
        let rightNumber = array.length - 1;

        while (leftNumber < rightNumber) {
            let currentNumber = array[i] + array[leftNumber] +       array[rightNumber];

            if (currentNumber === targetSum) {
                tripleValueArray.push([ array[i], array[leftNumber], array[rightNumber] ]);
                leftNumber++;
                rightNumber--;
            } else if (currentNumber < targetSum) {
                leftNumber++;
            } else if (currentNumber > targetSum) {
                rightNumber--;
            }
        }
    }
    return tripleValueArray;
}

首先，我们在O(N*log(N))中对数组进行排序，这比使用三个 for 循环嵌套的强力方法 O(n^3) 要好得多。
接下来，我们在循环中使用for (let i=0; i < array.length - 2; i++)，因为我们总是想要两个额外的值来检查而不是迭代。记住，三数之和的指针位置如下所示：
[ -8, -6 , 1, 2, 3, 5, 6, 12 ]
其中-8是当前的起始数字，-6是左边的起始数字，12 是右边的起始数字。如果三个值的总和小于目标和，我们就移动左指针，如果三个值的总和大于目标和，我们就移动右指针。

记住，数组是排序的，因此从左到右或从右到左移动会分别增加或减少总和值。-8+(-6)+12 的总和 = -2。但是，如果我们将左指针从-6 移动到 1，总和-8+1+12 = 5。这是一个更大的数字！同样，将右指针从-12移动到 -8 ，结果将是-8+(-6)+6 = -8。这是一个小得多的数字。

当我们将两个指针移向中间时，唯一的条件是如果 (currentNumber === targetSum) ，则三个值的总和等于目标总和。我们使用条件：
leftNumber++;和rightNumber--;来跳出 while 循环。然后，我们返回推送到tripleValueArray中的任何内容。如果没有推送任何内容，我们将返回它，因为它被声明为一个空数组。

复杂度：由于算法中包含两个循环，即外层 for 循环和内层 while 循环，因此三数和的时间复杂度为
O ( N^2)
。由于创建时间是常数，因此 空间复杂度为O(N)。不过，我们无法确定三值数组 (tripleValueArray) 的大小。

四数和

编写一个函数，输入一个未排序的不同整数数组和一个表示目标和的整数。该函数应在数组中找出四个和等于目标和的数字。返回一个无特定顺序的二维数组。如果找不到四个等于目标和的数字，则返回一个空数组。

// o(n^2) time | o(n^2) space
function fourNumberSum(array, targetSum) {
    const temporaryPairSum = {};
    const quadruplet = [];

    for (let i=1; i < array.length - 1; i++){
        for(let j = i+1; j < array.length; j++){
            let currentSum = array[i] + array[j];
            let difference = targetSum - currentSum;

            if ( difference in temporaryPairSum){
                for (const arrayPair of temporaryPairSum[difference]){
                    quadruplet.push(arrayPair.concat([array[i], array[j]]))
                }
            }
        }
        for (let k=0; k < i; k++){
            let currentSum = array[k] + array[i];
            if(!(currentSum in temporaryPairSum)){
                temporaryPairSum[currentSum] = [[array[k], array[i]]];
            } else {
                temporaryPairSum[currentSum].push([array[k], array[i]]);
            }
        }
    }
    return quadruplet;

}

我们使用哈希表来存储对的值。对于此算法，我们从索引 1开始外层 for 循环，并迭代到array.length - 1索引。等式的内层 for 循环也从索引 1 + 1 位置开始。但是我们为什么要这样做呢？

我们希望避免值重复，因此在第一次迭代期间，我们跳过在哈希表temporaryPairSum中保存任何内容。我们仅在从索引 0开始第二次迭代时保存值，同时将这些值与数组索引“i”中的当前值进行比较，如公式(let k=0; k < i; k++)的这一部分所示。

记住，我们通过从数组索引 1开始for (let i=1; i < array.length - 1; i++)来跳过外部 for 循环中的第一个值。

接下来，我们求解多维数组中的另外两个数组，并将其从目标和中减去。然后检查哈希表中是否存在差值

const difference = targetSum - currentSum;
 if ( difference in temporaryPairSum)

如果确实如此，那么恭喜你！我们将这两个数组值推送到我们的四元组多维数组中。

内层 for 循环的第二部分就是我们之前提到的“差异”被添加的地方。一定要仔细观察！

我们从索引 0开始迭代，直到外层 for 循环的迭代当前所在的位置 (let k =0; k < i; k++)。然后，我们检查是否已初始化两个数组对的和（在外层 for 循环中称为 diff）。如果没有初始化，我们在这里进行初始化：
allPairSum[currentSum] = [[array[k], array[i]]];

请注意，我们的哈希表使用两个数组对之和作为键，并使用一个多维数组作为值。这有助于追踪迭代过程中可能出现的重复项。例如，假设目标和差为 17，则包含重复项的哈希表如下所示：

{
17: "[ [array[k], array[i]], [array[k], array[i]]  ]"
}

重复项是相同值的不同排列。

 7 + 10 = 17 and 10 + 7 = 17:
{
17: "[ [10, 7], [7, 10]  ]"
}

我们使用此行allPairSum[currentSum].push([array[k], array[i]]);将重复项推送到哈希表；

算法结束时返回四元组多维数组。如果未找到四元组，则返回空数组。

复杂度：该算法的
平均时间复杂度分析为O(2N^2)，最终结果为 O(N^2)。这是因为在大 O 扩展中，常数N（此处为 2）是无关紧要的。主要的复杂度来自于 N 的未知大小。该算法的最坏情况为O(N^3)。

您可能还想知道为什么在大约 4 个 for 循环之后我们的时间复杂度只有O(N^2) ？这是因为其中 2 个内层 for 循环开始于外层 for 循环的起始索引之前或之后。如果仔细观察，第一个内层 for 循环从外层 for 循环for(let j = i+1; j < array.length; j++)旁边的索引开始，而等式for (let k=0; k < i; k++)的最后一个 for 循环在外层 for 循环之前开始。这些类型的 for 循环计算结果为O(2N)。我们通过添加外层 for 循环的时间复杂度得到O(2N^2) = O(N^2)。对于最坏情况O(N^3) ，它是用于迭代哈希表中for (const arrayPair of temporaryPairSum[difference])中的对重复项的时间复杂度。

空间复杂度为 O(n^2)，因为您永远不知道哈希表或四元组多维数组可能占用的空间。

要了解 Big-O 符号，请参阅本文。如需进一步了解，请访问此链接。