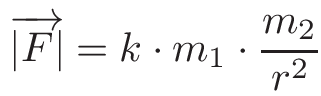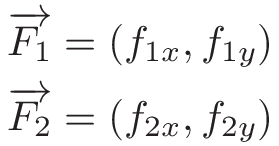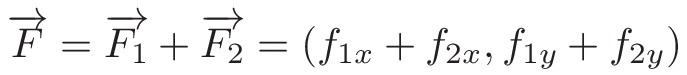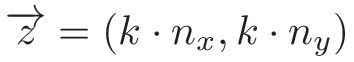在 JavaScript 中实现 2D 物理
注:本文最初发布于martinheinz.dev
物理原理和逼真动画的实现看似复杂难懂,但事实并非如此。这些算法可以非常简单,并且可以对各种物理概念(包括速度、加速度或重力)进行逼真的模拟。
那么,让我们看看这些算法在使用 JavaScript 实现 2D 物理模拟时是如何工作的!
您可以在此处查看动画和示例:https://martinheinz.github.io/physics-visual/
TL;DR:源代码可在我的存储库中找到:https://github.com/MartinHeinz/physics-visual
匀速加速运动
让我们从最基本的事情开始——移动东西。
如果我们只想要均匀运动,那么我们可以使用如下代码:
function move(dt) {
x += vx * dt;
y += vy * dt;
}
在上面的代码中x,和y是对象(例如椭圆)的坐标,接下来vx和vy分别是水平和垂直轴上的速度,并且dt(时间增量)是两次计时器滴答之间的时间,在JavaScript的情况下是两次调用requestAnimationFrame。
举个例子 - 如果我们想要移动位于(150, 50)西南方向的物体,那么我们会有以下内容(单次滴答后移动):
x = 150 += -1 * 0.1 -> 149.9
y = 50 += 1 * 0.1 -> 50.1
然而,均匀移动非常无聊,所以让我们加速物体的移动:
function move(dt) {
vx += ax * dt;
vy += ay * dt;
x += vx * dt;
y += vy * dt;
}
在这段代码中,我们添加了ax和,分别ay表示x轴和y轴上的加速度。我们利用加速度计算速度或速率的变化( ),然后像之前一样用它来移动物体。现在,如果我们复制前面的例子,只在x轴(向西)vx/vy上添加加速度,我们得到:
vx = -1 += -1 * 0.1 -> -1.1 // vx += ax * dt;
vy = 1 += 0 * 0.1 -> 1 // vy += ay * dt;
x = 150 += -1.1 * 0.1 -> 149.89 // x += vx * dt; Moved further (-0.01) than in previous example!
y = 50 += 1 * 0.1 -> 50.1 // y += vy * dt;
重力
既然我们已经可以移动物体了,那么如何让物体向其他物体移动呢?嗯,这就是所谓的重力。为了实现它,我们需要添加什么呢?
为了让你知道我们想要达到什么目的:
首先,让我们回顾一下高中时的一些等式:
力的方程:
F = m * a ... Force is Mass times Acceleration
a = F / m ... From that we can derive that force acting on some object (mass) accelerates
如果我们现在想将其扩展到两个物体相互作用的力,我们会得到:
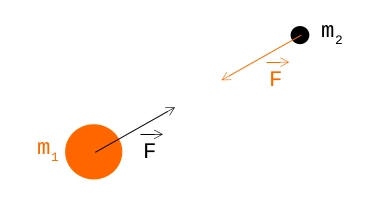
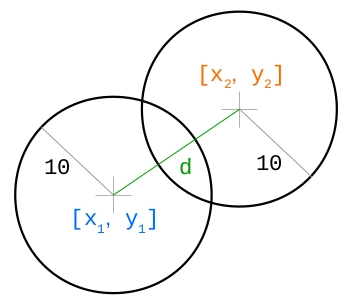
这有点复杂(至少对我来说是这样),所以我们来分解一下。在这个方程中|F|,力的大小对两个物体来说是一样的,只是方向相反。这些物体用它们的质量来表示——m_1还有m_2……k这是引力常数,r是这些物体重心之间的距离。如果还是不明白,可以看一张图片:
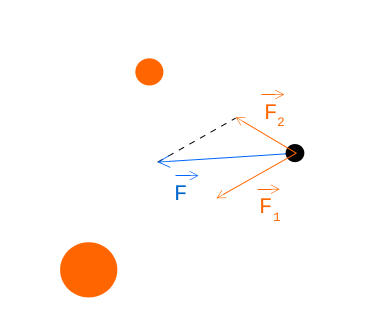
如果我们想要创建一些可视化效果,最终会得到两个以上的对象,对吧?那么,当有更多对象相互作用时会发生什么呢?
看上图,我们可以看到两个橙色物体以和的力拉着黑色物体,F_1但F_2我们感兴趣的是最终的力F,我们可以这样计算:
- 我们首先计算力
F_1,并F_2利用上面的方程 - 然后我们将其分解为向量:
- 最后我们得到
F:
好了,我们需要的数学知识都搞定了,现在代码会是什么样子呢?我会省略所有步骤,只展示最终代码并附上注释。如果您需要更多信息,请随时联系我。🙂
function moveWithGravity(dt, o) { // "o" refers to Array of objects we are moving
for (let o1 of o) { // Zero-out accumulator of forces for each object
o1.fx = 0;
o1.fy = 0;
}
for (let [i, o1] of o.entries()) { // For each pair of objects...
for (let [j, o2] of o.entries()) {
if (i < j) { // To not do same pair twice
let dx = o2.x - o1.x; // Compute distance between centers of objects
let dy = o2.y - o1.y;
let r = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2));
if (r < 1) { // To avoid division by 0
r = 1;
}
// Compute force for this pair; k = 1000
let f = (1000 * o1.m * o2.m) / Math.pow(r, 2);
let fx = f * dx / r; // Break it down into components
let fy = f * dy / r;
o1.fx += fx; // Accumulate for first object
o1.fy += fy;
o2.fx -= fx; // And for second object in opposite direction
o2.fy -= fy;
}
}
}
for (let o1 of o) { // for each object update...
let ax = o1.fx / o1.m; // ...acceleration
let ay = o1.fy / o1.m;
o1.vx += ax * dt; // ...speed
o1.vy += ay * dt;
o1.x += o1.vx * dt; // ...position
o1.y += o1.vy * dt;
}
}
碰撞
当物体移动时,它们在某个时刻也会发生碰撞。我们有两种解决碰撞的方案——将物体推离碰撞或弹开。我们先来看看推离碰撞的解决方案:
在解决碰撞之前,我们需要首先检查两个物体是否确实发生碰撞:
class Collision {
constructor(o1, o2, dx, dy, d) {
this.o1 = o1;
this.o2 = o2;
this.dx = dx;
this.dy = dy;
this.d = d;
}
}
function checkCollision(o1, o2) {
let dx = o2.x - o1.x;
let dy = o2.y - o1.y;
let d = Math.sqrt(Math.pow(dx, 2) + Math.pow(dy, 2));
if (d < o1.r + o2.r) {
return {
collisionInfo: new Collision(o1, o2, dx, dy, d),
collided: true
}
}
return {
collisionInfo: null,
collided: false
}
}
我们首先声明Collision一个表示两个碰撞物体的类。在checkCollision函数中,我们首先计算物体距离的x和分量,然后计算它们的实际距离。如果它们的半径和小于它们的距离,则它们一定发生了碰撞,因此我们返回一个新物体。yddCollision
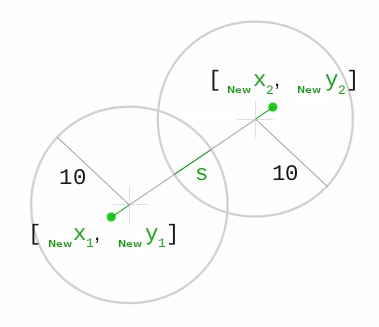
现在,为了解决它们的碰撞,我们需要知道位移的方向及其大小:
n_x = d_x / d ... this is eigenvector
n_y = d_y / d
s = r_1 + r_2 - d ... s is size of collision (see picture)
因此,在 JavaScript 代码中将是:
function resolveCollision(info) { // "info" is a Collision object from above
let nx = info.dx /info.d; // Compute eigen vectors
let ny = info.dy /info.d;
let s = info.o1.r + info.o2.r - info.d; // Compute penetration depth
info.o1.x -= nx * s/2; // Move first object by half of collision size
info.o1.y -= ny * s/2;
info.o2.x += nx * s/2; // Move other object by half of collision size in opposite direction
info.o2.y += ny * s/2;
}
您可以在https://martinheinz.github.io/physics-visual/查看此碰撞解决方案的交互式示例(单击“推动物体”)
用力解决碰撞
还有最后一块拼图——通过物体弹跳来解决碰撞。在这种情况下,最好省略所有数学知识,因为这会使文章篇幅增加一倍。所以我只想告诉你,我们需要考虑动量守恒定律和能量守恒定律,这有助于我们构建和求解以下神奇方程:
k = -2 * ((o2.vx - o1.vx) * nx + (o2.vy - o1.vy) * ny) / (1/o1.m + 1/o2.m) ... *Magic*
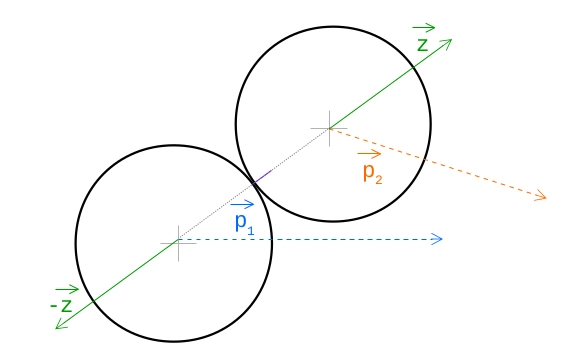
那么,这个魔法k对我们有什么帮助呢?我们知道物体移动的方向(我们可以像之前那样,用特征向量n_x计算方向)n_y,但我们不知道移动的幅度,这就是k。因此,我们这样计算向量 ( z),它告诉我们应该把物体移动到哪里:
现在是最终代码:
function resolveCollisionWithBounce(info) {
let nx = info.dx /info.d;
let ny = info.dy /info.d;
let s = info.o1.r + info.o2.r - info.d;
info.o1.x -= nx * s/2;
info.o1.y -= ny * s/2;
info.o2.x += nx * s/2;
info.o2.y += ny * s/2;
// Magic...
let k = -2 * ((info.o2.vx - info.o1.vx) * nx + (info.o2.vy - info.o1.vy) * ny) / (1/info.o1.m + 1/info.o2.m);
info.o1.vx -= k * nx / info.o1.m; // Same as before, just added "k" and switched to "m" instead of "s/2"
info.o1.vy -= k * ny / info.o1.m;
info.o2.vx += k * nx / info.o2.m;
info.o2.vy += k * ny / info.o2.m;
}
结论
这篇文章包含大量数学知识,但大部分都很简单,希望能够帮助你理解并熟悉这些物理概念。如果你想了解更多细节,可以查看我代码库中的代码(此处),以及交互式演示(此处)。
鏂囩珷鏉ユ簮锛�https://dev.to/martinheinz/implementing-2d-physicals-in-javascript-1c99 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com