数据结构和算法：0 到 60

无论是家庭作业还是面试，数据结构和算法都将是你早期职业生涯的基础。本文旨在帮助你从零开始，掌握计算机科学这一关键领域的实用知识。

链表

顾名思义，链表就是一个包含多个元素的列表。每个元素都指向列表中的下一个节点。可以把链表想象成寻宝游戏。

你从一条线索（链表的头部）开始，每条线索都会引导你找到下一条线索（下一个指针），直到链表的末尾（链表的尾部）。你能想到一个链表的实现吗？

使用链表的一些常见原因包括：

• 在数据中间插入元素：只要您知道插入索引之前的节点，就可以在列表的任何位置插入元素。向量中为 O(n)，链表中为 O(1)。
• 更快地扩展数据空间：由于链表专注于使用指针的理念，因此您无需为数据分配连续的内存块。与简单的 Vector 实现相比，这可以节省 O(n) 的时间复杂度。

链表的一个主要缺点是无法通过索引随机访问列表中的元素。例如：如果你想检索列表中的第 5 个元素，就必须遍历整个列表，直到找到它为止。

堆栈/队列

栈和队列本质上是相同的数据结构，唯一的区别在于它们对信息的排序方式。我们可以使用之前的 Node 结构体来实现这两个结构！

堆栈遵循后进先出 (LIFO) 原则。想象一下一堆自助餐托盘。最后一个放入的托盘将是你第一个从中取出的托盘。堆栈有三个主要功能：一个是查看堆栈顶部，一个是将托盘推到堆栈顶部，一个是将托盘从堆栈顶部弹出。

队列遵循先进先出的原则。想象一下排队等候的队列。如果你排在第一位，你会最先得到帮助。同样，如果你排在最后，你会最后得到帮助。队列提供的功能与堆栈相同，只是推送的实现略有不同。（我们希望推送到队列末尾。）

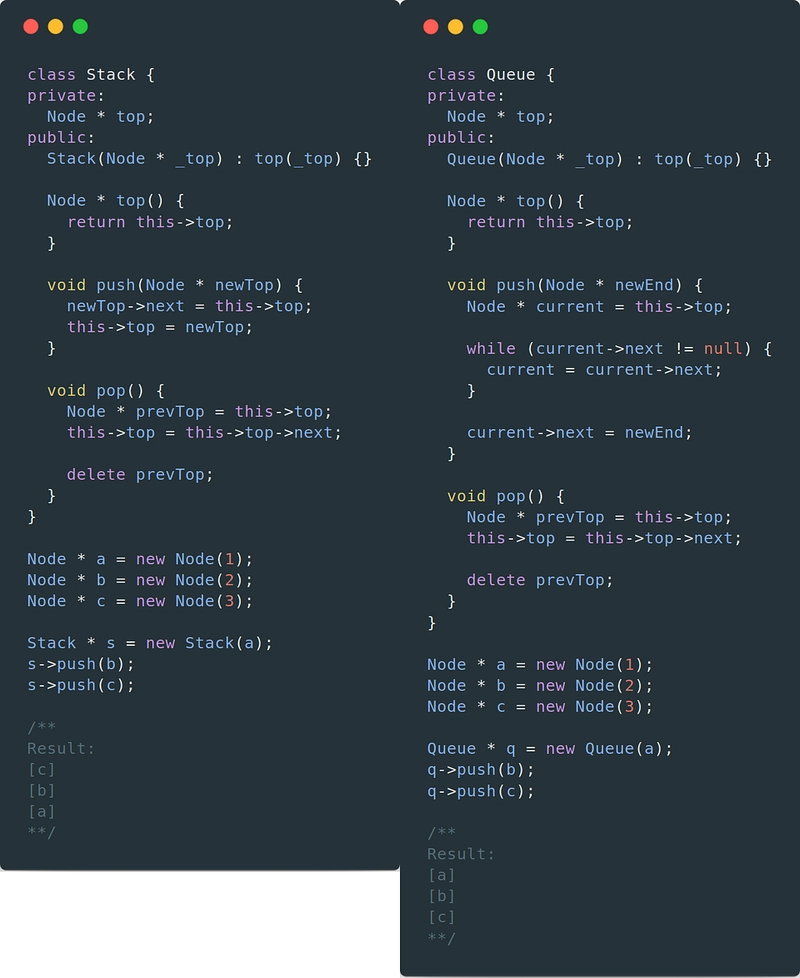
堆栈和队列非常适合根据插入时间维护顺序：如果您想跟踪最新的项目，请使用堆栈。如果您想跟踪最旧的项目，请使用队列。

如果您关心的不是最新或最旧的项目，请不要使用任何一个。

树木

树是一种非常适合数据中父子关系的数据结构。它可以用我们上面定义的简单 Node 类来实现，只不过它有多个 children 指针，而不是一个 next 指针。

树需要的思维方式与向量、链表，甚至栈/队列都不同。它们引入了遍历树的概念。由于没有固定的从父节点到子节点的路径，因此你可以选择三种主要的遍历方法：

前序遍历

如果您想在对子级进行相同计算之前先对父级进行计算，请使用预序遍历。

给出上面的树形表示：

中序遍历

如果要计算左子节点、父节点，最后是右子节点的某个值，请使用中序遍历。这通常只用于二叉树，即每个节点最多只有两个子节点的树。

给出上面的树形表示：

后序遍历

如果您想在对父级进行某些计算之前先对子级进行某些计算，请使用后序遍历。

给出上面的树形表示：

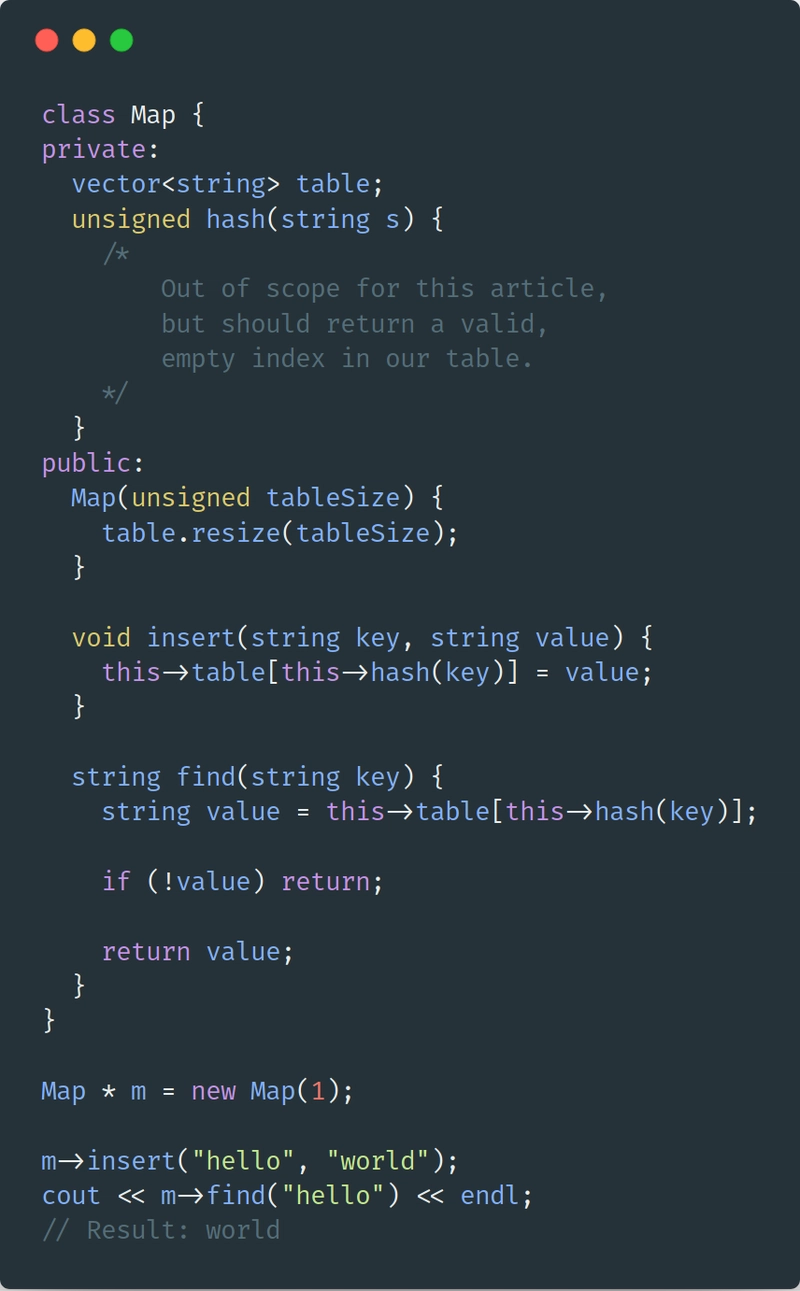
地图

Map是一种用键和值来表示数据的方式。正确的实现可以实现非常快速的插入、查找和删除操作。

好的 Map 实现的基础是它的哈希函数。哈希函数的作用是：

• 给定任何有效输入，提供散列或编码的输出
• 对于相同的输入，始终返回相同的输出
• 当两个输入返回相同的输出时，最小化碰撞

地图非常强大，因为你可以快速地操作它们。（插入、删除和查找的时间复杂度为 O(1)！）这种速度非常适合大多数面试问题，甚至可以让它们变得微不足道。

充分了解地图。

图表

图是一种灵活的数据结构，可用于表示节点之间具有复杂关系的数据。它与链表非常相似，但每个节点可以包含 n 个指向其他节点的指针。图也不能保证没有环路。（环路是指在遍历图中，起点和终点可能都在同一节点。）

Graph 的实现实际上非常简单：

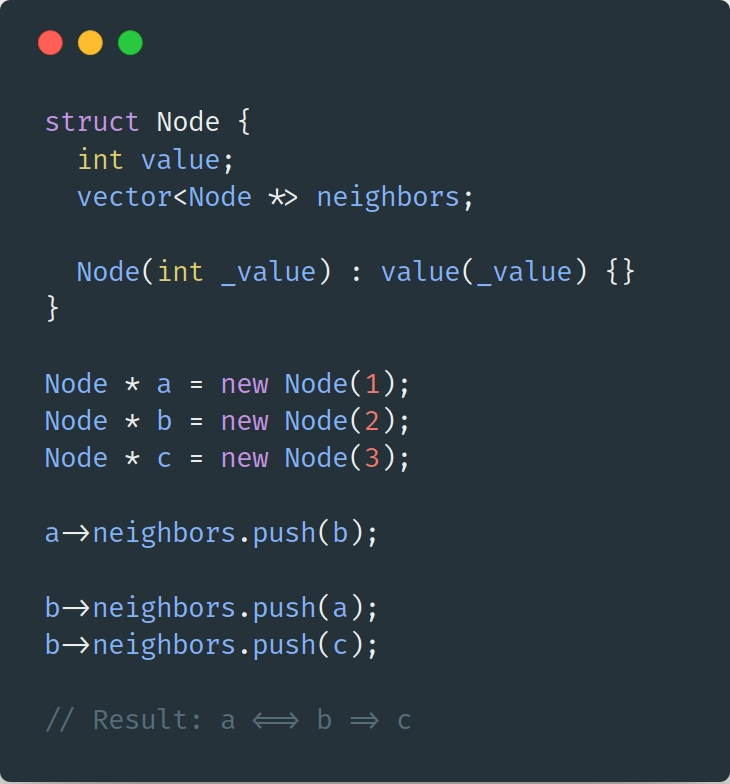
我们可以用图来模拟很多情况，例如：用户之间的友谊关系、飞行路线等等。图可以使任何具有复杂关系的问题变得非常简单，从一个节点到另一个节点就像遍历其邻居一样简单。（示例见附录：路径查找和 Dijkstra 算法。）

附录

这些是一些可以在课程大纲和面试题中找到的基本数据结构。如果你想进一步扩展你的知识（从 60 到 120！），这里有一些高级数据结构和算法：

• 链表中的循环
• 使用 Stack 来计算数学表达式
• Tries：一种允许高效路径查找的奇特树
• 集合：当您只想记住某个元素是否曾经见过时（map<[anything], bool> 的绝佳替代品）
• 路径查找算法（Kruskal 算法和Prim 算法），用于查找图中两个节点之间的路径
• Dijkstra 算法：找到两个节点之间阻力最小的路径

更多资源

如果您更喜欢书籍而不是博客文章，我强烈推荐（按可读性顺序）：

• 算法人生：人类决策的计算机科学：一本关于如何在日常生活中应用算法的好书。学术性不强。
• Grokking Algorithms：这是一本令人难以置信的书，不仅因为它简单的解释和与现实世界例子的联系，还因为它有图片！
• 算法导论，第 3 版：一本很棒的参考书，用于 UCR 的中级数据结构和算法。
• 《算法》第四版：由传奇人物 Robert Sedgewick 撰写，内容极其丰富。（Sedgewick 自 Fortran 鼎盛时期就开始教授算法了！）