不到 500 行代码即可实现自动泊车
使用遗传算法训练汽车自动停车
TL;DR
在本文中,我们将使用遗传算法训练汽车进行自动停车。
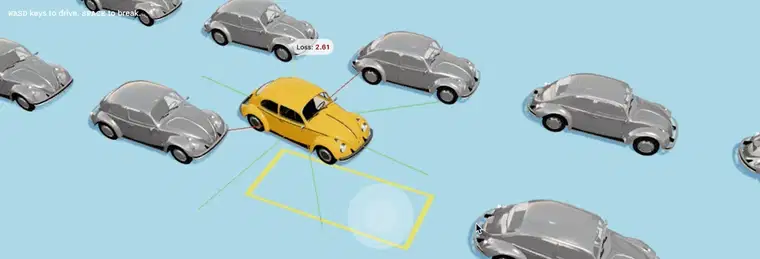
我们将创造第一代具有随机基因组的汽车,其行为方式如下:
到了第 40 代,汽车开始学习自动停车,并开始靠近停车位:
另一个起点更具挑战性的例子:
是啊,这些车一路上撞到了其他车,而且停车位也不完美,但这只是它们诞生以来的第 40 代,所以请仁慈一些,给这些车一些成长空间 :D
您可以启动🚕自动泊车进化模拟器,直接在浏览器中查看进化过程。该模拟器为您提供以下功能:
- 您可以从头开始训练汽车并自行调整遗传参数
- 你可能会看到经过训练的自动泊车正在运行
- 您也可以尝试手动停车
本项目的遗传算法是用 TypeScript 实现的。完整的遗传算法源代码将在本文中展示,您也可以在Evolution Simulator 代码库中找到最终的代码示例。
我们将使用遗传算法来完成汽车基因组进化这一特定任务。然而,本文仅涉及该算法的基础知识,并非遗传算法主题的完整指南。
话虽如此,让我们深入了解更多细节......
计划
我们将逐步把创建自动泊车的高级任务分解为寻找最佳180位组合(寻找最佳汽车基因组)的直接低级优化问题。
以下是我们要做的事情:
- 💪🏻 为汽车提供动力(发动机、方向盘),使其能够驶向停车位。
- 👀 给汽车装上眼睛(传感器),让它能够看到周围的障碍物。
- 🧠 给汽车装上“大脑”,让它根据所见(通过传感器识别的障碍物)来控制肌肉(运动)。“大脑”本身只是一个纯粹的功能
movements = f(sensors)。 - 🧬进化大脑,使其根据传感器输入做出正确的动作。我们将在这里应用遗传算法。一代又一代,我们的大脑功能
movements = f(sensors)将学习如何将汽车驶向停车位。
为汽车提供动力
为了能够移动,汽车需要“肌肉”。我们来为汽车添加两种肌肉:
- 发动机动力——使汽车可以向后移动 ↓、向前移动 ↑或静止不动(空档)
- 方向盘肌肉- 允许汽车在行驶过程中向左←、向右→或直行
利用这两块肌肉,汽车可以完成以下动作:
在我们的例子中,肌肉接收来自大脑每(毫秒)一次的信号100ms。根据大脑信号的大小,肌肉会做出不同的反应。我们将在下文中讨论“大脑”部分,但现在我们假设大脑可能只向每块肌肉发送 3 种可能的信号:-1、0或+1。
type MuscleSignal = -1 | 0 | 1;
+1例如,大脑可能会向发动机肌肉发送值为 的信号,汽车就会开始向前行驶。-1向发动机发送的信号会使汽车向后行驶。同时,如果大脑-1向方向盘肌肉发送 的信号,汽车就会向左转,等等。
在我们的案例中,脑信号值与肌肉动作的映射如下:
| 肌肉 | Signal = -1 |
Signal = 0 |
Signal = +1 |
|---|---|---|---|
| 引擎 | ↓ 后退 | ◎ 中性 | ↑ 前进 |
| 方向盘 | ← 左 | ◎ 直 | → 右 |
你可以使用 Evolution 模拟器尝试手动停车,看看汽车肌肉是如何工作的。每次按下
WASD键盘上的某个键(或使用触摸屏操纵杆)时,你都会向发动机和方向盘肌肉发送这些-1、0、 或信号。+1
给汽车添点睛之笔
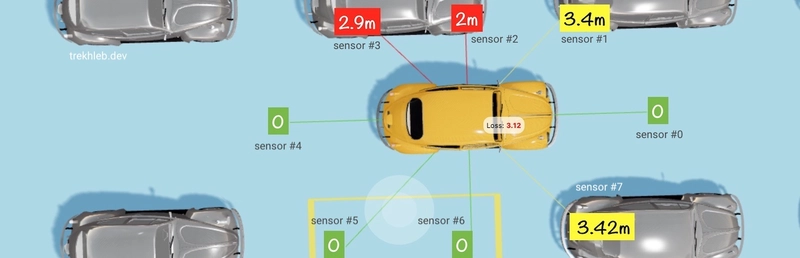
在我们的汽车学会如何利用肌肉进行自动泊车之前,它需要能够“看到”周围的环境。让我们8用距离传感器给它装上“眼睛”:
- 每个传感器可以检测到距离范围内的障碍物
0-4m(米)。 - 每个传感器每天都会向汽车的“大脑”报告它“看到”的障碍物的最新信息
100ms。 - 每当传感器没有检测到任何障碍物时,它就会报告 的值
0。相反,如果传感器的值很小但不为零(即0.01m),则表示障碍物很近。
您可以使用 Evolution Simulator并观察每个传感器的颜色如何根据障碍物的接近程度而变化。
type Sensors = number[];
为汽车注入“大脑”
目前,我们的汽车可以“看”和“动”,但还没有一个“协调器”,把“眼睛”的信号转化为“肌肉”的正确动作。我们需要给汽车一个“大脑”。
大脑输入
作为来自传感器的输入,100ms大脑将获得每个8浮点数,每个浮点数都在 的范围内[0...4]。例如,输入可能如下所示:
const sensors: Sensors = [s0, s1, s2, s3, s4, s5, s6, s7];
// i.e. 🧠 ← [0, 0.5, 4, 0.002, 0, 3.76, 0, 1.245]
大脑输出
每个100ms大脑都应该产生两个整数作为输出:
- 一个数字作为引擎的信号:
engineSignal - 一个数字作为方向盘的信号:
wheelSignal
每个数字应属于类型MuscleSignal,并可采用以下三个值之一:-1、0或+1。
大脑公式/功能
记住上面提到的大脑的输入和输出,我们可以说大脑只是一种功能:
const { engineSignal, wheelSignal } = brainToMuscleSignal(
brainFunction(sensors)
);
// i.e. { engineSignal: 0, wheelSignal: -1 } ← 🧠 ← [0, 0.5, 4, 0.002, 0, 3.76, 0, 1.245]
其中brainToMuscleSignal()是一个函数,它将原始脑信号(任意浮点数)转换为肌肉信号(转换为-1、0或+1数字),以便肌肉能够理解。我们将在下面实现这个转换函数。
现在的主要问题是这brainFunction()是一个什么样的功能。
为了让汽车更智能、动作更精准,我们可以采用多层感知器。名字听起来有点吓人,但这是一个具有基本架构的简单神经网络(可以把它想象成一个包含许多参数/系数的大公式)。
我在自制机器学习、机器学习实验和纳米神经元项目中更详细地介绍了多层感知器。你甚至可以挑战一下这个简单的网络来识别你手写的数字。
然而,为了避免引入全新的神经网络概念,我们将采用一种更简单的方法,使用两个具有多个变量的线性多项式(更准确地说,每个多项式都有确切的8变量,因为我们有8传感器),它看起来像这样:
engineSignal = brainToMuscleSignal(
(e0 * s0) + (e1 * s1) + ... + (e7 * s7) + e8 // <- brainFunction
)
wheelSignal = brainToMuscleSignal(
(w0 * s0) + (w1 * s1) + ... + (w7 * s7) + w8 // <- brainFunction
)
在哪里:
[s0, s1, ..., s7]-8变量,即8传感器值。这些是动态的。[e0, e1, ..., e8]-9引擎多项式的系数。汽车需要学习这些系数,并且这些系数是静态的。[w0, w1, ..., w8]-9方向盘多项式的系数。汽车需要学习这些系数,它们是静态的
使用更简单的大脑功能的代价是,汽车将无法学习一些复杂的动作,也无法很好地泛化和适应未知环境。但对于我们特定的停车场,以及为了演示遗传算法的工作原理,这仍然足够了。
我们可以用以下方式实现通用多项式函数:
type Coefficients = number[];
// Calculates the value of a linear polynomial based on the coefficients and variables.
const linearPolynomial = (coefficients: Coefficients, variables: number[]): number => {
if (coefficients.length !== (variables.length + 1)) {
throw new Error('Incompatible number of polynomial coefficients and variables');
}
let result = 0;
coefficients.forEach((coefficient: number, coefficientIndex: number) => {
if (coefficientIndex < variables.length) {
result += coefficient * variables[coefficientIndex];
} else {
// The last coefficient needs to be added up without multiplication.
result += coefficient
}
});
return result;
};
在这种情况下,汽车的大脑将由两个多项式组成,如下所示:
const engineSignal: MuscleSignal = brainToMuscleSignal(
linearPolynomial(engineCoefficients, sensors)
);
const wheelSignal: MuscleSignal = brainToMuscleSignal(
linearPolynomial(wheelCoefficients, sensors)
);
函数的输出linearPolynomial()是一个浮点数。该brainToMuscleSignal()函数需要将大范围的浮点数转换为三个特定的整数,具体操作分为两步:
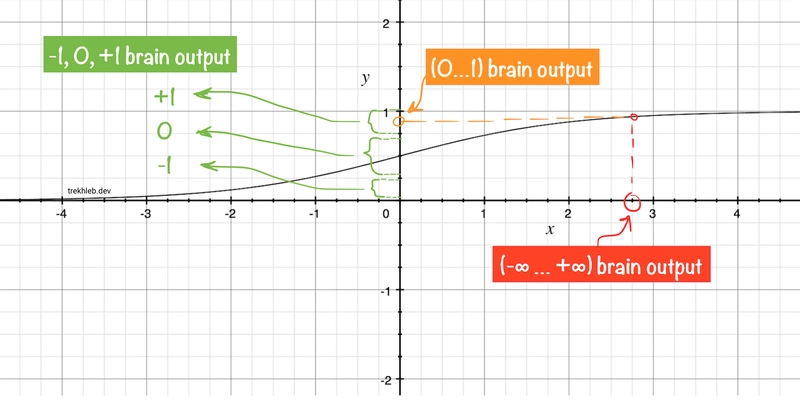
- 将宽范围的浮点数(即
0.456或3673.45或-280)转换为 范围内的浮点数(0...1)(即0.05或0.86) - 将 范围内的浮点数转换为、或
(0...1)三个整数值之一。例如,接近 的浮点数将被转换为,接近 的浮点数将被转换为,接近 的浮点数将被转换为。-10+10-10.5011
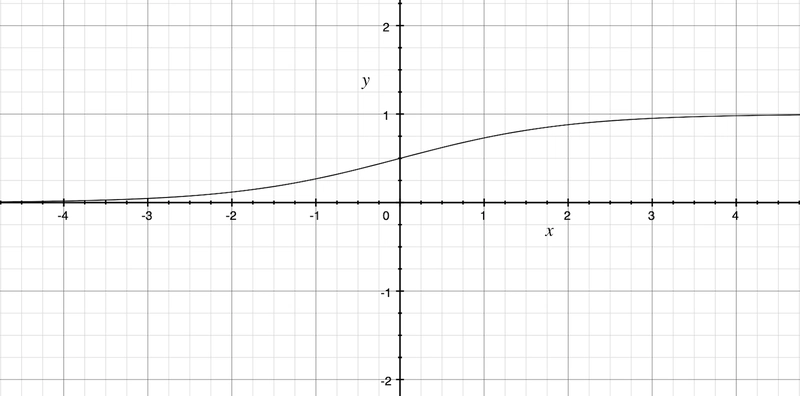
为了完成转换的第一部分,我们需要引入一个Sigmoid 函数,它实现以下公式:
它将范围较宽的浮点数(x轴)转换为范围有限的浮点数(0...1)(y轴)。这正是我们所需要的。
转换步骤在 Sigmoid 图上的表现如下。
上面提到的两个转换步骤的实现如下:
// Calculates the sigmoid value for a given number.
const sigmoid = (x: number): number => {
return 1 / (1 + Math.E ** -x);
};
// Converts sigmoid value (0...1) to the muscle signals (-1, 0, +1)
// The margin parameter is a value between 0 and 0.5:
// [0 ... (0.5 - margin) ... 0.5 ... (0.5 + margin) ... 1]
const sigmoidToMuscleSignal = (sigmoidValue: number, margin: number = 0.4): MuscleSignal => {
if (sigmoidValue < (0.5 - margin)) {
return -1;
}
if (sigmoidValue > (0.5 + margin)) {
return 1;
}
return 0;
};
// Converts raw brain signal to the muscle signal.
const brainToMuscleSignal = (rawBrainSignal: number): MuscleSignal => {
const normalizedBrainSignal = sigmoid(rawBrainSignal);
return sigmoidToMuscleSignal(normalizedBrainSignal);
}
汽车基因组(DNA)
☝🏻 上面“眼睛”、“肌肉”和“大脑”部分的主要结论应该是:系数
[e0, e1, ..., e8]和[w0, w1, ..., w8]定义了汽车的行为。这些18数字共同构成了独一无二的汽车基因组(或汽车的DNA)。
十进制形式的汽车基因组
让我们将[e0, e1, ..., e8]和[w0, w1, ..., w8]大脑系数连接在一起,以十进制形式形成汽车基因组:
// Car genome as a list of decimal numbers (coefficients).
const carGenomeBase10 = [e0, e1, ..., e8, w0, w1, ..., w8];
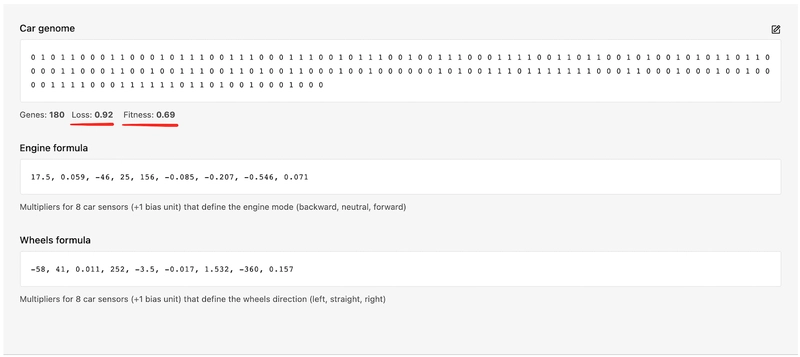
// i.e. carGenomeBase10 = [17.5, 0.059, -46, 25, 156, -0.085, -0.207, -0.546, 0.071, -58, 41, 0.011, 252, -3.5, -0.017, 1.532, -360, 0.157]
二进制形式的汽车基因组
让我们更深入一步(到基因层面),将汽车基因组的十进制数转换为二进制格式(转换为简单的1s 和0s)。
我在浮点数的二进制表示一文中详细描述了将浮点数转换为二进制数的过程。如果本节中的代码不太清晰,您可以查看一下。
下面是一个将浮点数转换为二进制数的简单示例(如果该示例令人困惑16 bits,请先阅读此内容):
在我们的例子中,为了减少基因组长度,我们将每个浮动系数转换为非标准10 bits二进制数(1符号位、4指数位、5分数位)。
18我们总共有个系数,每个系数都将转换为10位数。这意味着汽车的基因组将是一个由0和组成的数组1,长度为18 * 10 = 180 bits。
例如,对于上面提到的十进制格式的基因组,它的二进制表示形式如下:
type Gene = 0 | 1;
type Genome = Gene[];
const genome: Genome = [
// Engine coefficients.
0, 1, 0, 1, 1, 0, 0, 0, 1, 1, // <- 17.5
0, 0, 0, 1, 0, 1, 1, 1, 0, 0, // <- 0.059
1, 1, 1, 0, 0, 0, 1, 1, 1, 0, // <- -46
0, 1, 0, 1, 1, 1, 0, 0, 1, 0, // <- 25
0, 1, 1, 1, 0, 0, 0, 1, 1, 1, // <- 156
1, 0, 0, 1, 1, 0, 1, 1, 0, 0, // <- -0.085
1, 0, 1, 0, 0, 1, 0, 1, 0, 1, // <- -0.207
1, 0, 1, 1, 0, 0, 0, 0, 1, 1, // <- -0.546
0, 0, 0, 1, 1, 0, 0, 1, 0, 0, // <- 0.071
// Wheels coefficients.
1, 1, 1, 0, 0, 1, 1, 0, 1, 0, // <- -58
0, 1, 1, 0, 0, 0, 1, 0, 0, 1, // <- 41
0, 0, 0, 0, 0, 0, 1, 0, 1, 0, // <- 0.011
0, 1, 1, 1, 0, 1, 1, 1, 1, 1, // <- 252
1, 1, 0, 0, 0, 1, 1, 0, 0, 0, // <- -3.5
1, 0, 0, 0, 1, 0, 0, 1, 0, 0, // <- -0.017
0, 0, 1, 1, 1, 1, 0, 0, 0, 1, // <- 1.532
1, 1, 1, 1, 1, 0, 1, 1, 0, 1, // <- -360
0, 0, 1, 0, 0, 0, 1, 0, 0, 0, // <- 0.157
];
天哪!二进制基因组看起来太神秘了。但你能想象,180仅仅这些0和1就能定义汽车在停车场里的行为吗?这就像你黑进了某人的DNA,知道每个基因的确切含义一样。太神奇了!
顺便说一句,您可以在Evolution Simulator仪表板上看到性能最佳的汽车的基因组和系数的确切值:
以下是将浮点数从二进制转换为十进制格式的源代码(大脑需要它来解码基因组并根据基因组数据产生肌肉信号):
type Bit = 0 | 1;
type Bits = Bit[];
type PrecisionConfig = {
signBitsCount: number,
exponentBitsCount: number,
fractionBitsCount: number,
totalBitsCount: number,
};
type PrecisionConfigs = {
custom: PrecisionConfig,
};
const precisionConfigs: PrecisionConfigs = {
// Custom-made 10-bits precision for faster evolution progress.
custom: {
signBitsCount: 1,
exponentBitsCount: 4,
fractionBitsCount: 5,
totalBitsCount: 10,
},
};
// Converts the binary representation of the floating-point number to decimal float number.
function bitsToFloat(bits: Bits, precisionConfig: PrecisionConfig): number {
const { signBitsCount, exponentBitsCount } = precisionConfig;
// Figuring out the sign.
const sign = (-1) ** bits[0]; // -1^1 = -1, -1^0 = 1
// Calculating the exponent value.
const exponentBias = 2 ** (exponentBitsCount - 1) - 1;
const exponentBits = bits.slice(signBitsCount, signBitsCount + exponentBitsCount);
const exponentUnbiased = exponentBits.reduce(
(exponentSoFar: number, currentBit: Bit, bitIndex: number) => {
const bitPowerOfTwo = 2 ** (exponentBitsCount - bitIndex - 1);
return exponentSoFar + currentBit * bitPowerOfTwo;
},
0,
);
const exponent = exponentUnbiased - exponentBias;
// Calculating the fraction value.
const fractionBits = bits.slice(signBitsCount + exponentBitsCount);
const fraction = fractionBits.reduce(
(fractionSoFar: number, currentBit: Bit, bitIndex: number) => {
const bitPowerOfTwo = 2 ** -(bitIndex + 1);
return fractionSoFar + currentBit * bitPowerOfTwo;
},
0,
);
// Putting all parts together to calculate the final number.
return sign * (2 ** exponent) * (1 + fraction);
}
// Converts the 8-bit binary representation of the floating-point number to decimal float number.
function bitsToFloat10(bits: Bits): number {
return bitsToFloat(bits, precisionConfigs.custom);
}
利用二元基因组进行大脑功能
之前,我们的大脑函数直接处理十进制形式的engineCoefficients多项式wheelCoefficients系数。然而,这些系数现在以基因组的二进制形式编码。让我们添加一个decodeGenome()从基因组中提取系数的函数,并重写我们的大脑函数:
// Car has 16 distance sensors.
const CAR_SENSORS_NUM = 8;
// Additional formula coefficient that is not connected to a sensor.
const BIAS_UNITS = 1;
// How many genes do we need to encode each numeric parameter for the formulas.
const GENES_PER_NUMBER = precisionConfigs.custom.totalBitsCount;
// Based on 8 distance sensors we need to provide two formulas that would define car's behavior:
// 1. Engine formula (input: 8 sensors; output: -1 (backward), 0 (neutral), +1 (forward))
// 2. Wheels formula (input: 8 sensors; output: -1 (left), 0 (straight), +1 (right))
const ENGINE_FORMULA_GENES_NUM = (CAR_SENSORS_NUM + BIAS_UNITS) * GENES_PER_NUMBER;
const WHEELS_FORMULA_GENES_NUM = (CAR_SENSORS_NUM + BIAS_UNITS) * GENES_PER_NUMBER;
// The length of the binary genome of the car.
const GENOME_LENGTH = ENGINE_FORMULA_GENES_NUM + WHEELS_FORMULA_GENES_NUM;
type DecodedGenome = {
engineFormulaCoefficients: Coefficients,
wheelsFormulaCoefficients: Coefficients,
}
// Converts the genome from a binary form to the decimal form.
const genomeToNumbers = (genome: Genome, genesPerNumber: number): number[] => {
if (genome.length % genesPerNumber !== 0) {
throw new Error('Wrong number of genes in the numbers genome');
}
const numbers: number[] = [];
for (let numberIndex = 0; numberIndex < genome.length; numberIndex += genesPerNumber) {
const number: number = bitsToFloat10(genome.slice(numberIndex, numberIndex + genesPerNumber));
numbers.push(number);
}
return numbers;
};
// Converts the genome from a binary form to the decimal form
// and splits the genome into two sets of coefficients (one set for each muscle).
const decodeGenome = (genome: Genome): DecodedGenome => {
const engineGenes: Gene[] = genome.slice(0, ENGINE_FORMULA_GENES_NUM);
const wheelsGenes: Gene[] = genome.slice(
ENGINE_FORMULA_GENES_NUM,
ENGINE_FORMULA_GENES_NUM + WHEELS_FORMULA_GENES_NUM,
);
const engineFormulaCoefficients: Coefficients = genomeToNumbers(engineGenes, GENES_PER_NUMBER);
const wheelsFormulaCoefficients: Coefficients = genomeToNumbers(wheelsGenes, GENES_PER_NUMBER);
return {
engineFormulaCoefficients,
wheelsFormulaCoefficients,
};
};
// Update brain function for the engine muscle.
export const getEngineMuscleSignal = (genome: Genome, sensors: Sensors): MuscleSignal => {
const {engineFormulaCoefficients: coefficients} = decodeGenome(genome);
const rawBrainSignal = linearPolynomial(coefficients, sensors);
return brainToMuscleSignal(rawBrainSignal);
};
// Update brain function for the wheels muscle.
export const getWheelsMuscleSignal = (genome: Genome, sensors: Sensors): MuscleSignal => {
const {wheelsFormulaCoefficients: coefficients} = decodeGenome(genome);
const rawBrainSignal = linearPolynomial(coefficients, sensors);
return brainToMuscleSignal(rawBrainSignal);
};
自动驾驶汽车问题陈述
☝🏻 所以,最终,我们终于到了将汽车打造为自动泊车的高级问题分解为简单的优化问题——找到
1801 和 0 的最优组合(找到“足够好”的汽车基因组)的地步。听起来很简单,不是吗?
幼稚的方法
我们可以以一种简单的方式解决寻找“足够好”的基因组的问题,并尝试所有可能的基因组合:
[0, ..., 0, 0], 进而...[0, ..., 0, 1], 进而...[0, ..., 1, 0], 进而...[0, ..., 1, 1], 进而...- ...
但是,我们来算一下。假设180每个比特等于0或等于,1那么就有2^180(或1.53 * 10^54)个可能的组合。假设我们需要给15s每辆车一个,看看它是否能成功停车。假设我们可以10一次运行一个汽车模拟。那么我们需要的15 * (1.53 * 10^54) / 10 = 2.29 * 10^54 [seconds]就是7.36 * 10^46 [years]。等待时间相当长。顺便说一句,2.021 * 10^3 [years]基督诞生后,只有 。
遗传方法
我们需要一个更快的算法来找到基因组的最优值。这时遗传算法就派上用场了。我们可能找不到基因组的最优值,但有可能找到它的最优值。而且,更重要的是,我们不需要等待那么长时间。借助进化模拟器,我能够在……之内找到一个相当不错的基因组24 [hours]。
遗传算法基础
遗传算法( GA) 受到自然选择过程的启发,通常依靠交叉、变异和选择等受生物启发的算子来生成优化问题的高质量解决方案。
为汽车寻找“足够好”的基因组合的问题看起来像一个优化问题,因此 GA 很有可能在这里帮助我们。
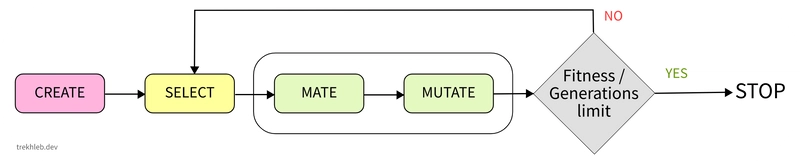
我们不会详细介绍遗传算法,但从高层次上讲,我们需要执行以下基本步骤:
- 创造——第一代汽车不可能凭空而来
180,所以我们会在一开始就生成一组随机的汽车基因组(一组长度为的二进制数组)。例如,我们可以创造~1000汽车。随着种群规模的扩大,找到最优解(并且更快找到)的机会也会增加。 - SELECT - 我们需要从当前代中选出适应度最高的个体进行进一步的交配(参见下一步)。每个个体的适应度将根据适应度函数来定义,在我们的例子中,适应度函数表示汽车距离目标停车位的距离。汽车距离停车位越近,适应度就越高。
- 配对——简单来说,我们允许选定的“♂父车”与选定的“♀母车”进行“交配”,使它们的基因组按一定比例混合,产生“♂♀子车”的基因组。这样做的目的是,通过从父车那里汲取优点(或缺点),子车的自动泊车能力可能会变得更好(或更差)。
~50/50 - 突变- 在交配过程中,一些基因可能会随机突变(子代基因组中的
1s 和s 可能会翻转)。这可能会带来更多子代基因组的多样性,从而带来更多子代汽车行为的多样性。想象一下,如果所有汽车的第一位都被意外地设置为 1,那么测试被设置为 1 的汽车的唯一方法就是通过随机突变。同时,大规模突变可能会破坏健康的基因组。00~10001 - 除非代数达到极限(即已
100过去 代),或者表现最佳的个体已达到预期的适应度函数值(即最佳车辆距离停车位的距离小于1 meter),否则转至“步骤 2”。否则,退出。
利用遗传算法进化汽车的大脑
在启动遗传算法之前,让我们先创建算法的“CREATE”、“SELECT”、“MATE”和“MUTATE”步骤的函数。
CREATE 步骤的函数
该createGeneration()函数将创建一个随机基因组数组(又称种群或世代),并接受两个参数:
generationSize- 定义代的大小。该代的大小将一代一代地保留。genomeLength- 定义汽车种群中每个个体的基因组长度。在我们的例子中,基因组长度为180。
50/50基因组中的每个基因都有可能是0或1。
type Generation = Genome[];
type GenerationParams = {
generationSize: number,
genomeLength: number,
};
function createGenome(length: number): Genome {
return new Array(length)
.fill(null)
.map(() => (Math.random() < 0.5 ? 0 : 1));
}
function createGeneration(params: GenerationParams): Generation {
const { generationSize, genomeLength } = params;
return new Array(generationSize)
.fill(null)
.map(() => createGenome(genomeLength));
}
MUTATE 步骤的函数
该mutate()函数将根据该mutationProbability值随机变异一些基因。
例如,如果 ,mutationProbability = 0.1那么每个基因组都有可能10%发生突变。假设我们有一个长度为 的基因组10,[0, 0, 0, 0, 0, 0 ,0 ,0 ,0 ,0]那么突变后,有 1 个基因可能会发生突变,我们可能会得到一个可能为 的基因组[0, 0, 0, 1, 0, 0 ,0 ,0 ,0 ,0]。
// The number between 0 and 1.
type Probability = number;
// @see: https://en.wikipedia.org/wiki/Mutation_(genetic_algorithm)
function mutate(genome: Genome, mutationProbability: Probability): Genome {
for (let geneIndex = 0; geneIndex < genome.length; geneIndex += 1) {
const gene: Gene = genome[geneIndex];
const mutatedGene: Gene = gene === 0 ? 1 : 0;
genome[geneIndex] = Math.random() < mutationProbability ? mutatedGene : gene;
}
return genome;
}
MATE 步骤的函数
该mate()函数将接受father和mother基因组,并产生两个子代。我们将模拟现实世界的场景,并在交配过程中进行变异。
子代基因组的每个比特位将根据其父代或母代基因组对应比特位的值进行定义。50/50%子代基因组有可能继承父代或母代的比特位。例如,假设我们的基因组长度为4(为了简单起见):
Father's genome: [0, 0, 1, 1]
Mother's genome: [0, 1, 0, 1]
↓ ↓ ↓ ↓
Possible kid #1: [0, 1, 1, 1]
Possible kid #2: [0, 0, 1, 1]
在上面的例子中,突变没有被考虑在内。
以下是函数实现:
// Performs Uniform Crossover: each bit is chosen from either parent with equal probability.
// @see: https://en.wikipedia.org/wiki/Crossover_(genetic_algorithm)
function mate(
father: Genome,
mother: Genome,
mutationProbability: Probability,
): [Genome, Genome] {
if (father.length !== mother.length) {
throw new Error('Cannot mate different species');
}
const firstChild: Genome = [];
const secondChild: Genome = [];
// Conceive children.
for (let geneIndex = 0; geneIndex < father.length; geneIndex += 1) {
firstChild.push(
Math.random() < 0.5 ? father[geneIndex] : mother[geneIndex]
);
secondChild.push(
Math.random() < 0.5 ? father[geneIndex] : mother[geneIndex]
);
}
return [
mutate(firstChild, mutationProbability),
mutate(secondChild, mutationProbability),
];
}
SELECT 步骤的函数
为了选出最适合进一步交配的个体,我们需要一种方法来找出每个基因组的适应度。为此,我们将使用所谓的适应度函数。
适应度函数总是与我们试图解决的具体任务相关,它不是通用的。在我们的例子中,适应度函数将测量汽车与停车位之间的距离。汽车距离停车位越近,适应度就越高。我们稍后会实现适应度函数,但现在,让我们先介绍一下它的接口:
type FitnessFunction = (genome: Genome) => number;
现在,假设我们有种群中每个个体的适应度值。同时假设我们根据适应度值对所有个体进行了排序,使得最靠前的个体是最强的。那么我们应该如何从这个数组中选出父亲和母亲呢?我们需要这样一种选择方式:个体的适应度值越高,被选中交配的几率就越高。该weightedRandom()函数将帮助我们实现这一点。
// Picks the random item based on its weight.
// The items with a higher weight will be picked more often.
const weightedRandom = <T>(items: T[], weights: number[]): { item: T, index: number } => {
if (items.length !== weights.length) {
throw new Error('Items and weights must be of the same size');
}
// Preparing the cumulative weights array.
// For example:
// - weights = [1, 4, 3]
// - cumulativeWeights = [1, 5, 8]
const cumulativeWeights: number[] = [];
for (let i = 0; i < weights.length; i += 1) {
cumulativeWeights[i] = weights[i] + (cumulativeWeights[i - 1] || 0);
}
// Getting the random number in a range [0...sum(weights)]
// For example:
// - weights = [1, 4, 3]
// - maxCumulativeWeight = 8
// - range for the random number is [0...8]
const maxCumulativeWeight = cumulativeWeights[cumulativeWeights.length - 1];
const randomNumber = maxCumulativeWeight * Math.random();
// Picking the random item based on its weight.
// The items with higher weight will be picked more often.
for (let i = 0; i < items.length; i += 1) {
if (cumulativeWeights[i] >= randomNumber) {
return {
item: items[i],
index: i,
};
}
}
return {
item: items[items.length - 1],
index: items.length - 1,
};
};
这个函数的用法非常简单。假设你非常喜欢香蕉,并且比草莓更想吃香蕉。那么你可以调用const fruit = weightedRandom(['banana', 'strawberry'], [9, 1]),在≈9大多数10情况下,变量fruit会等于banana,只有在≈1极少数情况下10,它才会等于strawberry。
为了避免在交配过程中失去最佳个体(我们称之为冠军),我们还可以引入一个所谓的longLivingChampionsPercentage参数。例如,如果longLivingChampionsPercentage = 10,那么10%上一代种群中最好的汽车 将被传承到新一代。你可以想象一下,有些长寿的个体可以长寿,看到它们的子孙后代。
以下是该函数的实际实现select():
// The number between 0 and 100.
type Percentage = number;
type SelectionOptions = {
mutationProbability: Probability,
longLivingChampionsPercentage: Percentage,
};
// @see: https://en.wikipedia.org/wiki/Selection_(genetic_algorithm)
function select(
generation: Generation,
fitness: FitnessFunction,
options: SelectionOptions,
) {
const {
mutationProbability,
longLivingChampionsPercentage,
} = options;
const newGeneration: Generation = [];
const oldGeneration = [...generation];
// First one - the fittest one.
oldGeneration.sort((genomeA: Genome, genomeB: Genome): number => {
const fitnessA = fitness(genomeA);
const fitnessB = fitness(genomeB);
if (fitnessA < fitnessB) {
return 1;
}
if (fitnessA > fitnessB) {
return -1;
}
return 0;
});
// Let long-liver champions continue living in the new generation.
const longLiversCount = Math.floor(longLivingChampionsPercentage * oldGeneration.length / 100);
if (longLiversCount) {
oldGeneration.slice(0, longLiversCount).forEach((longLivingGenome: Genome) => {
newGeneration.push(longLivingGenome);
});
}
// Get the data about he fitness of each individuum.
const fitnessPerOldGenome: number[] = oldGeneration.map((genome: Genome) => fitness(genome));
// Populate the next generation until it becomes the same size as a old generation.
while (newGeneration.length < generation.length) {
// Select random father and mother from the population.
// The fittest individuums have higher chances to be selected.
let father: Genome | null = null;
let fatherGenomeIndex: number | null = null;
let mother: Genome | null = null;
let matherGenomeIndex: number | null = null;
// To produce children the father and mother need each other.
// It must be two different individuums.
while (!father || !mother || fatherGenomeIndex === matherGenomeIndex) {
const {
item: randomFather,
index: randomFatherGenomeIndex,
} = weightedRandom<Genome>(generation, fitnessPerOldGenome);
const {
item: randomMother,
index: randomMotherGenomeIndex,
} = weightedRandom<Genome>(generation, fitnessPerOldGenome);
father = randomFather;
fatherGenomeIndex = randomFatherGenomeIndex;
mother = randomMother;
matherGenomeIndex = randomMotherGenomeIndex;
}
// Let father and mother produce two children.
const [firstChild, secondChild] = mate(father, mother, mutationProbability);
newGeneration.push(firstChild);
// Depending on the number of long-living champions it is possible that
// there will be the place for only one child, sorry.
if (newGeneration.length < generation.length) {
newGeneration.push(secondChild);
}
}
return newGeneration;
}
适应度函数
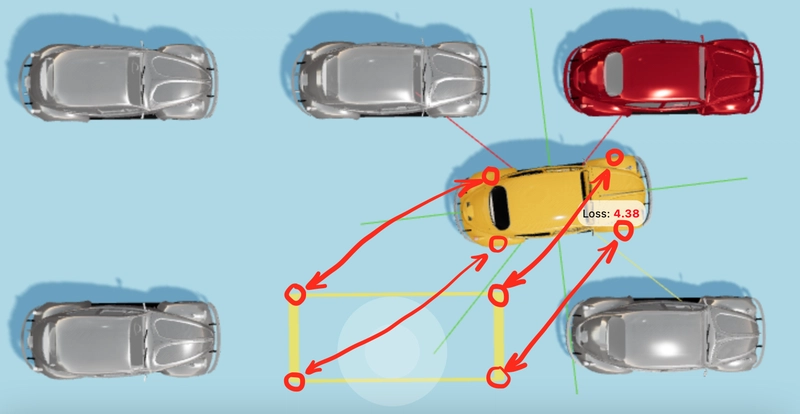
车辆的适应度将由车辆与停车位之间的距离决定。距离越远,适应度越低。
我们最终要计算的距离是4车轮到4停车位对应角落的平均距离。我们将这个距离称为 ,loss它与 成反比fitness。
分别计算每个车轮和每个角之间的距离(而不是仅仅计算从汽车中心到停车位中心的距离)将使汽车保持相对于停车位的正确方向。
空间中两点之间的距离将根据勾股定理计算如下:
type NumVec3 = [number, number, number];
// Calculates the XZ distance between two points in space.
// The vertical Y distance is not being taken into account.
const euclideanDistance = (from: NumVec3, to: NumVec3) => {
const fromX = from[0];
const fromZ = from[2];
const toX = to[0];
const toZ = to[2];
return Math.sqrt((fromX - toX) ** 2 + (fromZ - toZ) ** 2);
};
汽车和停车位之间的距离(loss)将按如下方式计算:
type RectanglePoints = {
fl: NumVec3, // Front-left
fr: NumVec3, // Front-right
bl: NumVec3, // Back-left
br: NumVec3, // Back-right
};
type GeometricParams = {
wheelsPosition: RectanglePoints,
parkingLotCorners: RectanglePoints,
};
const carLoss = (params: GeometricParams): number => {
const { wheelsPosition, parkingLotCorners } = params;
const {
fl: flWheel,
fr: frWheel,
br: brWheel,
bl: blWheel,
} = wheelsPosition;
const {
fl: flCorner,
fr: frCorner,
br: brCorner,
bl: blCorner,
} = parkingLotCorners;
const flDistance = euclideanDistance(flWheel, flCorner);
const frDistance = euclideanDistance(frWheel, frCorner);
const brDistance = euclideanDistance(brWheel, brCorner);
const blDistance = euclideanDistance(blWheel, blCorner);
return (flDistance + frDistance + brDistance + blDistance) / 4;
};
由于fitness应该与成反比,因此loss我们将这样计算:
const carFitness = (params: GeometricParams): number => {
const loss = carLoss(params);
// Adding +1 to avoid a division by zero.
return 1 / (loss + 1);
};
您可以在Evolution Simulator仪表板上看到特定基因组和当前汽车位置的fitness值:loss
启动进化
让我们把进化函数整合起来。我们将“创造世界”,启动进化循环,让时间流逝,让世代进化,让汽车学习如何停车。
为了获取每辆车的适应度值,我们需要在虚拟的 3D 世界中模拟车辆的行为。Evolution Simulator正是为此而生——它在模拟器中运行以下代码,该代码由 Three.js 编写:
// Evolution setup example.
// Configurable via the Evolution Simulator.
const GENERATION_SIZE = 1000;
const LONG_LIVING_CHAMPIONS_PERCENTAGE = 6;
const MUTATION_PROBABILITY = 0.04;
const MAX_GENERATIONS_NUM = 40;
// Fitness function.
// It is like an annual doctor's checkup for the cars.
const carFitnessFunction = (genome: Genome): number => {
// The evolution simulator calculates and stores the fitness values for each car in the fitnessValues map.
// Here we will just fetch the pre-calculated fitness value for the car in current generation.
const genomeKey = genome.join('');
return fitnessValues[genomeKey];
};
// Creating the "world" with the very first cars generation.
let generationIndex = 0;
let generation: Generation = createGeneration({
generationSize: GENERATION_SIZE,
genomeLength: GENOME_LENGTH, // <- 180 genes
});
// Starting the "time".
while(generationIndex < MAX_GENERATIONS_NUM) {
// SIMULATION IS NEEDED HERE to pre-calculate the fitness values.
// Selecting, mating, and mutating the current generation.
generation = select(
generation,
carFitnessFunction,
{
mutationProbability: MUTATION_PROBABILITY,
longLivingChampionsPercentage: LONG_LIVING_CHAMPIONS_PERCENTAGE,
},
);
// Make the "time" go by.
generationIndex += 1;
}
// Here we may check the fittest individuum of the latest generation.
const fittestCar = generation[0];
运行该select()函数后,generation数组将按适应度值降序排列。因此,适应度最高的汽车始终是数组中的第一辆车。
第一代具有随机基因组的汽车将表现如下:
到了第 40 代,汽车开始学习自动停车,并开始靠近停车位:
另一个起点更具挑战性的例子:
汽车在行驶过程中会撞到其他汽车,而且也无法完美地停入停车位,但这只是汽车诞生以来的第 40 代,因此您可以给汽车更多时间去学习。
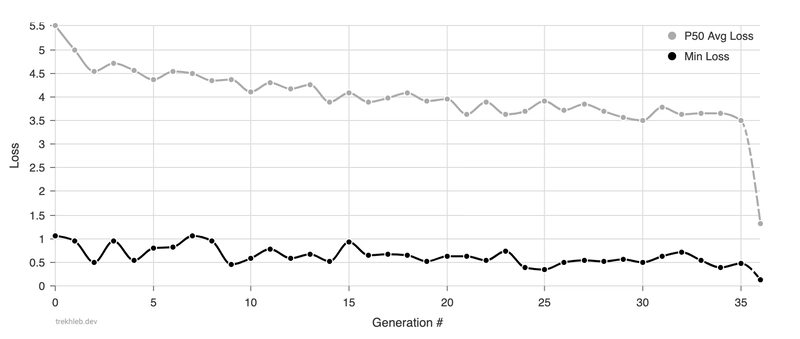
从一代又一代,我们可以看到损失值是如何下降的(这意味着适应度值在上升)。图P50 Avg Loss中显示了适应度最高的车辆的平均损失值(从车辆到停车位的平均距离)50%。图中Min Loss显示了每一代适应度最高的车辆的损失值。
您可能会发现,平均而言,50%这一代适应能力最强的汽车都在学习如何靠近停车位(35代中从5.5m远离停车位到接近停车位3.5m)。数值的变化趋势Min Loss不太明显(从1m到0.5m有一些噪声信号),但从上面的动画中,您可以看到汽车已经学会了一些基本的停车动作。
结论
在本文中,我们将创建自动泊车的高级任务分解为寻找1801 和 0 的最佳组合(寻找最佳汽车基因组)的直接低级任务。
然后,我们应用遗传算法来寻找最优的汽车基因组。它让我们在几个小时的模拟中就获得了相当不错的结果(而不是像之前那样需要多年的运行)。
您可以启动🚕自动泊车进化模拟器,直接在浏览器中查看进化过程。该模拟器为您提供以下功能:
- 您可以从头开始训练汽车并自行调整遗传参数
- 你可能会看到经过训练的自动泊车正在运行
- 您也可以尝试手动停车
本文展示的完整遗传源代码也可以在Evolution Simulator 代码库中找到。如果你是那种会仔细计算并检查代码行数以确保代码行数少于 500 行(不包括测试代码)的人,欢迎随时在这里查看代码🥸。
代码和模拟器仍然存在一些未解决的问题:
- 汽车的“大脑”过于简化,使用线性方程而不是神经网络。这使得汽车无法适应新的环境或新的停车场类型。
- 当一辆车撞上另一辆车时,我们不会降低该车的健康值。因此,该车不会因为造成交通事故而“感到”任何愧疚。
- 进化模拟器并不稳定。这意味着相同的汽车基因组可能会产生不同的适应度值,从而降低进化效率。
- 进化模拟器的性能也非常高,这会减慢进化的进程,因为我们无法同时训练 1000 辆汽车。
- 此外,Evolution Simulator 还需要打开并激活浏览器选项卡才能执行模拟。
- 以及更多...
然而,本文的目的是为了让大家在学习遗传算法的工作原理的同时获得一些乐趣,而不是为了打造一辆可以投入生产的自动泊车特斯拉。所以,即使存在上述问题,我仍然希望您能享受阅读本文的乐趣。
文章来源:https://dev.to/trekhleb/self-parking-car-in-500-lines-of-code-58ea 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com