后端开发教程 - Java、Spring Boot 实战 - msg200.com
Ctrl + F 背后的算法。
chrome 上的 Ctrl + F 会打开一个搜索框，用于在网页、pdf 等上查找文本。这是我见过的最快的搜索框之一，我决定深入研究一下是怎么回事。
那么让我们开始实现快速字符串匹配算法的旅程吧。
注意：我们将要实现的算法可能与 Chrome 中使用的算法类似，但由于我们讨论的是Google ，他们可能已经进行了优化
您可能想知道，当我们有同样功能的正则表达式时，为什么还需要算法？
是的，我们可以使用正则表达式，但是当我们要求它在大数据中寻找模式时，正则表达式会很慢，当我们要求它寻找“动态模式”时，正则表达式非常棒，比如所有以 +91 开头的 10 位电话号码，但在这种情况下，我们想要找到一个特定的字符串。
如果你想了解更多请阅读这里
这就只剩下实现模式匹配器了。让我们从能想到的基本方法开始。给定一个包含数百万个单词的文档，我们想查找一个单词，该怎么做呢？这就像大海捞针。
朴素方法
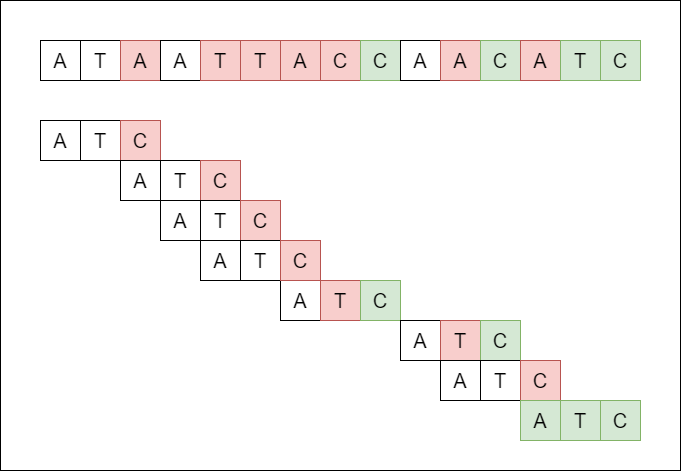
我们想到的第一个想法是逐个字符地比较模式和字符串：
执行 ：
let string = "ATAATTACCAACATC";
let pattern = "ATC";
let position = [];
let found = true;
for(let i=0;i<string.length;i++){
found = true;
for(let j=0;j<pattern.length;j++){
if(string[i+j] != pattern[j]){
found = false;
break;
}
}
if(found){
position.push(i);
}
}
console.log(position);
但这以 O(nm) 的时间复杂度执行，非常慢。
如何优化？
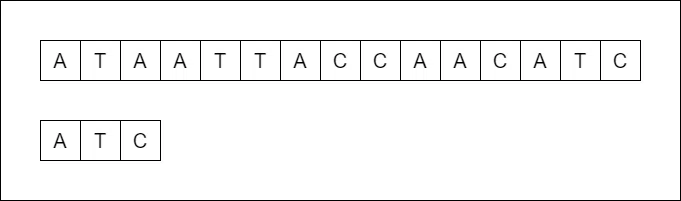
对于每个字符串，如果不匹配，我们就移动一个字符。那么跳过整个单词怎么样？
在这种情况下，当字符串不匹配时，我们不会重新开始，而是跳过该字符串。
在以前的方法中，我们比较了字符串近 45 次，而这里我们只比较了字符串 15 次，这是一个巨大的飞跃。
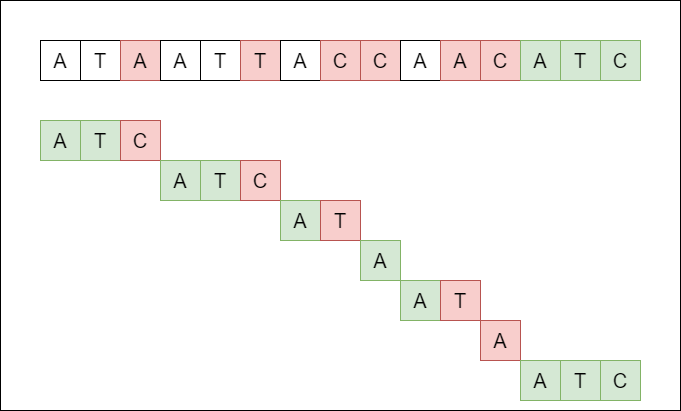
这里我们可以做一个优化，不是从前面比较，而是从后面比较怎么样？
在这种情况下，我们仅比较了字符串 9 次，几乎是前一种情况的一半。
但正如您可能已经猜到的那样，这有一个巨大的缺陷，如果结束字符匹配但起始字符不匹配会怎样？
因此，我们需要一个具体的算法来跳过字符，从而减少整体字符比较。
我们还有什么其他选择？
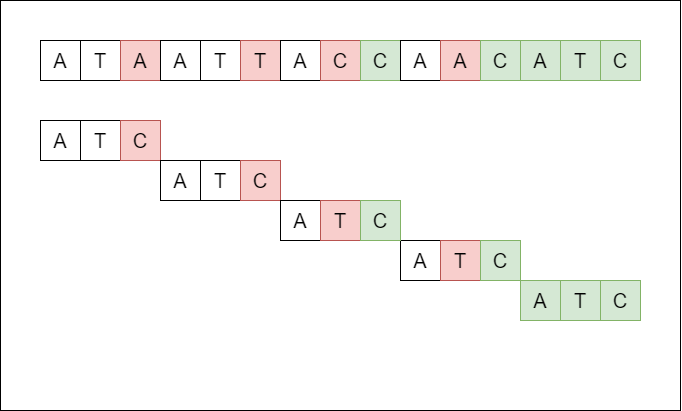
我们可以做的一件事是，不要移动整个图案，而是移动图案的一部分。
我们匹配不匹配的字符串和模式之间的每个字符，然后检查是否有任何共同的字符，如果有，那么我们只移动其中的一部分字符。
在这种情况下，我们进行了 12 次比较操作，如果从任一侧比较字符串和模式，这都会有效。
这个算法被称为Boyer Moore模式匹配算法。
Boyer Moore模式匹配算法的实现
这是原始算法的修改版本，原始算法仅找到模式的第一个实例，而这里我们找到模式的所有出现。
步骤 1> 创建一个大小为 256 的空映射（因为 256 个 ASCII 字符）并设置为 -1。
let string = "ATAATTACCAACATCATAATTACCAACATCATAATTACCAACATCATAATTACCAACATCATC";
let pattern = "ATC";
let M = pattern.length;
let N = string.length;
let skip; //to determine substring skip
let res = []; //to store result
let map = new Array(256); //array of 256 length
步骤 2> 将字符映射到模式中的索引。
for(let c = 0;c<256;c++){
map[c] = -1; //initialize to -1
}
for(let j=0;j<M;j++){
map[pattern[j]] = j; //initialize to the it's index in pattern
}
步骤 3> 循环遍历字符串，注意在 for 循环中，我们使用 i+= skip 而不是“i++”，即跳过字符串的那部分。
for(let i=0;i<=N-M;i+=skip)
步骤4>在每次迭代期间将跳过设置为0，这很重要。
for(let i=0;i<=N-M;i+=skip){
skip=0;
}
步骤 5> 将模式与字符串匹配。
for(let i=0;i<=N-M;i+=skip){
skip=0;
for(let j = M-1;j>=0;j--){
if(pattern[j] != string[i+j]){
skip = Math.max(1,j-map[string[i+j].charCodeAt(0)]);
break;
}
}
}
步骤 6> 如果不匹配，找到必须跳过的长度，在这里我们执行
skip = Math.max(1,j-map[string[i+j]]);
在某些情况下，例如“ACC”和“ATC”，最后一个字符匹配，但其余字符不匹配。
从逻辑上讲，我们必须回溯，将字符串中的第一个“C”与模式中的“C”进行匹配，但这样做意味着我们要回溯，而逻辑上我们不应该这样做，否则我们将陷入无限循环，不断重复。
为了确保匹配过程继续进行，我们确保每当遇到负跳跃的情况时，都将跳跃设置为 1。
步骤 7> 如果跳过为 0，即没有不匹配，则将“i”添加到结果列表中。
if(skip == 0){
console.log(skip)
res.push(i);
skip++;
}
把它们全部结合起来：
let string = "ATAATTACCAACATCATAATTACCAACATCATAATTACCAACATCATAATTACCAACATCATC";
let pattern = "ATC";
let M = pattern.length;
let N = string.length;
let skip;
let res = [];
let map = new Array(256);
for(let c = 0;c<256;c++){
map[c] = -1;
}
for(let j=0;j<M;j++){
map[pattern[j]] = j;
}
for(let i=0;i<=N-M;i+=skip){
skip=0;
for(let j = M-1;j>=0;j--){
if(pattern[j] != string[i+j]){
skip = Math.max(1,j-map[string[i+j].charCodeAt(0)]));
break;
}
}
if(skip == 0){
res.push(i);
skip++;
}
}
console.log(res);
就是这样！这就是 Boyer Moore 模式匹配的工作原理。
还有许多其他模式匹配算法，如Knuth Morris Pratt和Rabin Karp，但它们都有自己的用例。
我在 StackOverflow 上找到了这个，你可以在这里阅读，但简而言之：
Boyer Moore：占用 O(m) 空间，最坏情况为 O(mn)，最好情况为 Ω(m/n)。在词典词汇和长词上的表现比 O(m) 好 25%。实际用例包括 GNU 中用于字符串匹配的 grep 实现，Chrome 很可能使用它进行字符串搜索。
Knuth Morris Pratt：占用 O(m) 空间，最坏情况为 O(m+n)，在 DNA 序列上效果更好。
Rabin Karp：使用 O(1) 辅助空间，这在包含许多长词的文档中搜索长词时表现更好（更多信息请参见 StackOverflow 链接）。
希望你喜欢我的讲解。我通常会写一些关于如何解决面试问题以及算法在实际生活中的应用的文章。
如果我在某个地方搞砸了或者解释错误了某些事情，请在下面评论。
谢谢阅读！:)
github：https://github.com/AKHILP96/Data-Structures-and-Algorithms/blob/master/Algorithm/boyermoore.js
附言：我正在找工作，如果你想找一个懂得如何设计 UI/UX 并且同时兼顾开发的人，请联系我 :) 谢谢！
