破解 40 道 Facebook 编程面试题
在Facebook找到一份工作是全球许多开发者的梦想。Facebook 是全球顶尖的科技公司之一,拥有超过 52,000 名员工。Facebook 以其以成长为导向的公司文化、快速的晋升通道、优厚的福利待遇以及很少有公司能比拟的高薪而闻名。
但竞争异常激烈,随着新员工的激增,Facebook 正在积极寻找顶尖人才。Facebook 看重的是你的文化契合度、通才知识、在有限条件下开发的能力以及专业的编程技能。
为了帮助您做好准备,今天我将介绍破解 Facebook 面试所需的一切,包括编码问题和分步准备指南。
今天我们将讨论:
在 Facebook 面试中取得成功。
通过学习常见问题背后的模式,为 Facebook 面试做好战略准备
Facebook 编程面试概述
要想在 Facebook 找到一份软件工程师的工作,你需要了解未来会发生什么。准备得越充分,你就越有信心。那么,让我们来详细分析一下。想要深入了解 Facebook 的面试流程,请查看 Coding Interviews 提供的免费Facebook 编程面试指南。
- 面试时间:从提交简历到收到工作邀请,整个过程大约需要 1.5 到 2 个月。
- 面试类型:面试流程包含 6 到 7 场面试。其中包括 1 场预筛选面试(20 分钟)、1 场技术电话面试(50 分钟,包含 1-2 个编程问题)以及 4-5 场现场面试(每场 45 分钟)。
- 现场面试: Facebook 将现场面试分为三个部分。忍者部分包含两场使用白板的编程面试。海盗部分包含两场系统设计面试。绝地部分包含一场文化/行为面试。
- 编程题: Facebook 的面试题侧重于算法、数据结构和时间复杂度等通识知识。面试官也会考察架构和系统设计(甚至是入门级)。
- 招聘级别: Facebook 通常招聘 E3 级别的入门级软件职位,E9 级别更高。E5 级别被视为入门级经理职位。
- 招聘团队: Oculus、Facebook Groups 和 WhatsApp 的中心招聘团队。
- 编程语言: Facebook 倾向于大多数标准语言,包括 Java、C++、Python、Ruby 和 Perl。
Facebook 面试有何不同?
系统设计面试:
- 在 Facebook,无论你面试哪个级别,你都会遇到这些问题。
结构化面试:
- Facebook 会将您与担任过您所面试职位的面试官或与直接负责您所面试职位的人员配对。
核心价值观和您的行为面试:
- Facebook 面试官还会评估你体现其五大核心价值观的能力:快速行动、大胆尝试、关注影响力、开放心态和构建社会价值。
Facebook 40 个热门编程面试问题
在本节中,我们将深入探讨40 个最常见的编程面试问题。我们将讨论面试中必然会遇到的 15 个问题的答案和运行时复杂度,并列出 25 个你可能会遇到的问题的最终清单。
每个问题都将在 Python 3 中得到解决。要查看 C++、Ruby、Java 和 JavaScript 中的解决方案,请访问此处。
如果您想自己解决这些问题,请参阅我最初发布的这篇文章,其中有一个交互式代码小部件。
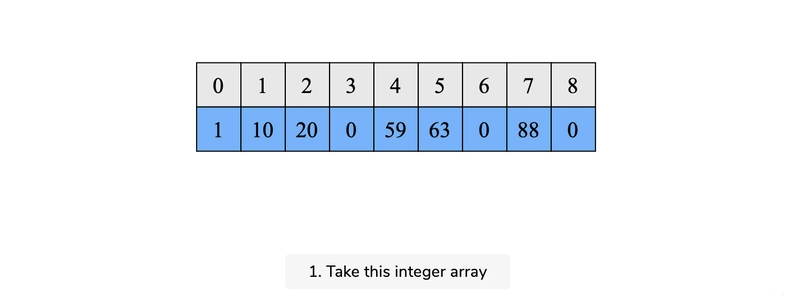
数组:将零移到左侧
给定一个整数数组,将所有 0 元素向左移动,同时保持数组中其他元素的顺序不变。数组必须进行原地修改。
def move_zeros_to_left(A):
if len(A) < 1:
return
lengthA = len(A)
write_index = lengthA - 1
read_index = lengthA - 1
while(read_index >= 0):
if A[read_index] != 0:
A[write_index] = A[read_index]
write_index -= 1
read_index -= 1
while(write_index >= 0):
A[write_index]=0;
write_index-=1
v = [1, 10, 20, 0, 59, 63, 0, 88, 0]
print("Original Array:", v)
move_zeros_to_left(v)
print("After Moving Zeroes to Left: ", v)
运行时复杂度:线性,O(n)
内存复杂度:常数,O(1)
保留两个标记:read_index和write_index,并将它们指向数组的末尾。让我们看一下该算法的概述。
read_index当向数组的起始位置移动时:
- 如果
read_index指向0,则跳过。 - 如果
read_index指向非零值,则将 处的值写入read_index并write_index减少write_index。 - 将 之前的所有值
write_index以及 的当前位置write_index也赋为零。
数组:合并重叠区间
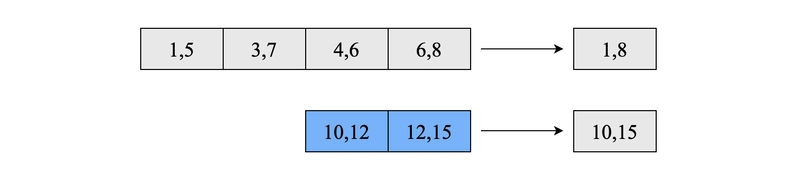
输入一个包含间隔对的数组(列表),每个间隔都有一个起始和结束时间戳。输入数组按起始时间戳排序。你需要合并重叠的间隔并返回一个新的输出数组。
考虑下面的输入数组。区间 (1, 5)、(3, 7)、(4, 6)、(6, 8) 重叠,因此应该合并为一个较大的区间 (1, 8)。同样,区间 (10, 12) 和 (12, 15) 也重叠,应该合并为 (10, 15)。
class Pair:
def __init__(self, first, second):
self.first = first
self.second = second
def merge_intervals(v):
if v == None or len(v) == 0 :
return None
result = []
result.append(Pair(v[0].first, v[0].second))
for i in range(1, len(v)):
x1 = v[i].first
y1 = v[i].second
x2 = result[len(result) - 1].first
y2 = result[len(result) - 1].second
if y2 >= x1:
result[len(result) - 1].second = max(y1, y2)
else:
result.append(Pair(x1, y1))
return result;
v = [Pair(1, 5), Pair(3, 1), Pair(4, 6),
Pair(6, 8), Pair(10, 12), Pair(11, 15)]
result = merge_intervals(v)
for i in range(len(result)):
print("[" + str(result[i].first) + ", " + str(result[i].second) + "]", end =" ")
运行时复杂度:线性,O(n)
内存复杂度:线性,O(n)
这个问题可以用一个简单的线性扫描算法来解决。我们知道输入是按起始时间戳排序的。以下是我们遵循的方法:
- 给出了输入间隔列表,我们将合并的间隔保留在输出列表中。
- 对于输入列表中的每个间隔:
- 如果输入间隔与输出列表中的最后一个间隔重叠,那么我们将合并这两个间隔,并使用合并后的间隔更新输出列表的最后一个间隔。
- 否则,我们将向输出列表中添加一个输入间隔。
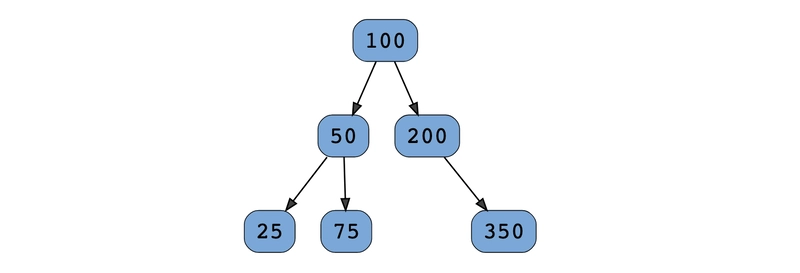
树:将二叉树转换为双向链表
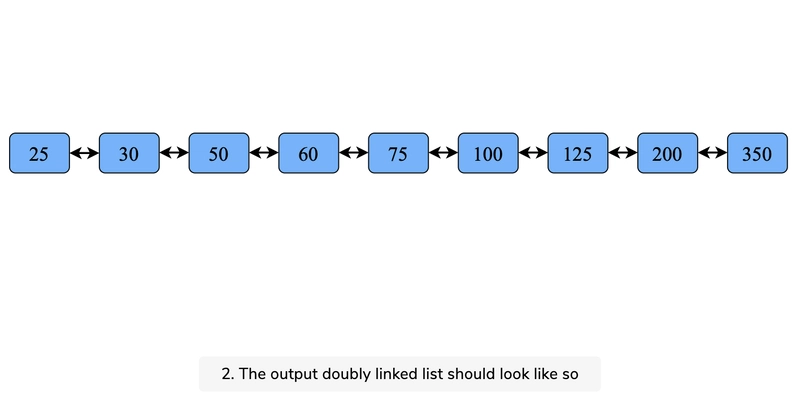
将二叉树转换为双向链表,使得双向链表的顺序与二叉树的中序遍历相同。
转换后,节点的左指针应该指向双向链表中的上一个节点,右指针应该指向双向链表中的下一个节点。在查看答案和解释之前,请先自己尝试一下。
# merge(fuse) two sorted linked lists
def concatenate_lists(head1, head2):
if head1 == None:
return head2
if head2 == None:
return head1
# use left for previous.
# use right for next.
tail1 = head1.left
tail2 = head2.left
tail1.right = head2
head2.left = tail1
head1.left = tail2
tail2.right = head1
return head1
def convert_to_linked_list(root):
if root == None:
return None
list1 = convert_to_linked_list(root.left)
list2 = convert_to_linked_list(root.right)
root.left = root.right = root
result = concatenate_lists(list1, root)
result = concatenate_lists(result, list2)
return result
def get_list(head):
r = []
if head == None:
return r
temp = head
while True:
r.append(temp.data)
temp = temp.right
if temp == head:
break
return r
def test(orig_data):
root = create_BST(orig_data)
all_data = bst_to_list(root)
#print(all_data);
head = convert_to_linked_list(root)
#print_list(all_data)
#print_list(v)
return head
def main():
data = [100,50,200,25,75,350]
res = test(data)
v = get_list(res)
print_list(v)
main()
运行时复杂度:线性,O(n)
内存复杂度:线性,O(h)。
在中序遍历中,首先遍历左子树,然后访问根,最后遍历右子树。
解决这个问题的一个简单方法是从一个空的双向链表开始。在对二叉树进行中序遍历的同时,不断将每个元素输出插入到双向链表中。
但是,如果我们仔细看问题,面试官希望我们将二叉树就地转换为双向链表,即我们不应该为双向链表创建新节点。
这个问题可以用分治法递归解决。具体算法如下。
- 从根节点开始,递归求解左子树和右子树
- 在每个步骤中,一旦处理了左子树和右子树:
- 将左子树的输出与根融合,得到中间结果
- 将中间结果(在上一步中构建)与右子树的输出融合,以得出当前递归调用的最终结果。
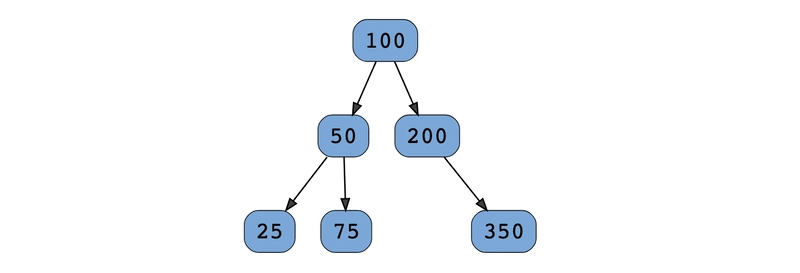
树:二叉树的层序遍历
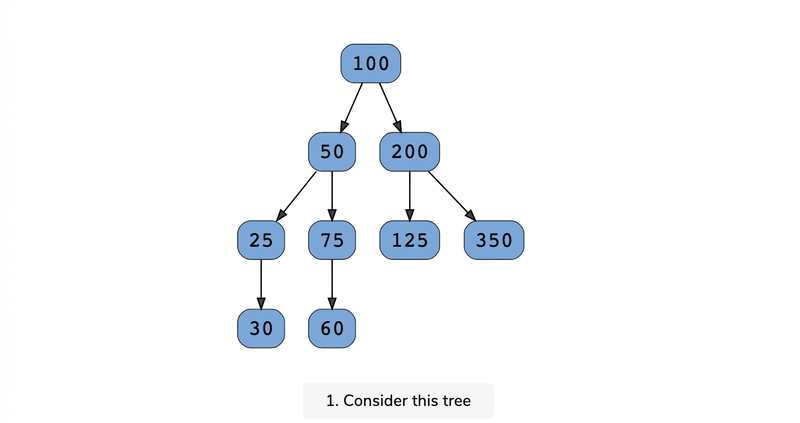
给定一棵二叉树的根节点,请显示每一层的节点值。所有层的节点值应分别显示在不同的行上。我们来看看下面的二叉树。
这棵树的层序遍历应该如下所示:
- 100
- 50, 200
- 25、75、350
# Using two queues
def level_order_traversal_1(root):
if root == None:
return
queues = [deque(), deque()]
current_queue = queues[0]
next_queue = queues[1]
current_queue.append(root)
level_number = 0
while current_queue:
temp = current_queue.popleft()
print(str(temp.data) , end = " ")
if temp.left != None:
next_queue.append(temp.left)
if temp.right != None:
next_queue.append(temp.right)
if not current_queue:
print()
level_number += 1
current_queue = queues[level_number % 2]
next_queue = queues[(level_number + 1) % 2]
print()
arr = [100,50,200,25,75,350]
root = create_BST(arr)
print("InOrder Traversal:", end = "")
display_inorder(root)
print("\nLevel Order Traversal:\n", end = "")
level_order_traversal_1(root)
运行时复杂度:线性,O(n)
内存复杂度:线性,O(n)
这里,你使用了两个队列:current_queue和next_queue。你根据当前的层级编号交替地将节点推送到两个队列中。
你将从 中出队节点current_queue,打印节点的数据,并将节点的子节点入队到next_queue。
一旦current_queue变为空,就表示当前 的所有节点都已处理完毕level_number。为了指示新的级别,请打印换行符 ( \n),交换两个队列,然后继续上述逻辑。
打印完 中的叶节点后current_queue,交换current_queue和next_queue。由于current_queue为空,因此可以终止循环。
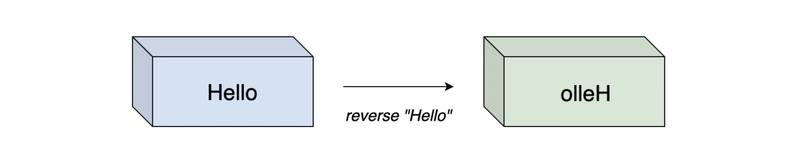
字符串:反转句子中的单词
反转给定句子(字符数组)中单词的顺序。以“Hello World”字符串为例:
def str_rev(str, start, end):
if str == None or len(str) < 2:
return
while start < end:
temp = str[start]
str[start] = str[end]
str[end] = temp
start += 1
end -= 1
def reverse_words(sentence):
# Here sentence is a null-terminated string ending with char '\0'.
if sentence == None or len(sentence) == 0:
return
# To reverse all words in the string, we will first reverse
# the string. Now all the words are in the desired location, but
# in reverse order: "Hello World" -> "dlroW olleH".
str_len = len(sentence)
str_rev(sentence, 0, str_len - 2)
# Now, let's iterate the sentence and reverse each word in place.
# "dlroW olleH" -> "World Hello"
start = 0
end = 0
while True:
# find the start index of a word while skipping spaces.
while start < len(sentence) and sentence[start] == ' ':
start += 1
if start == str_len:
break
# find the end index of the word.
end = start + 1
while end < str_len and sentence[end] != ' ':
end += 1
# let's reverse the word in-place.
str_rev(sentence, start, end - 1)
start = end
def get_array(t):
s = array('u', t)
return s
def print_array(s):
i = 0
while i != len(s):
stdout.write(s[i])
i += 1
print ()
s = get_array('Hello World!')
print_array(s)
reverse_words(s)
print_array(s)
该解决方案的工作原理如下:
- 反转字符串。
- 遍历字符串并反转每个单词。
有关字符串反转的更多信息,请阅读我的文章“在 JavaScript、C++ 和 Python 中反转字符串的最佳实践”。
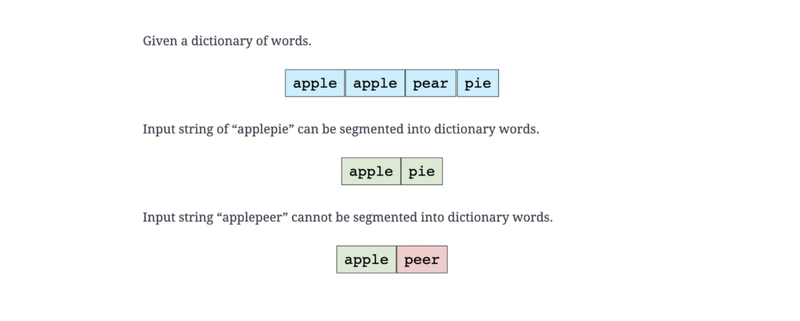
字符串:字符串分割
给定一本词典和一个较大的输入字符串。你需要判断输入字符串能否完全分割成给定词典中的单词。以下示例将进一步阐述这个问题。
def can_segment_string(s, dictionary):
for i in range(1, len(s) + 1):
first = s[0:i]
if first in dictionary:
second = s[i:]
if not second or second in dictionary or can_segment_string(second, dictionary):
return True
return False
s = "hellonow";
dictionary= set(["hello","hell","on","now"])
if can_segment_string(s, dictionary):
print("String Can be Segmented")
else:
print("String Can NOT be Segmented")
运行时复杂度:指数,O(2^n),如果我们只使用递归。
内存复杂度:多项式,O(n^2)
您可以通过在每个可能的位置对大字符串进行分割来解决这个问题,看看该字符串是否可以完全分割成字典中的单词。如果您将算法分步编写,则如下所示:
n = length of input string
for i = 0 to n - 1
first_word = substring (input string from index [0, i] )
second_word = substring (input string from index [i + 1, n - 1] )
if dictionary has first_word
if second_word is in dictionary OR second_word is of zero length, then return true
recursively call this method with second_word as input and return true if it can be segmented
该算法将在循环的每次迭代中从头计算两个字符串。最坏的情况是,second_word每次迭代都会进行一次递归调用。这会使时间复杂度飙升至 2^n。
你会发现,即使字典中不存在同一个子字符串,你也可能多次计算它。这种冗余可以通过记忆化来解决,即记住哪些子字符串已经被解析过。
为了实现记忆化,你可以second每次将字符串存储在一个新集合中。这将减少时间和内存复杂度。
动态规划:寻找最大单笔销售利润
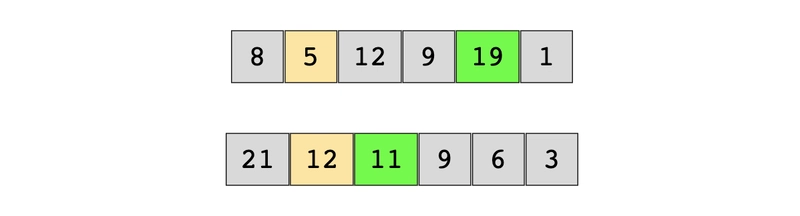
给定每日股票价格列表(为简单起见,使用整数),返回可获得最大利润的买入价和卖出价。
我们需要最大化单笔买入/卖出的利润。如果无法盈利,我们会尽量减少损失。以下示例中,最大利润的买入价(橙色)和卖出价(绿色)已突出显示。
current_buy = array[0]
global_sell = array[1]
global_profit = global_sell - current_buy
current_profit = -sys.maxsize - 1
for i in range(1, len(array)):
current_profit = array[i] - current_buy
if current_profit > global_profit:
global_profit = current_profit
global_sell = array[i]
if current_buy > array[i]:
current_buy = array[i];
result = global_sell - global_profit, global_sell
return result
array = [1, 2, 3, 4, 3, 2, 1, 2, 5]
result = find_buy_sell_stock_prices(array)
print("Buy Price: " + str(result[0]) + ", Sell Price: " + str(result[1]))
运行时复杂度:线性,O(n)
内存复杂度:常数,O(1)
数组中的值代表股票每天的价格。由于我们只能buy买入sell股票一次,因此我们需要找到在给定时间范围内,使利润最大化(或损失最小化)的最佳价格buy。sell
一个简单的解决方案,运行时复杂度为 $O(n^{2})$,是找到每个元素与其后续元素之间的最大增益。
这个问题有一个棘手的线性解决方案,需要维护current_buy_price(这是迄今为止看到的最小数字),current_profit并且global_profit我们遍历整个股票价格数组。
在每次迭代中,我们将current_profit与进行比较global_profit并相应地更新global_profit。
基本算法如下:
current profit = INT_MIN
current buy = stock_prices[0]
global sell = stock_prices[1]
global profit = global sell - current buy
for i = 1 to stock_prices.length:
current profit = stock_prices[i] - current buy
if current profit is greater than global profit
then update global profit to current profit and update global sell to stock_prices[i]
if stock_prices[i] is less than current buy
then update current buy to stock_prices[i]
return global profit and global sell
数学和统计:计算数字的幂
给定一个双精度数x和一个整数 ,n编写一个函数计算 的幂x。n例如:
幂(2, 5)= 32
幂(3,4)= 81
幂(1.5, 3)= 3.375
幂(2,-2)= 0.25
def power_rec(x, n):
if n == 0:
return 1
if n == 1:
return x
temp = power_rec(x, n//2)
if n % 2 == 0:
return temp * temp
else:
return x * temp * temp
def power(x, n):
is_negative = False
if n < 0:
is_negative = True
n *= -1
result = power_rec(x, n)
if is_negative:
return 1 / result
return result
def main():
pass_count = 0
fail_count = 0
for x in range(-10, 5, 1):
for n in range(-4, 6):
if x == 0 and n < 0:
continue
r1 = power(x * 1.0, n)
r2 = pow(x, n)
diff = r1 - r2
if diff < 0:
diff *= -1
if diff > 0.0000000001:
msg = "r1 = %f, r2 = %f, difference = %f" % (r1, r2, diff)
print("Failed for (%d, %d) - %s" % (x, n, msg))
fail_count += 1
else:
pass_count += 1
assert diff <= 0.0000000001
main()
print(pow(2, 5))
运行时复杂度:对数,O(log n)
内存复杂度:对数,O(log n)
这个问题的一个简单算法是乘以x次数n。该算法的时间复杂度为 O(n)。我们可以使用分治法来更有效地解决这个问题。
在除法步骤中,我们不断递归n除法,2直到达到基准情况,即n == 1
r在组合步骤中,我们得到子问题的结果,并使用以下两个规则计算当前问题的结果:
- 如果 n 为偶数,则结果为 r * r(其中 r 是子问题的结果)
- 如果 n 为奇数,则结果为 x * r * r(其中 r 是子问题的结果)。
回溯:找到所有可能的子集
我们得到一组整数,我们必须找到这组整数的所有可能的子集。
def get_bit(num, bit):
temp = (1 << bit)
temp = temp & num
if temp == 0:
return 0
return 1
def get_all_subsets(v, sets):
subsets_count = 2 ** len(v)
for i in range(0, subsets_count):
st = set([])
for j in range(0, len(v)):
if get_bit(i, j) == 1:
st.add(v[j])
sets.append(st)
def main():
v = [8,13,3,22,17,39,87,45,36]
subsets = []
get_all_subsets(v, subsets);
print("****Total*****" + str(len(subsets)))
for i in range(0, len(subsets)):
print("{", end = "")
print(subsets[i], end = "")
print("}")
print("****Total*****" + str(len(subsets)))
main()
运行时复杂度:指数级,O(2^n * n),其中 $n$ 是给定集合中的整数数量
内存复杂度:常数,O(2^n * n)
有几种方法可以解决这个问题。我们将讨论一种简洁易懂的方法。我们知道,一个包含 n 个元素的集合有 2^n 个子集。例如,一个包含 3 个元素的集合就有 8 个子集。我们将使用的算法如下:
n = size of given integer set
subsets_count = 2^n
for i = 0 to subsets_count
form a subset using the value of 'i' as following:
bits in number 'i' represent index of elements to choose from original set,
if a specific bit is 1 choose that number from original set and add it to current subset,
e.g. if i = 6 i.e 110 in binary means that 1st and 2nd elements in original array need to be picked.
add current subset to list of all subsets
请注意,从集合中挑选整数的位顺序并不重要;从左到右挑选整数将产生与从右到左挑选整数相同的输出。
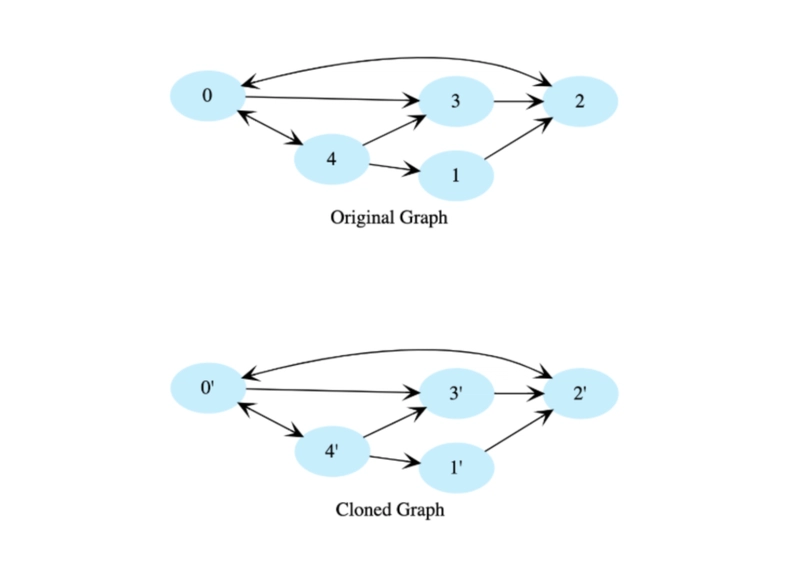
图表:克隆有向图
给定有向图的根节点,通过创建其深度副本来克隆该图,以便克隆的图具有与原始图相同的顶点和边。
让我们以下面的图为例。如果输入图为 G = (V, E),其中 V 是顶点集合,E 是边集合,则输出图(克隆图)G' = (V', E'),其中 V = V',E = E'。
注意:我们假设所有顶点都可以从根顶点到达。即我们有一个连通图。
class Node:
def __init__(self, d):
self.data = d
self.neighbors = []
def clone_rec(root, nodes_completed):
if root == None:
return None
pNew = Node(root.data)
nodes_completed[root] = pNew
for p in root.neighbors:
x = nodes_completed.get(p)
if x == None:
pNew.neighbors += [clone_rec(p, nodes_completed)]
else:
pNew.neighbors += [x]
return pNew
def clone(root):
nodes_completed = {}
return clone_rec(root, nodes_completed)
# this is un-directed graph i.e.
# if there is an edge from x to y
# that means there must be an edge from y to x
# and there is no edge from a node to itself
# hence there can maximim of (nodes * nodes - nodes) / 2 edgesin this graph
def create_test_graph_undirected(nodes_count, edges_count):
vertices = []
for i in range(0, nodes_count):
vertices += [Node(i)]
all_edges = []
for i in range(0, nodes_count):
for j in range(i + 1, nodes_count):
all_edges.append([i, j])
shuffle(all_edges)
for i in range(0, min(edges_count, len(all_edges))):
edge = all_edges[i]
vertices[edge[0]].neighbors += [vertices[edge[1]]]
vertices[edge[1]].neighbors += [vertices[edge[0]]]
return vertices
def print_graph(vertices):
for n in vertices:
print(str(n.data), end = ": {")
for t in n.neighbors:
print(str(t.data), end = " ")
print()
def print_graph_rec(root, visited_nodes):
if root == None or root in visited_nodes:
return
visited_nodes.add(root)
print(str(root.data), end = ": {")
for n in root.neighbors:
print(str(n.data), end = " ")
print("}")
for n in root.neighbors:
print_graph_rec(n, visited_nodes)
def print_graph(root):
visited_nodes = set()
print_graph_rec(root, visited_nodes)
def main():
vertices = create_test_graph_undirected(7, 18)
print_graph(vertices[0])
cp = clone(vertices[0])
print()
print("After copy.")
print_graph(cp)
main()
运行时复杂度:线性 O(n)
内存复杂度:对数,O(log n)
我们使用深度优先遍历,并在遍历图时创建每个节点的副本。为了避免陷入循环,我们将使用哈希表来存储每个已完成的节点,并且不会重复访问哈希表中已存在的节点。
哈希表的键将是原始图中的一个节点,其值将是克隆图中的相应节点。
设计:序列化/反序列化二叉树
将二叉树序列化为文件,然后将其反序列化回树,以便原始树和反序列化的树相同。
- 序列化:将树写入文件中。
- 反序列化:从文件中读取并在内存中重建树。
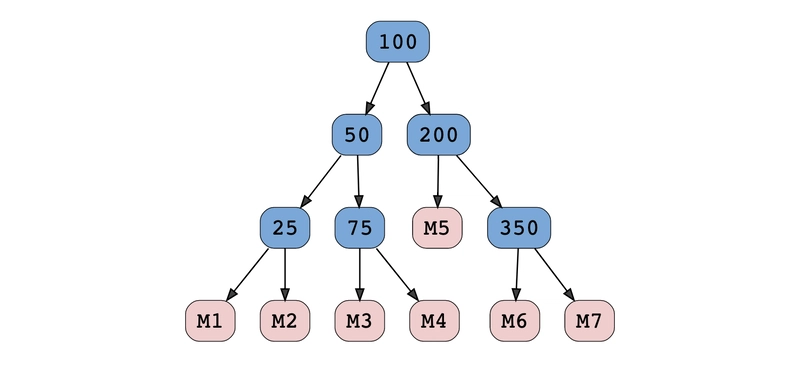
序列化流的格式没有限制,因此您可以用任何高效的格式对其进行序列化。但是,从流中反序列化树后,它应该与原始树完全相同。请考虑以下树作为输入树。
MARKER = sys.maxsize
def serialize(node, stream):
if node == None:
stream.dump(MARKER);
return
stream.dump(node.data);
serialize(node.left, stream)
serialize(node.right, stream)
def deserialize(stream):
try:
data = pickle.load(stream)
if data == MARKER:
return None
node = BinaryTreeNode(data);
node.left = deserialize(stream)
node.right = deserialize(stream)
return node
except pickle.UnpicklingError:
return None
root = create_random_BST(15)
display_level_order(root)
output = open('data.class', 'wb')
p = pickle.Pickler(output)
serialize(root, p)
output.close()
input2 = open('data.class','rb')
root_deserialized = deserialize(input2)
display_level_order(root_deserialized)
assert is_identical_tree(root, root_deserialized), "Trees should be identical"
运行时复杂度:线性 O(n)
内存复杂度:对数,O(log n)
序列化和反序列化树的方法有很多种。一种方法是执行深度优先遍历,并将各个节点序列化到流中。这里我们将使用前序遍历。我们还将序列化一些标记以表示空指针,以帮助反序列化树。
以下面的二叉树为例。这棵树中添加了标记 (M*) 来表示空节点。每个标记对应的数字(例如 M1 中的 1,M2 中的 2)仅表示标记在流中的相对位置。
在反序列化树时,我们再次使用前序遍历,并为每个非标记节点创建一个新节点。遇到标记节点则表示它是一个空节点。
排序和搜索:查找最高和最低索引
给定一个已排序的整数数组,返回给定键的低索引和高索引。如果未找到索引,则必须返回 -1。
数组长度可能达到数百万,并且包含许多重复项。
在以下示例中,根据key,low和high索引将是:
key:1,low= 0 和high= 0key:2,low= 1 和high= 1key:5,low= 2 和high= 9key:20,low= 10 和high= 10
为了测试您的代码,输入数组将是:
1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 6, 6
现在来看看解决方案。
def find_low_index(arr, key):
low = 0
high = len(arr) - 1
mid = int(high / 2)
while low <= high:
mid_elem = arr[mid]
if mid_elem < key:
low = mid + 1
else:
high = mid - 1
mid = low + int((high - low) / 2)
if low < len(arr) and arr[low] == key:
return low
return -1
def find_high_index(arr, key):
low = 0
high = len(arr) - 1
mid = int(high / 2)
while low <= high:
mid_elem = arr[mid]
if mid_elem <= key:
low = mid + 1
else:
high = mid - 1
mid = low + int((high - low) / 2);
if high == -1:
return high
if high < len(arr) and arr[high] == key:
return high
return -1
array = [1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 6, 6]
key = 5
low = find_low_index(array, key)
high = find_high_index(array, key)
print("Low Index of " + str(key) + ": " + str(low))
print("High Index of " + str(key) + ": " + str(high))
key = -2
low = find_low_index(array, key)
high = find_high_index(array, key)
print("Low Index of " + str(key) + ": " + str(low))
print("High Index of " + str(key) + ": " + str(high))
运行时复杂度:对数 O(log n)
内存复杂度:常数,O(1)
由于数组大小可能高达数百万,因此对已排序数组进行线性扫描查找low和high索引效率极低。因此,我们将使用略微改进的二分查找法来查找给定键的low和索引。 我们需要进行两次二分查找:high
- 一次用于查找
low索引。 - 一次用于查找
high索引。
低指数
让我们看一下查找low索引的算法:
low在每一步中,考虑和索引之间的数组high并计算mid索引。- 如果索引处的元素
mid小于key,low则变为mid + 1(向范围的开始移动)。 - 如果 mid 处的元素大于或等于
key,则high变为mid - 1。 处的索引low保持不变。 - 当
low大于时high,low将指向第一次出现的key。 - 如果 处的元素
low与 不匹配key,则返回-1。
高指数
类似地,我们可以high通过稍微修改上述条件来找到索引:
- 当索引处的元素小于或等于时,将索引切换
low为。mid + 1midkey - 当 处的元素大于时,将索引切换
high到。mid - 1midkey
排序和搜索:搜索旋转数组
在一个已排序的数组中,查找元素唯一且按任意数旋转后的数字。-1如果不存在,则返回该数字。
假设数组不包含重复项
任务是在这个数组中找到给定的数字。
def binary_search(arr, start, end, key):
# assuming all the keys are unique.
if (start > end):
return -1;
mid = int(start + (end - start) / 2)
if arr[mid] == key:
return mid
if arr[start] <= arr[mid] and key <= arr[mid] and key >= arr[start]:
return binary_search(arr, start, mid - 1, key)
elif arr[mid] <= arr[end] and key >= arr[mid] and key <= arr[end]:
return binary_search(arr, mid + 1, end, key)
elif arr[end] <= arr[mid]:
return binary_search(arr, mid + 1, end, key)
elif arr[start] >= arr[mid]:
return binary_search(arr, start, mid - 1, key)
return -1;
def binary_search_rotated(arr, key):
return binary_search(arr, 0, len(arr)-1, key)
v1 = [6, 7, 1, 2, 3, 4, 5];
print("Key(3) found at: " + str(binary_search_rotated(v1, 3)))
print("Key(6) found at: " + str(binary_search_rotated(v1, 6)))
v2 = [4, 5, 6, 1, 2, 3];
print("Key(3) found at: " + str(binary_search_rotated(v2, 3)))
print("Key(6) found at: " + str(binary_search_rotated(v2, 6)))
运行时复杂度:对数,O(log n)
内存复杂度:对数,O(log n)
该解决方案本质上是二分查找,但进行了一些修改。如果我们仔细观察示例中的数组,我们会注意到数组中至少有一半是有序的。我们可以利用这个特性来发挥它的优势。
如果数字n位于数组已排序的那一半内,那么我们的问题就是一个基本的二分查找。否则,丢弃已排序的那一半,继续检查未排序的那一半。由于我们每一步都将数组分成两半,因此运行时复杂度为 O(log n)。
25 个常见的 Facebook 编程面试问题
- 整数数组的最长递增子序列(动态规划数组)
- 网格中的唯一路径(动态规划矩阵)
- 将两个数字添加为列表(列表)
- 设计缓存(系统设计)
- 设计高度一致的数据库(系统设计)
- 旋转矩阵(数组)
- 设计一个 URL 缩短器(系统设计)
- 设计推荐系统(ML,系统设计)
- 查找第 n 个斐波那契数(数论)
- 使用二分查找法找到整数的平方根(数学搜索答案)
- 实现
StrStr(字符串搜索) - 回文(字符串)的最小附加
- 找到直方图中最大的矩形(堆栈)
- 子字符串连接(增量哈希)
- 找到最小共同祖先(树搜索)
- 查找树中节点之间的最大距离(DFS)
- 找出数组中所有唯一的三元组,得出和为零(数组)
- 求非空二叉树(二叉树)中的最大路径和
- 查找平面上点列表中距离原点最近的 K 个点(搜索/排序)
- 编写一个函数来计算数组的交集(排序/搜索)
- 设计一个打字头功能(系统设计)
- 设计 Facebook Messenger(系统设计)
- 将字母重排组合到字符串数组中(数组/字符串)
- 将 BST 转换为排序循环双向链表(树)
- 确定字典中字母的顺序(图/树)
如何准备 Facebook 面试
现在您已经了解了面试的大概内容,也知道了面试官会问哪些问题,接下来让我们根据 Facebook 独特的面试流程来学习一些准备策略。
准备好你的简历。
你首先应该更新你的简历,使其以指标/可交付成果为导向。同时,展示你所做的工作如何转化为他们的五大核心价值观也是一个好主意:快速行动、勇于创新、关注影响力、保持开放和创造社会价值。
练习通用编码问题
我建议至少三个月的自学才能成功。这包括选择编程语言、复习基础知识,以及学习算法、数据结构、系统设计、面向对象编程等等。
使用不同的工具练习编码很重要:
- 简单的文本编辑器(如 CoderPad)
- 手工书写(在白板或纸上)
- 您喜欢的编码风格
想要一份完整的 12 周面试指南,请查看我们的文章《3 个月的编码面试准备训练营》
准备系统设计面试
设计面试通常不涉及任何编程,所以你需要学习如何回答这些问题。面试时会在白板上进行,所以请用手写练习你的设计。学习系统设计和产品设计。
掌握系统设计问题的最佳方法不是死记硬背答案,而是学习系统设计问题的结构。你需要训练自己从头开始思考,同时考虑规模和需求。
专业提示:如果您想在系统设计面试中脱颖而出,您需要讨论如何在您的设计中实现机器学习。
Facebook 需要下一代工程师,他们高度重视人工智能。不妨考虑复习一下机器学习概念和机器学习系统设计原则。
掌握最佳实践
一旦您掌握了基础知识并按照面试准备路线图取得进展,就可以掌握最佳实践。
练习时,要学会大声清晰地表达你的思路。Facebook 非常在意你的思维方式。编写代码时,要像房间里有其他人一样,解释你的思维过程。
你也应该开始给自己计时,学习如何有效地管理时间。花时间规划你的答案总比直接用蛮力回答要好。
准备行为面试
Facebook 非常重视你是否适合他们的公司,所以你需要做好准备,介绍一下自己。针对 Facebook 的每项价值观,请集思广益,思考你如何融入其中,以及这些价值观对你的重要性。
您还应该考虑自己作为工程师的 2 到 4 年的职业抱负、兴趣和优势,因为它们很可能会在面试中被提及。
要了解如何准备,请查看我的文章《行为面试:如何准备和回答面试问题》
为面试官准备问题
Facebook 重视积极主动的人,所以准备好面试官可能会问的问题非常重要。每次面试你都有时间提出自己的问题。这也是一个机会,让你判断 Facebook 是否适合你的生活方式和需求。
总结和资源列表
破解 Facebook 编码面试取决于您花在准备上的时间,例如练习编码问题、研究行为面试以及了解 Facebook 的公司文化。
虽然没有万能的入场券,但充分的准备一定会让你成为更自信、更理想的候选人。以下重要资源将帮助你准备 Facebook 面试,并建立自信。
继续学习和研究!
 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com