动态规划——解决任何DP面试问题的7个步骤

动态规划——解决任何DP面试问题的7个步骤

动态规划——解决任何DP面试问题的7个步骤

最初发布于Refdash 博客。Refdash 是一个面试平台，帮助工程师与来自 Google、Facebook 或 Palantir 等顶级公司的资深工程师进行匿名面试，并获得详细的反馈。Refdash还帮助工程师根据他们的技能和兴趣发现绝佳的工作机会。

尽管拥有丰富的软件产品开发经验，许多工程师一想到要参加以算法为重点的编程面试，就会感到忐忑不安。我面试过数百名工程师，其中最让工程师感到不安的问题往往与动态规划 (DP) 有关。

许多科技公司喜欢在面试中问DP问题。虽然我们或许可以争论这些问题是否能有效评估一个人胜任工程职位的能力，但DP仍然是工程师在寻找自己喜欢的工作时容易遇到的一个障碍。

动态规划——可预测且可准备

我个人认为DP题目可能不是测试工程能力的最佳方法，原因之一是它们的可预测性，而且容易模式匹配。它们让我们更多地筛选准备程度，而不是工程质量。

这些问题通常表面上看起来很复杂，可能会让你觉得解答这些问题的人非常擅长算法。同样，那些无法理解动态规划中一些令人费解的概念的人，他们的算法知识可能看起来相当薄弱。

现实情况有所不同，而表现的关键在于准备。所以，让我们确保每个人都做好准备，一劳永逸。

解决动态规划问题的最大因素是准备。

解决动态规划问题的 7 个步骤

在本文的其余部分，我将介绍一个方法，您可以按照它来判断一个问题是否是“DP问题”，并找到此类问题的解决方案。具体来说，我将遵循以下步骤：

1. 如何识别DP问题
2. 识别问题变量
3. 清晰地表达递归关系
4. 确定基本情况
5. 决定是否要以迭代或递归方式实现它
6. 添加记忆
7. 确定时间复杂度

DP 问题示例

为了便于理解我将要进行的抽象，我先介绍一个示例问题。在每一节中，我都会参考该问题，但你也可以独立于问题本身阅读其他章节。

问题陈述：

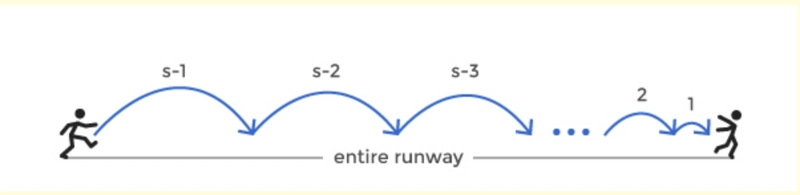
在这个问题中，我们就像在一个疯狂跳跃的球上，试图停下来，同时避开沿途的尖刺。

规则如下：

1) 给定一条平坦的跑道，跑道上布满了尖刺。跑道由一个布尔数组表示，该数组指示特定（离散）点是否没有尖刺。True 表示没有尖刺，False 表示没有尖刺。

数组表示示例

2) 给定一个起始速度 S。S 在任何给定点都是一个非负整数，它表示您下次跳跃时将向前移动多少。

3) 每次着陆在一个点上时，你可以在下一次跳跃之前调整速度最多 1 个单位。

4) 你想安全地停在跑道上的任何地方（不必停在数组的末端）。当你的速度变为 0 时，你就停下来。但是，如果你在任何一点落在尖刺上，你疯狂弹跳的球就会爆裂，游戏就结束了。

函数的输出应该是一个布尔值，指示我们是否可以安全地在跑道上的任何地方停下来。

第一步：如何识别动态规划问题

首先，我们要明确一点，DP 本质上只是一种优化技术。DP 是一种解决问题的方法，它将问题分解成一系列更简单的子问题，每个子问题只需求解一次，并存储它们的解。下次遇到相同的子问题时，我们只需查找之前计算的解，而无需重新计算。这种方法节省了计算时间，但存储空间（希望如此）的开销却很小。

认识到一个问题可以用动态规划求解是解决问题的第一步，通常也是最困难的一步。你需要问自己，你的问题解是否可以表示为类似较小问题解的函数。

就我们的例子问题而言，给定跑道上的一个点、一个速度以及前方跑道，我们就能确定下一步可能跳伞的地点。此外，我们能否以当前速度从当前点停下来，似乎只取决于我们能否从我们选择的下一个地点停下来。这很棒，因为向前移动可以缩短前方的跑道，缩小问题的范围。我们应该能够一直重复这个过程，直到到达一个显而易见是否可以停下来的点。

识别动态规划问题通常是解决该问题最困难的一步。问题解能否表示为类似较小问题解的函数？

第 2 步：识别问题变量

现在我们已经确定子问题之间存在某种递归结构。接下来，我们需要用函数参数来表达问题，并查看哪些参数是变化的。在面试中，通常会遇到一两个变化参数，但从技术角度来看，变化参数可以是任意数量。一个经典的单参数问题示例是“确定第 n 个斐波那契数”。一个经典的双参数问题示例是“计算字符串之间的编辑距离”。如果您不熟悉这些问题，不必担心。

确定变化参数数量的一种方法是列出几个子问题的例子并比较这些参数。计算变化参数的数量对于确定我们需要解决的子问题的数量很有帮助，但它本身也有助于我们加强对步骤1中递归关系的理解。

在我们的例子中，每个子问题可能发生变化的两个参数是：

1. 阵列位置 (P)
2. 速度（S）

有人可能会说前面的跑道也在发生变化，但考虑到整个未变化的跑道和位置（P）已经带有该信息，那么这将是多余的。

现在，有了这两个变化的参数和其他静态参数，我们就有了子问题的完整描述。

识别变化的参数并确定子问题的数量。

步骤3：清晰地表达递归关系

这是许多人为了开始编程而匆匆忙忙完成的重要一步。尽可能清晰地表达递归关系可以加深你对问题的理解，并使其他一切都变得更容易。

一旦你弄清楚了递归关系的存在，并用参数来指定问题，这应该是一个自然而然的步骤。问题之间是如何关联的？换句话说，假设你已经计算了子问题。那么，你将如何计算主问题呢？

以下是我们在示例问题中对此的思考：

因为在跳转到下一个位置之前，你可以将速度调整最多 1，所以只有 3 种可能的速度，因此我们可能在 3 个位置进行下一个跳转。

更正式地，如果我们的速度是 S，位置是 P，我们可以从 (S, P) 到：

1. (S, P + S); # 如果我们不改变速度
2. （S - 1，P + S - 1）； # 如果我们把速度改变-1
3. (S + 1, P + S + 1); # 如果我们改变速度 +1

如果我们能找到一种方法，让上述任何一个子问题停止，那么我们也可以从 (S, P) 停止。这是因为我们可以从 (S, P) 过渡到上述三个选项中的任何一个。

这通常意味着对问题的理解已经足够深入（用简单的英语解释），但有时你可能也想用数学的方式表达这种关系。假设我们要计算的函数名为 canStop。然后：

可以停止（S，P）=可以停止（S，P + S）||可以停止（S - 1，P + S - 1）||可以停止（S + 1，P + S + 1）

哇哦，看起来我们找到了递归关系！

递归关系：假设您已经计算了子问题，那么您将如何计算主要问题？

步骤 4：确定基准案例

基准案例是指不依赖于任何其他子问题的子问题。为了找到这样的子问题，你通常需要尝试一些示例，看看你的问题如何简化为更小的子问题，以及在什么情况下无法进一步简化。

问题无法进一步简化的原因是，其中一个参数会变成在问题约束条件下不可能的值。

在我们的示例问题中，我们有两个变化的参数，S 和 P。让我们考虑一下 S 和 P 的哪些可能值可能不合法：

1. P 应该在给定跑道的范围内
2. P 不能使得 runway[P] 为假，因为这意味着我们站在尖刺上
3. S 不能为负数，并且 S==0 表示我们已完成

有时，将我们对参数的断言转换为可编程的基本条件可能有点困难。这是因为，除了列出断言（如果你想让代码看起来简洁，避免检查不必要的条件）之外，你还需要考虑哪些条件是可能的。

在我们的例子中：

1. P < 0 || P >= 跑道长度似乎是正确的做法。另一种选择是考虑将 P == 跑道末端作为基准情况。然而，一个问题可能会分裂成一个超出跑道末端的子问题，所以我们确实需要检查是否存在不等式。

2. 这似乎很明显。我们可以简单地检查runway[P] 是否为假。

3. 与 #1 类似，我们可以简单地检查 S < 0 和 S == 0。然而，这里我们可以推断，S 不可能 < 0，因为 S 最多只会减少 1，所以它必须事先经过 S == 0 的情况。因此，S == 0是 S 参数的充分基准情况。

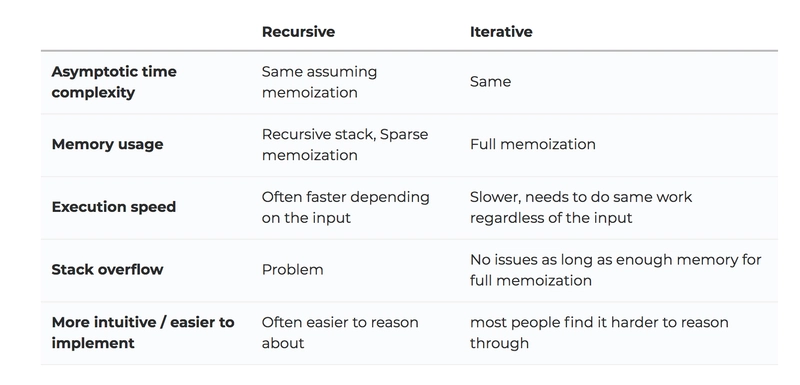
步骤 5：决定是否要以迭代或递归方式实现

到目前为止，我们讨论步骤的方式可能会让你认为我们应该以递归的方式实现这个问题。然而，到目前为止，我们讨论的所有内容都与你决定以递归还是迭代的方式实现这个问题完全无关。在这两种方法中，你都必须确定递归关系和基准条件。

要决定采用迭代还是递归方式，您需要仔细考虑权衡。

堆栈溢出问题通常会导致交易失败，也是你不想在（后端）生产系统中使用递归的原因。但是，就面试而言，只要你提到了权衡利弊，通常两种实现方式都可以接受。你应该对两种实现方式都感到满意。

在我们的具体问题中，我实现了两个版本。以下是 Python 代码：

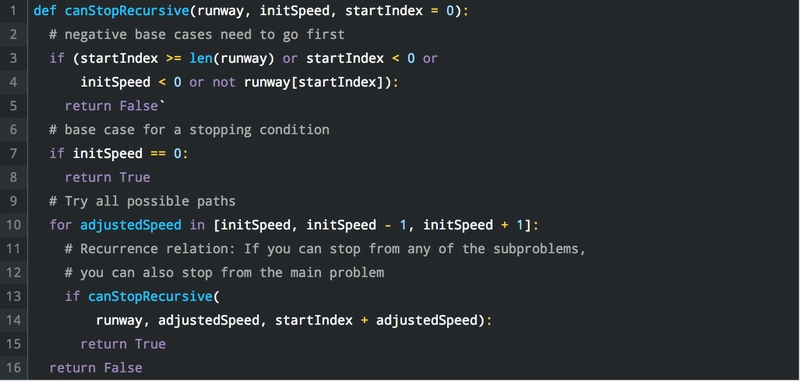
递归解决方案：（原始代码片段可以在这里找到）

迭代解决方案：（原始代码片段可以在这里找到）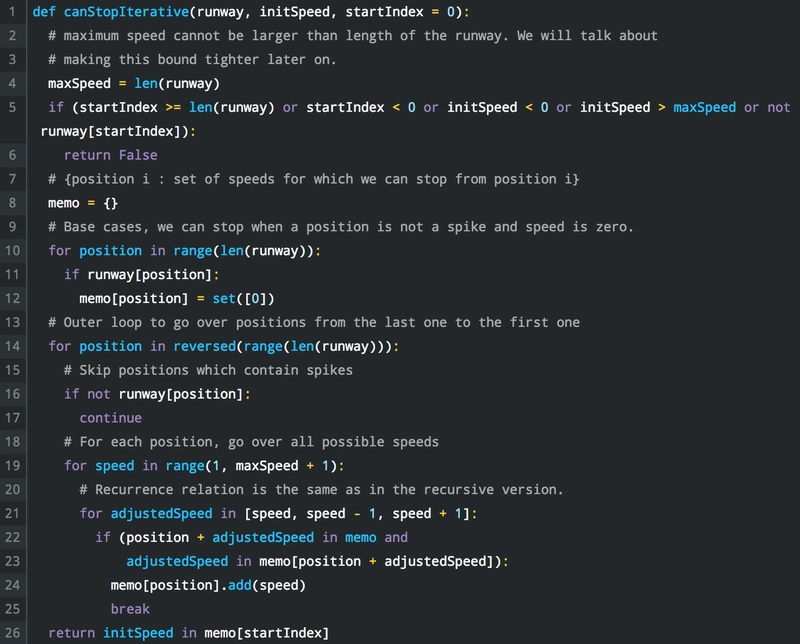

步骤 6：添加记忆

记忆化是一种与动态规划 (DP) 密切相关的技术。它用于存储开销较大的函数调用的结果，并在相同的输入再次出现时返回缓存的结果。为什么要在递归中添加记忆化？因为我们会遇到相同的子问题，如果没有记忆化，它们会被重复计算。这些重复计算通常会导致指数级的时间复杂度。

在递归解决方案中添加 memoization 应该很简单。让我们看看为什么。记住，memoization 只是函数结果的缓存。有时你会为了挤出一些小的优化而偏离这个定义，但将 memoization 视为函数结果缓存是最直观的实现方式。

这意味着您应该：

1. 在每个返回语句之前将函数结果存储到内存中
2. 在开始进行任何其他计算之前，先查找函数结果的内存

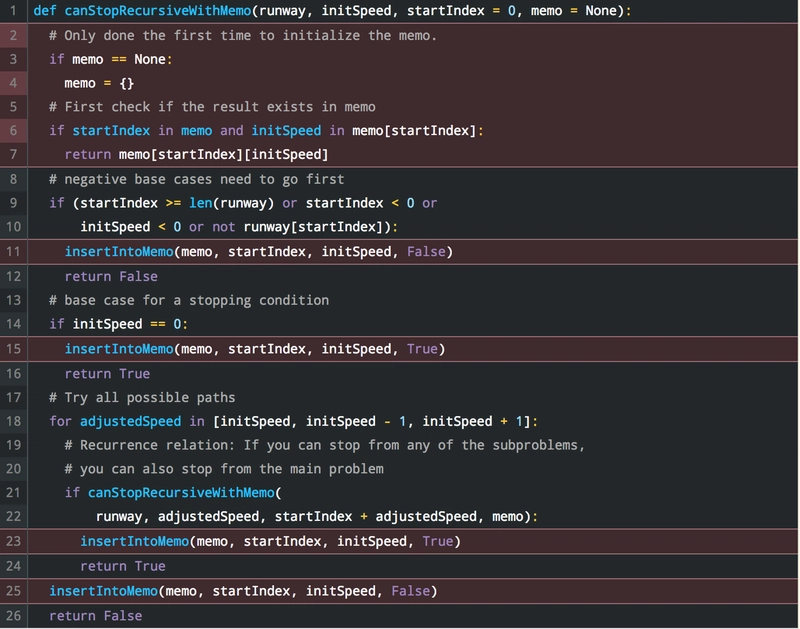
以下是上面添加了记忆的代码（添加的行已突出显示）：

为了说明记忆化和不同方法的有效性，我们来做一些快速测试。我将对目前为止介绍的三种方法进行压力测试。设置如下：

1. 我创建了一条长度为 1000 米的跑道，跑道上随机设置了尖刺（我选择让尖刺出现在任意指定位置的概率为 20%）
2. 初始速度 = 30
3. 我运行了所有函数 10 次并测量了平均执行时间

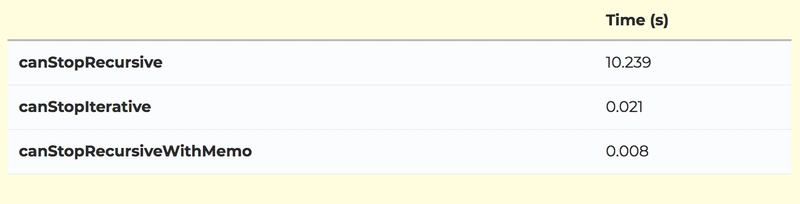
结果如下（以秒为单位）：

您可以看到，纯递归方法比迭代方法多花费大约 500 倍的时间，比带记忆的递归方法多花费大约 1300 倍的时间。请注意，这种差异会随着跑道长度的增加而迅速增大。我鼓励您亲自尝试运行一下。

步骤 7：确定时间复杂度

有一些简单的规则可以大大简化动态规划问题的时间复杂度计算。以下是您需要执行的两个步骤：

1. 计算状态数——这取决于问题中变化参数的数量
2. 想想每个状态所需的工作量。换句话说，如果除了一个状态之外的所有其他状态都已计算，那么计算最后一个状态需要做多少工作量？

在我们的示例问题中，状态数为|P| * |S|，其中

• P 是所有位置的集合（|P| 表示 P 中元素的数量）
• S 是所有速度的集合

在此问题中，每个状态所完成的工作是 O(1)，因为给定所有其他状态，我们只需查看 3 个子问题即可确定结果状态。

正如我们之前在代码中提到的，|S| 受跑道长度 (|P|) 的限制，因此我们可以说状态数为 |P|^2，并且每个状态完成的工作为 O(1)，因此总时间复杂度为 O( |P|^2 )。

然而，似乎 |S| 可以进一步限制，因为如果它真的是 |P|，那么很明显不可能停下来，因为你必须在第一步中跳过整个跑道的长度。

那么，让我们看看如何对 |S| 进行更严格的限制。我们设最大速度为 S。假设我们从位置 0 开始。如果我们试图尽快停下来，并且忽略潜在的峰值，我们能多快停下来？

在第一次迭代中，我们必须至少到达点 (S-1)，将速度从零调整为 -1。从那里开始，我们至少要前进 (S-2) 步，依此类推。

对于长度为 L的跑道，必须满足以下条件：

=> (S-1) + (S-2) + (S-3) + ….+ 1 < L

=> S * (S – 1) / 2 < L

=> S^2 – S – 2L < 0

如果找到上述函数的根，它们将是：

r1 = 1/2 + sqrt(1/4 + 2L) 且 r2 = 1/2 – sqrt(1/4 + 2L)

我们可以将不等式写成：

(S – r1) * (S – r2) < 0

考虑到对于任何 S > 0 和 L > 0，S – r2 > 0，我们需要以下内容：

S – 1/2 – sqrt(1/4 + 2L) < 0

=> S < 1/2 + sqrt(1/4 + 2L)

这是我们在长度为 L 的跑道上可能达到的最大速度。如果速度高于该速度，那么无论尖钉的位置如何，我们都无法从理论上停下来。

这意味着总时间复杂度仅取决于跑道的长度 L，形式如下：

O(L * sqrt(L)) 比 O(L^2) 更好

O(L * sqrt(L)) 是时间复杂度的上限

太棒了，你成功了！🙂

我们讲解的 7 个步骤应该能为你提供一个系统地解决任何动态规划问题的框架。我强烈建议你多练习几个问题，以完善你的方法。

以下是您可以采取的一些后续步骤：

1. 扩展示例问题，尝试找到一条通往停车点的路径。我们解决了一个判断是否可以停车的问题，但如果您还想知道最终在跑道上停车需要采取哪些步骤，该怎么办？您将如何修改现有的实现来实现这一点？

2. 有一件事可能对你巩固对记忆化（memoization）的理解很有帮助，那就是阅读 Python 中的装饰器或其他语言中类似的概念。思考一下它们如何让你为任何想要记忆的函数实现记忆化。

3. 按照我们之前的步骤，做更多动态规划问题。你总能在网上找到很多类似的问题（例如LeetCode或GeeksForGeeks）。练习时，请记住一件事：学习思路，而不是学习问题。思路的数量明显更少，更容易攻克，这对你也有好处。

当您觉得自己已经掌握了这些想法时，请查看Refdash，在那里您将接受高级工程师的面试，并获得有关您的编码、算法和系统设计的详细反馈。