🧠 一个用原生 JS 实现的 AI/神经网络！😱 无需任何库！🤯

你真的尝试过搭建一个神经网络吗？没有，我也没有……直到今天！

在本文中，我们将介绍我学到的一些内容以及用 vanilla JS 编写的一些非常简单的神经网络的 2 个演示。

介绍

我今天早些时候正在阅读@supabase_io的 “AI内容风暴”文章。

我突然明白了。我了解神经网络……但实际上我根本不懂它们！

比如，我了解神经元的概念。但是数学是如何运作的呢？

具体来说，如何使用“反向传播”来训练神经网络？偏差和权重是如何工作的？什么是 S 型函数？等等。

现在，明智的做法是阅读大量文章，找到图书馆并利用它们。

但我不是理智的。

因此，我阅读了大量文章……然后决定建立我的第一个神经网络。

但这还不够难，所以我决定用 JavaScript 来实现（毕竟好像大家都用 Python……）。哦，对了，我还决定不用任何库。哦，我还想用它来做一个可视化工具。

我有点不对劲...我似乎靠痛苦生存。

无论如何，我做到了，以下是我学到的东西。

注意：这不是教程

看，我想说清楚，这不是教程！

这只是我分享在学习和我的第一个神经网络时发现的一些有趣的东西。

请注意，重点放在“首先”，所以请不要将其视为除了有趣的东西之外的任何其他东西，以供观看和玩耍。

我也尽力解释每个部分及其作用，但就像所有事物一样，你对某件事越熟练，解释起来就越好……所以我的一些解释可能有点“不对”！

不管怎样，既然已经解决了这些问题，那就让我们继续吧！

如果您想直接跳到最后的演示，那么请继续！

第一步

好的，首先，我可以构建的最基本的神经网络是什么？

经过一番阅读后，我发现神经网络可以像一些输入神经元和一些输出神经元一样简单。

每个输入神经元都连接到一个输出神经元，然后我们可以为每个连接添加权重。

考虑到这一点，我必须想出一个简单易懂但又足够复杂以确保我的网络正常运行的问题来解决问题。

我决定采用一个神经网络，它获取图表上某个点的 X 和 Y 坐标，然后根据它们是正数还是负数为它们分配一个“团队”（颜色）。

这样我们就有 2 个输入（X 和 Y 位置）和 4 个输出：

1. X > 0 且 Y > 0
2. X < 0 且 Y > 0
3. X > 0 且 Y < 0
4. X < 0 且 Y < 0

由于这里的要求非常简单，我们可以不用一些“隐藏”的神经元（这是我稍后会介绍的内容）并使事情变得非常简单！

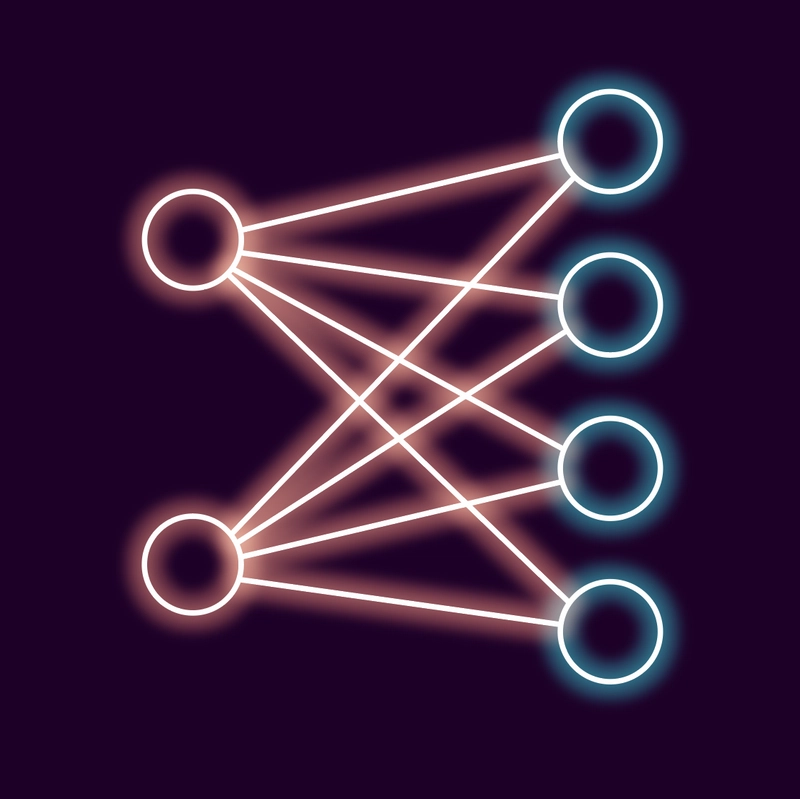
所以本质上我们必须建立一个如下所示的神经网络：

左边的圆圈是我们的输入（X 和 Y 位置），右边的圆圈是我们之前讨论过的输出。

我们的第一个神经元

好的，现在我们可以开始了。

我其实并没有先构建一个神经元。事实上，我先构建了一个可视化工具，因为这是最简单的方法，可以查看它是否正常工作，但我稍后会讲到。

因此，让我们构建一个神经元（或者更具体地说，几个神经元及其连接）。

幸运的是，神经元实际上非常简单！（或者我应该说，它们可以非常简单……在大型语言模型（LLM）等中它们变得更加复杂。）

简单的神经元具有偏差（可以将其想象成内部权重，我们将在最终计算中添加一个数字来加权每个神经元），并且通过每个连接之间的权重连接到其他神经元。

现在回想起来，单独添加每个神经元的连接可能是一个更好的想法，但我决定将每一层神经元和每一层连接作为单独的项目添加，因为这样更容易理解。

因此，构建我的第一个神经网络的代码如下所示：

class NeuralNetwork {
    constructor(inputLen, outputLen) {
        this.inputLen = inputLen;
        this.outputLen = outputLen;
        this.weights = Array.from({ length: this.outputLen }, () =>
            Array.from({ length: this.inputLen }, () => Math.random())
        );
        this.bias = Array(this.outputLen).fill(0);
    }
}

const neuralNetwork = new NeuralNetwork(2, 4);

好的，我跳过了几个步骤，所以让我们简要介绍一下每个部分。

this.inputLen = inputLen;只是this.outputLen = outputLen;为了让我们参考输入和输出的数量。

this.weights = [...]就是连接。现在看起来可能有点吓人，但我们要做的是：

• 创建输出神经元数组（outputLen）
• 为每个数组条目添加一个长度数组inputLen，并用 0 到 1 之间的一些随机值填充它来开始。

该代码的输出示例如下所示：

this.weights = [
  [0.7583747881712366,0.4306037998314902],
  [0.40553698492617807,0.4419651593960727],
  [0.852978801662627,0.9762509253699836],
  [0.8701610553353811,0.5583309725764114]
]

它们主要代表以下内容：

[input 1 to output 1, input 2 to output 1],
[input 1 to output 2, input 2 to output 2],
[input 1 to output 3, input 2 to output 3],
[input 1 to output 4, input 2 to output 4],

那么我们还有this.bias。

这是针对输出层每个神经元的。稍后我们会用它来加到输出值上，使一些神经元更强，一些神经元更弱。

它只是一个由 4 个零组成的数组，因为我们不想要初始偏差！

现在，虽然这是一个神经网络，但它完全没用。

我们无法真正使用它......如果我们使用它，它产生的结果将是完全随机的！

所以我们需要解决这些问题！

使用我们的网络！

我们需要做的第一件事是实际获取一些输入，通过我们的网络运行它们并收集输出。

以下是我的想法：

propagate(inputs) {
  const output = new Array(this.outputLen);
  for (let i = 0; i < this.outputLen; i++) {
    output[i] = 0;
    for (let j = 0; j < this.inputLen; j++) {
      output[i] += this.weights[i][j] * inputs[j];
    }
    output[i] += this.bias[i];
    output[i] = this.sigmoid(output[i]);
  }
  return output;
}

sigmoid(x) {
  return 1 / (1 + Math.exp(-x));
}

这里有两件有趣的事情。

S形函数

首先，一个有趣的事情是我们的sigmoid函数。它的作用是将我们输入的值（比如 12）沿着“S 形”曲线转换为 0 到 1 之间的值。

这是我们将价值观从极端规范化为更统一且始终积极的价值观的方式。

进一步阅读后，我们发现这里还有其他关于如何将值更改为 0 到 1 之间的选项，但我还没有完全探索它们（例如ReLU。

我确信有一些非常好的解释说明为什么需要这样做，但在我的大脑中，这只是将值保持在 0 和 1 之间的方法，以便乘法保持在一定范围内并且值被“平坦化”。

这样，神经元之间就不会出现过于强大的“失控”路径。

例如，假设您有一个权重为 16 的连接和一个权重为 1 的连接，使用我们的 S 型函数，我们可以将差异从 16 倍减少到约 35% 的差异（运行我们的函数后sigmoid(1)为 0.73 和sigmoid(16)0.99）。

这也意味着负值变为正值。

因此，通过我们的 S 型函数运行值意味着负数会转换为 0 到 0.5 之间的值，0 的值正好变为 0.5，大于 0 的值变为 0.5 到 1 之间的值。

如果你仔细想想，这很有意义，因为当我们开始将负数和正数相乘时，我们就可以极大地改变我们的输出。

例如，如果在 100 条路径中有一个负神经元，而其余的都是正神经元，这会将强值变为弱值，并可能导致问题。

无论如何，随着我阅读更多内容并进行更多实验，我相信我会更好地理解这一部分！

我需要偏见吗？

第二个有趣的事情是output[i] += this.bias[i];。

好吧，在这个神经网络中，所有 4 个输出都同样重要，我们没有隐藏的神经元，所以我后来删除了它以简化代码！

然而讽刺的是，在我们更复杂的神经网络中，由于网络反向传播的运作方式，我需要在输出神经元上重新添加偏差。否则，一个输出神经元就会一直处于激活状态。

我无法弄清楚这是否是必要的步骤，或者我的神经网络是否犯了一个错误，而这是为了弥补它。

再次提醒你，我还在学习，只是掌握了基础知识，所以我不知道它是什么！🤣

我们快到了

上面代码的其余部分相当简单。我们只是将每个输入乘以与每个输出相关的权重（并加上不必要的偏差！）。

事实上，我们现在就可以运行它，但结果会很糟糕！让我们解决这个问题！

训练时间到了！

好的，神经网络的最后一个重要部分，训练它！

现在，由于这篇文章很长，我将仅介绍以下训练代码的要点（顺便说一下，我花了将近一个小时来编写...我告诉过你我在这方面是个菜鸟！）

    train(inputs, target) {
        const output = this.propagate(inputs);
        const errors = new Array(this.outputLen);

        for (let i = 0; i < this.outputLen; i++) {
            errors[i] = target[i] - output[i];
            for (let j = 0; j < this.inputLen; j++) {
                this.weights[i][j] +=
                    this.learningRate *
                    errors[i] *
                    output[i] *
                    (1 - output[i]) *
                    inputs[j];
            }
            this.bias[i] += this.learningRate * errors[i];
        }
    }

“为什么花了这么长时间？”我听到你问了！是的，我正在努力弄清楚更新每个权重时需要相乘的所有数据。

也this.learningRate需要一点时间来适应。它只是降低了我们调整权重的速率，这样我们就不会“超过”每个权重的目标值，但将其调整到合理的值需要经验……我没有经验，把它设置得太低了，所以我的代码看起来有问题！

经过一番摆弄之后，我确定了 0.1 这个值（而不是 0.01🤦🏼‍♂️），突然间一切开始变得更好了！

好的，所以我们有一个训练函数。但请记住，这个训练函数只进行一次训练。

我们需要对我们的网络进行多次训练，希望每次训练都能使其更加准确。

我们将在稍后讨论这个问题，但我想分享一下我学到的一个要点/事情。

训练数据调整

我知道我们甚至还没有涵盖最终的训练数据，但这是我学到的一个有趣的观点，它适合这里（因为它解释了为什么我花了这么长时间来编写这个训练函数）。

最初我生成了数百个不同的训练 X 和 Y 坐标，全部都是随机的。

但经过进一步阅读后，我通过仅生成 4 个静态训练点获得了更好的结果：

const trainingData = [
    { x: -0.5, y: -0.5, label: "blue" },
    { x: 0.5, y: -0.5, label: "red" },
    { x: -0.5, y: 0.5, label: "green" },
    { x: 0.5, y: 0.5, label: "purple" }
];

一旦你明白了它就有意义了！

我们希望将价值观“拉”得更接近目标，上述价值观是我们每个区域的确切“中心点”。

因此，对于给定的距离，我们的错误率将始终保持一致。

这意味着我们的神经网络学习得更快，因为我们的错误率会根据距离 X 还是距离 Y 的远近而变大。

我可以解释得更清楚，但这超出了本文的讨论范围。希望如果你仔细思考一下，也能像我一样“豁然开朗”！

具有讽刺意味的是，我回到了更大模型的更随机的数据集，因为我想真正测试我对学习率、过度训练等的理解。

我们有一个功能齐全且有用的神经网络！

事实上，这就是我们的整个神经网络。

但有一件事我们需要做。

我们的训练功能需要运行很多次！

因此，我们需要最后一个函数来实现这一点，它获取我们的训练数据并运行我们的训练函数几百次：

function train() {
  for (let i = 0; i < 10000; i++) {
    const data =
            trainingData[Math.floor(Math.random() * trainingData.length)];
    neuralNetwork.train([data.x, data.y], encode(data.label));
  }
  console.log("Training complete");
}

金发姑娘迭代

请注意，我们在for循环中训练了我们的网络 10,000 次。

10,000 次迭代足以训练这个特定的神经网络。但对于稍后将要介绍的更复杂的模型，我需要更多次迭代（并且降低学习率）。

这是机器学习中一个有趣的部分，你需要对神经网络进行充分的训练（这很难做到正确），但如果训练过度，就会出现“过拟合”，结果反而会变得更糟。所以，为了获得最佳结果，需要达到完美的平衡！

无论如何，这已经很多了，我们终于完成了我们的第一个演示！

简单的 vanilla JS 神经网络演示

它有点乱，但我们的神经网络和所有的训练部分都在下面的 CodePen 的前 67 行中。

剩余的代码行实际上运行我们的网络（neuralNetwork.propagate([x, y]);大约第 85 行），然后将点及其预测的颜色输出到<canvas>.

encode纯粹decode是为了获取我们的输出神经元，找到哪个神经元具有最高的激活度，然后将其映射到颜色以供我们可视化。

最后要理解的是，我们的输出神经元都会有一个值。神经网络的输出不仅仅是 1、0、0、0。

相反，它会为每个输出神经元输出一个“确定性”或猜测值。所以我们会得到类似0.92,0.76, 0.55, 0.87这样的输出。

这就是为什么我们有这个decode函数，它找到输出最高的神经元并将其作为我们的最终猜测！

// this line finds the max value of all of our output neurons and then returns its index so we can use that to classify our X and Y coordinates.
const maxIndex = output.indexOf(Math.max(...output));

使用方法及实际演示

使用该示例，您有 3 个按钮：

• 训练——对我们的神经网络进行训练，因为它开始时是未经训练和随机的。
• 点分类- 用于运行我们的神经网络。它会在图形上绘制点并为其分配颜色。我建议在训练前后都运行这个步骤。
• 重置- 这将创建一个新的未经训练的神经网络。非常适合测试训练前后点的分类效果。

还要注意，每个区域都根据其应显示的颜色进行了着色。这确实能让你看到一个随机且未经训练的神经网络距离成功还有多远（重置后再对要测试的点进行分类）！

玩一玩吧！

我们最基本的神经网络结束了

所以我们有最基本的神经网络！

它很好地满足了我们的需求，并且我们设法学习了一些关于反向传播（我们train在主类中的功能）以及权重和偏差的知识。

但这非常有限。如果我们将来想做更高级的事情，就需要添加一些隐藏神经元！

版本 2 - 隐藏神经元

好的，那么为什么要有隐藏神经元呢？它们有什么用途？

在更复杂的例子中，它们可以作为获取输入并为其分类方式添加更多维度的一种方式。

我们仍然使用 2 个输入神经元和 4 个输出神经元，但这次我们在中间添加了一个额外的层（我们可以更改和调整其中的神经元数量）。

所以我们的神经网络看起来像这样：

由于神经网络需要处理更多的输入并进行更复杂的计算，隐藏层中的额外神经元可以使它们更好地对输入进行分类并提供更好的结果。

隐藏层也可以有不同的“深度”。

假设我们有 2 个输入神经元。我们可以将它们连接到 6 个“隐藏”神经元，然后将它们连接到我们的 4 个输出神经元。

但我们也可以将第一层的 6 个神经元连接到第二层的隐藏神经元。第二层可以有 8 个神经元，然后连接到我们的 4 个输出神经元。

但接下来还有很多内容，而且这只是为了学习基础知识，所以我选择添加一个隐藏层。这也意味着我可以将每个连接层保留为一个单独的数组，这在现阶段更容易理解！

那么有什么新鲜事吗？

没有太大的变化，只是我们有更多的连接和更多的神经元！

您可以将其视为将我们原来的两个神经网络串联起来，只是第一个神经网络的输出现在充当第二个神经网络的输入。

虽然代码可能更加复杂，但我们的神经网络遵循相同的原理。

以下是代码：

class NeuralNetwork {
  constructor(inputSize, hiddenSize, outputSize) {
    this.inputSize = inputSize;
    this.hiddenSize = hiddenSize;
    this.outputSize = outputSize;
    this.weightsInputToHidden = Array.from({ length: hiddenSize }, () =>
            Array.from({ length: inputSize }, () => Math.random() * 2 - 1)
        );
    this.biasHidden = Array(hiddenSize).fill(0);
    this.weightsHiddenToOutput = Array.from({ length: outputSize }, () =>
      Array.from({ length: hiddenSize }, () => Math.random() * 2 - 1)
    );
    this.biasOutput = Array(outputSize).fill(0);
    this.learningRate = document.querySelector('#learningRate').value; // Adjusted learning rate
    this.hiddenLayer = new Array(this.hiddenSize);
  }

  feedForward(inputs) {
    for (let i = 0; i < this.hiddenSize; i++) {
      this.hiddenLayer[i] = 0;
      for (let j = 0; j < this.inputSize; j++) {
        this.hiddenLayer[i] +=
        this.weightsInputToHidden[i][j] * inputs[j];
      }
      this.hiddenLayer[i] += this.biasHidden[i];
      this.hiddenLayer[i] = sigmoid(this.hiddenLayer[i]);
    }

    const output = new Array(this.outputSize);
    for (let i = 0; i < this.outputSize; i++) {
      output[i] = 0;
      for (let j = 0; j < this.hiddenSize; j++) {
        output[i] +=
        this.weightsHiddenToOutput[i][j] * this.hiddenLayer[j];
      }
      output[i] += this.biasOutput[i];
      output[i] = sigmoid(output[i]);
    }
    return output;
  }

  train(inputs, target) {
    for (let i = 0; i < this.hiddenSize; i++) {
      this.hiddenLayer[i] = 0;
      for (let j = 0; j < this.inputSize; j++) {
        this.hiddenLayer[i] +=
        this.weightsInputToHidden[i][j] * inputs[j];
      }
      this.hiddenLayer[i] += this.biasHidden[i];
      this.hiddenLayer[i] = sigmoid(this.hiddenLayer[i]);
    }

    const output = new Array(this.outputSize);
    for (let i = 0; i < this.outputSize; i++) {
      output[i] = 0;
      for (let j = 0; j < this.hiddenSize; j++) {
        output[i] += this.weightsHiddenToOutput[i][j] * this.hiddenLayer[j];
      }
      output[i] += this.biasOutput[i];
      output[i] = sigmoid(output[i]);
    }

    const errorsOutput = new Array(this.outputSize);
    const errorsHidden = new Array(this.hiddenSize);

    for (let i = 0; i < this.outputSize; i++) {
      errorsOutput[i] = target[i] - output[i];
      for (let j = 0; j < this.hiddenSize; j++) {
        this.weightsHiddenToOutput[i][j] +=
          this.learningRate *
          errorsOutput[i] *
          output[i] *
          (1 - output[i]) *
          this.hiddenLayer[j];
        }
        this.biasOutput[i] += this.learningRate * errorsOutput[i];
      }

      for (let i = 0; i < this.hiddenSize; i++) {
        errorsHidden[i] = 0;
        for (let j = 0; j < this.outputSize; j++) {
          errorsHidden[i] += this.weightsHiddenToOutput[j][i] * errorsOutput[j];
        }
        this.biasHidden[i] += this.learningRate * errorsHidden[i];
        for (let j = 0; j < this.inputSize; j++) {
          this.weightsInputToHidden[i][j] +=
          this.learningRate *
          errorsHidden[i] *
          this.hiddenLayer[i] *
          (1 - this.hiddenLayer[i]) *
          inputs[j];
        }
      }
   }
}

现在，不要被吓倒，我只是复制了几个循环，其中目标数据集略有不同，需要进行操作。

我们添加了一组额外的偏差（针对我们的隐藏层）和一组额外的连接：我们的输入层到我们的隐藏层，然后我们的隐藏层现在连接到我们的输出层。

最后，我们的train函数有几个额外的循环，只是为了反向传播每个步骤。

唯一值得一提的变化是，我们现在有了第三个输入参数（在中间），表示隐藏神经元的数量。

虽然丑，但似乎有效

看，我想再说一次，这是我边学边做的，所以代码反映了这一点。

这里有很多重复，并且扩展性不强。

然而，据我所知，它是有效的。

话虽如此，尽管它有效，但它的表现似乎比我们原来的、简单得多的神经网络要差。

这要么意味着我犯了一个错误（很可能），要么是我没有“拨入”正确的训练设置。

说到这个...

添加一些变量来玩

由于这比较复杂，我在一些快速设置中“做了修改”。

现在我们可以更新：

• 训练数据大小——我们生成的不同随机点的数量
• 训练迭代train——我们从训练集中选择随机数据点并将其输入到神经网络函数中的次数。
• 学习率——我们根据错误调整速度的乘数。
• 隐藏节点（超过 2 个！） - 调整第二层中隐藏节点的数量（需要您再次初始化网络，否则它将中断！）
• 要分类的点- 传递给我们训练的神经网络并绘制在图表上的点的数量。

这意味着我们可以更快地处理值，看看它们对我们的神经网络及其准确性有何影响！

最后一件事

哦，我添加了一个按钮来直观地显示神经网络的样子。

一定要点击“可视化神经元和权重”，但它还没完成。我目前也不打算完成它，因为我想彻底重新设计我构建神经网络的方法，使其更具可扩展性。

不过，按钮就在那里，随便按吧。更好的是，能帮我修一下就好了！🤣💗

演示

控制与以前相同，加上前两个小节中提到的输入。

玩一玩，看看你是否可以微调学习率、神经元数量和训练设置以获得真正准确的结果！

确保更新一些值，重新初始化神经网络，尝试不同数量的隐藏神经元等。

如果您和我一样是初学者，希望您能够开始了解一些事情！

结论

使用 vanilla JS 构建神经网络真的很有趣。

我没见过很多人这样做，所以我希望它对你或至少对某些人有用！

我学到了很多关于偏见、反向传播（神经网络的关键）等方面的知识。

显然，这个例子和从中学到的东西只占机器学习的 1%。但对于像我这样的微型、未优化的神经网络，以及拥有数十亿参数的庞大模型，其核心原理是相同的。

这个例子就像是机器学习（ML）和神经网络的“hello world”。

接下来，我非常想尝试构建一个更大、结构更合理、更易于扩展的神经网络，看看能否实现光学字符识别 (OCR)。你可以把它看作是机器学习和神经网络的“待办事项清单”！

发表评论。

你是神经网络专家吗？告诉我我哪里出错了！

你和我一样是个彻头彻尾的新手吗？那就告诉我，这是否帮助你理解了，哪怕只是一点点！或者，这是否反而让你更困惑了！😱

最重要的是，如果这篇文章激发了你对我糟糕的编码感到苦笑，或者想要构建自己的神经网络……那么我很高兴它对你产生了一些影响，并且无论如何都很乐意听到你的反馈！💗