图论简介

如果没有需要解决的问题，世界上很多事物都不会存在。这个道理适用于一切事物，但在计算机科学的世界里，这一点尤为明显。

有人需要一种方法来追踪事物的顺序，于是他们尝试并创建了不同的数据结构，直到找到最适合他们试图解决的特定问题的数据结构。还有人需要一种存储数据的好方法，于是他们尝试了不同的数字系统，直到找到一种最适合他们想要包含的信息类型的数字系统。人们需要一种标记和处理任务的好方法，于是他们找到了一种基于现有工具的方法，并创建了一种方法，能够在任何特定时间处理一个系统需要处理的所有任务。

当然，计算机科学并不是唯一一个在前人的基础上进行创新和发展的领域，但我认为它在某种程度上是独一无二的：计算机科学的创新依赖于并建立在其自身的抽象之上。

我在这个系列中多次讨论抽象，因为最终，这才是这个系列的主题：在我们日常使用的事物背后，发现抽象的乐趣。而且，当我说“我们”时，我指的只是我们作为程序员，技术的创造者——也包括我们作为用户，技术的消费者。

那么，接下来我们要学习哪个令人惊叹的抽象概念呢？既然我们已经是树形数据结构的专家了，那么了解树的起源似乎再合适不过了。树实际上是你可能已经听说过的一个概念的子集：图。但为了真正理解我们为什么使用图以及图是什么，我们需要深入探究一个源自离散数学的理论的根源：图论。

如果这是你第一次接触离散数学，别担心——这也是我的第一次！让我们一起努力——尽量在这个过程中保持理智。

松散的图表

当我们初次研究非线性结构时，我们了解到它们最基本的特征：它们的数据不遵循一定的顺序——至少，不像我们在数组或链表中看到的那样，遵循明显的数值顺序。正如我们所了解的，树从根节点开始，并且可能连接到其他节点，这意味着树中可能包含子树。树由一组特定的规则定义：一个根节点可能连接到其他节点，也可能不连接到其他节点，但最终，所有子树都源于一个特定位置。有些树甚至有更具体的规则，例如二叉搜索树，它在任意给定时刻只能有两个指向两个节点的链接。

但如果我们做点疯狂的事，把这些规则抛到九霄云外呢？嗯，事实证明，我们完全可以做到！只不过我们不再需要处理树了——我们需要处理的是一个叫做图的东西。

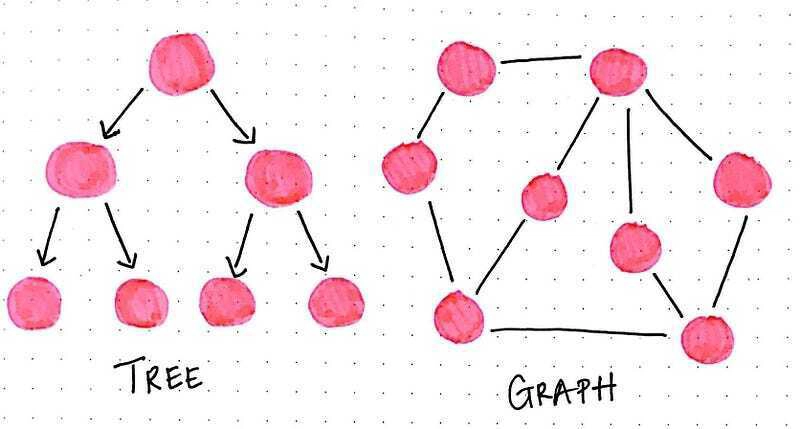
树只不过是图的受限类型，只是需要遵循更多规则。树永远是图，但并非所有图都是树。

那么，是什么使得树与大图伞有所不同呢？

首先，树只能单向流动，从根节点到叶节点或子节点。树也只能有单向连接——一个子节点只能有一个父节点，并且树不能有任何环路或循环链接。

有了图，所有这些限制就都消失了。图没有“根”节点的概念。为什么会有根节点呢？实际上，节点可以以任何可能的方式连接。一个节点可能连接到另外五个节点！图也没有“单向”流动的概念——相反，它们可能有方向，也可能根本没有方向。或者，更复杂的是，它们可能有一些链接有方向，而另一些链接没有方向！但我们今天不讨论这个。

让我们先从简单的事情开始。

有方向的图和无方向的图

好吧，我们知道图几乎打破了我们已知的所有规则。然而，每个图都必须具备一个特征：每个图至少需要一个节点。正如树至少需要一个根节点才能被视为“树”一样，图也至少需要一个节点才能被视为“图”。只有一个节点的图通常被称为单例图，尽管我们实际上不会讨论它。

我们将要处理的大多数图表都比较复杂。不过，别担心——我们今天不会深入研究那些超级复杂的图表。相信我，有些图表真的很复杂！

相反，让我们看一下两种很容易发现并且在图论问题中很常见的图类型：有向图和无向图。

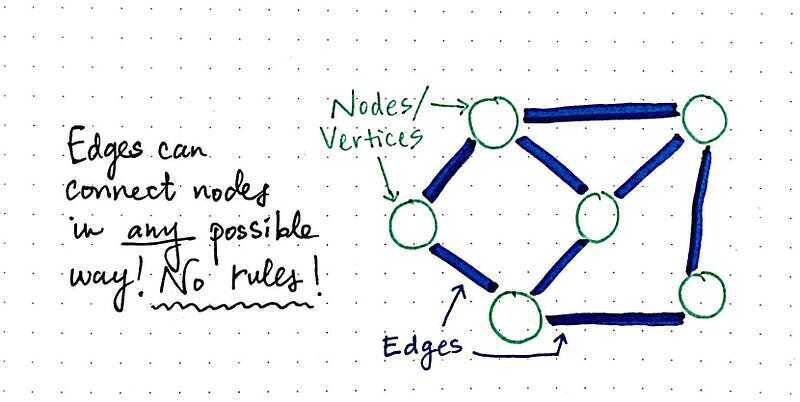
我们知道，图中一个节点与另一个节点的连接方式并没有固定的规则。边（有时也称为链接）可以以任何可能的方式连接节点。

在识别和定义图时，不同类型的边非常重要。事实上，这是图与图之间最大、最明显的区别之一：边的类型。大多数情况下（除了一个例外，我们今天不会讨论），图可以包含两种类型的边：有方向或流向的边，以及无方向或流向的边。我们分别称之为有向边和无向边。

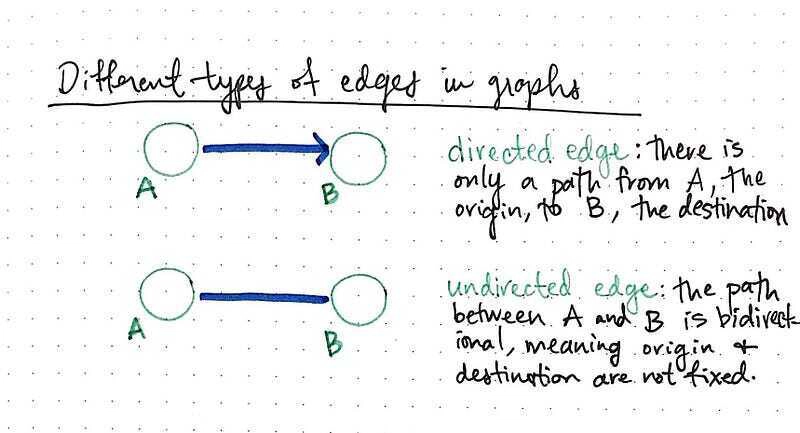
在有向边中，两个节点以一种非常特殊的方式连接。在下面的例子中，节点 A 连接到节点 B；这两个节点之间只有一种路径——只有一个方向。我们通常将出发的节点称为 原点，将要前往的节点称为目的地。在有向边中，我们只能 从 原点 前往 目的地，而不能反过来。

然而，对于无向边来说，情况就完全不同了。在无向边中，我们可以行进的路径是双向的。也就是说，两个节点之间的路径是双向的，这意味着起点和终点节点并不固定。

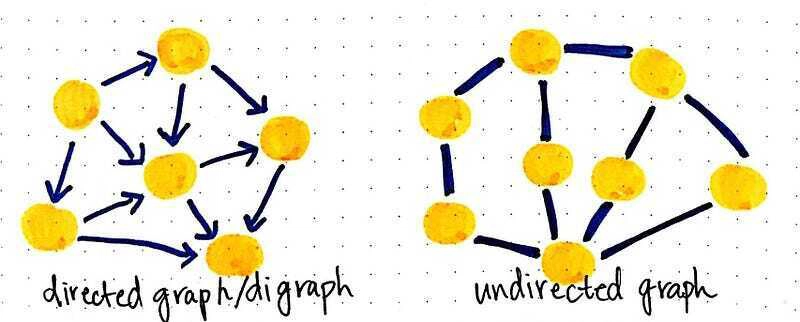
这种区分实际上非常重要，因为图中的边决定了图的名称。如果图中的所有边都是有向的，则该图被称为有向图，也称为有向图。如果图中的所有边都是无向的，则该图被称为————你猜对了————无向图！想想看，对吧？

这一切都很酷，但目前我想知道两件事——所有这些图表究竟从何而来？以及……我们为什么要关心它们？

让我们调查一下。

谨慎行事：我们现在处于图表领域

计算机科学喜欢借鉴。更具体地说，它借鉴了很多逻辑和数学的概念。事实证明，图就是这种情况。

我们所知的计算机科学图形数据结构实际上来自数学和图形的研究，即图论。

在数学中，图形是一种正式表示网络的方式，网络基本上只是相互连接的对象的集合。

事实证明，当计算机科学家将图论应用于代码（并最终将图实现为数据结构）时，他们并没有做出太多改变。因此，我们用来描述和实现图的许多术语，正是我们在图论的数学参考文献中看到的术语。

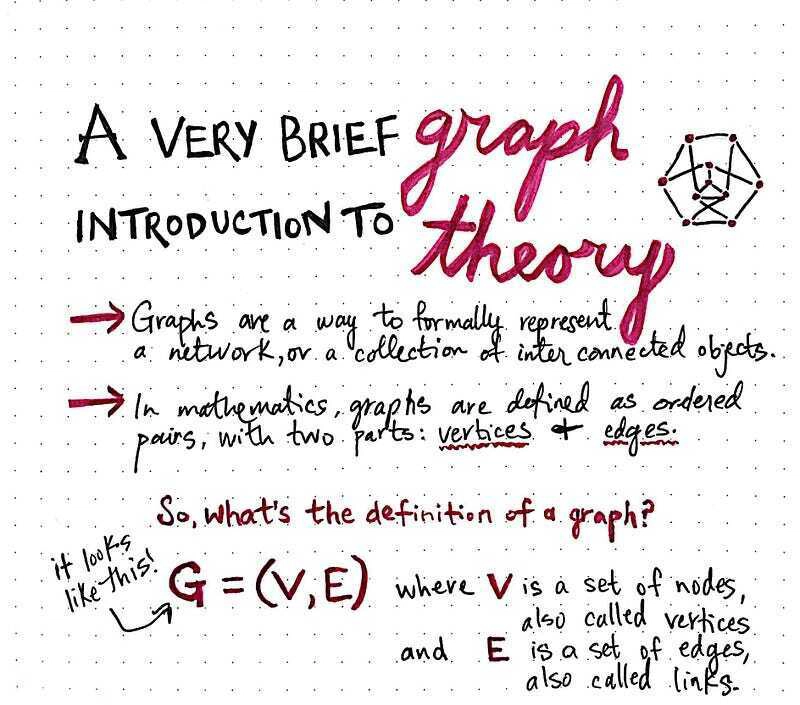
例如，用数学术语来说，我们将图描述为有序对。还记得高中代数中我们学过的(x,y)有序对坐标吗？这里的情况类似，但有一点不同：图的组成部分不是x和y ，而是： v表示顶点，e表示边。

图的正式数学定义就是：G = (V, E)。就是这样！真的。我保证。

但是等一下——如果我们的图有多个节点和多条边怎么办？事实上……如果它有多个节点，它几乎总是有多条边。这个定义到底是怎么回事？

嗯，它之所以有效是因为有序对—— （V，E） ——实际上是由两个 对象组成的：一组顶点和一组边。

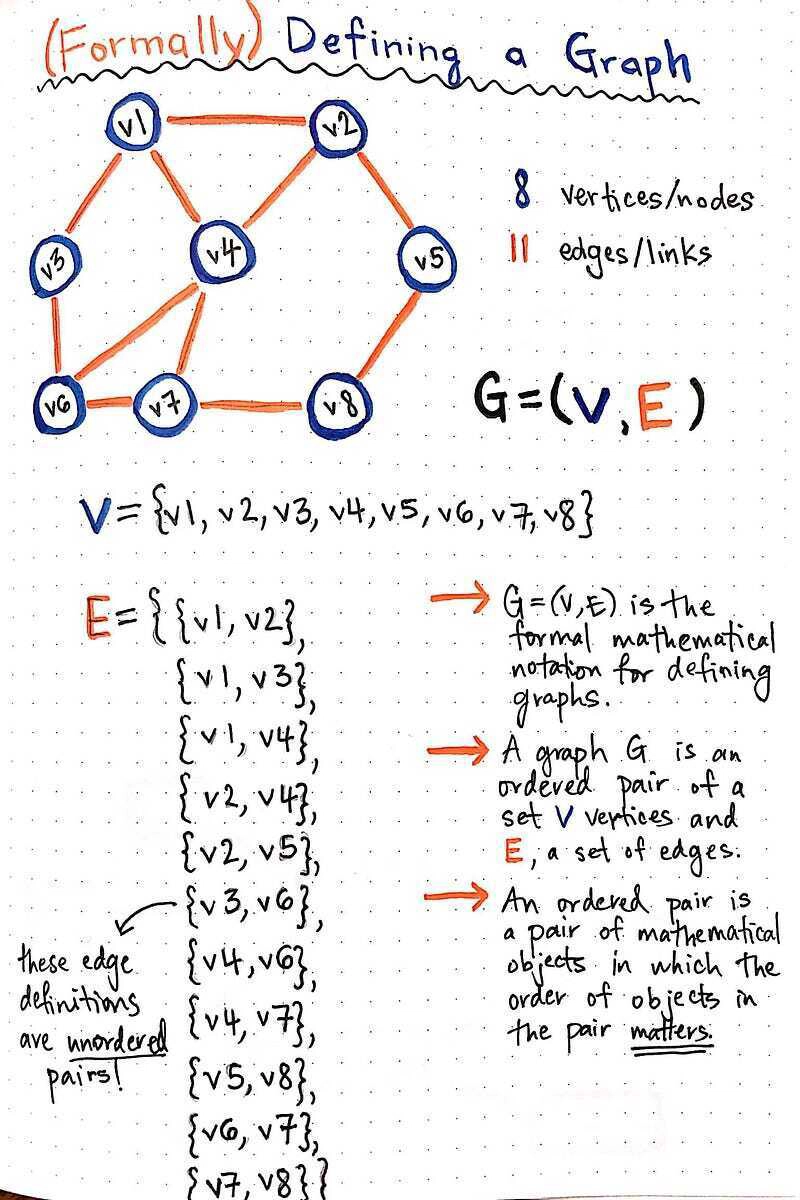
好的，现在我明白了。但如果我举个例子，把图的定义写出来，会更清楚！所以我们就照着做吧。下面的例子中，我们有一个无向图，有 8 个顶点和 11 条边。

那么这里发生了什么？

好吧，我们写出了有序对(V, E) ，但由于其中每个元素都是一个对象，所以我们也必须把它们写出来。我们将V定义为对 8 个顶点的无序引用集合。“无序”在这里非常重要，因为记住，与树不同，它没有节点的层级结构！这意味着我们不需要对它们进行排序，因为顺序在这里并不重要。

我们还必须将E定义为一个对象，其中包含一堆边对象。再次注意，我们的边对象也是无序的。为什么会这样？嗯，这是什么类型的图？有方向或流向吗？有固定的“起点”和“终点”吗？

不，没有！这是一个无向图，这意味着边是双向的，并且起始节点和目标节点不是固定的。所以，我们的每个边对象也是无序对。

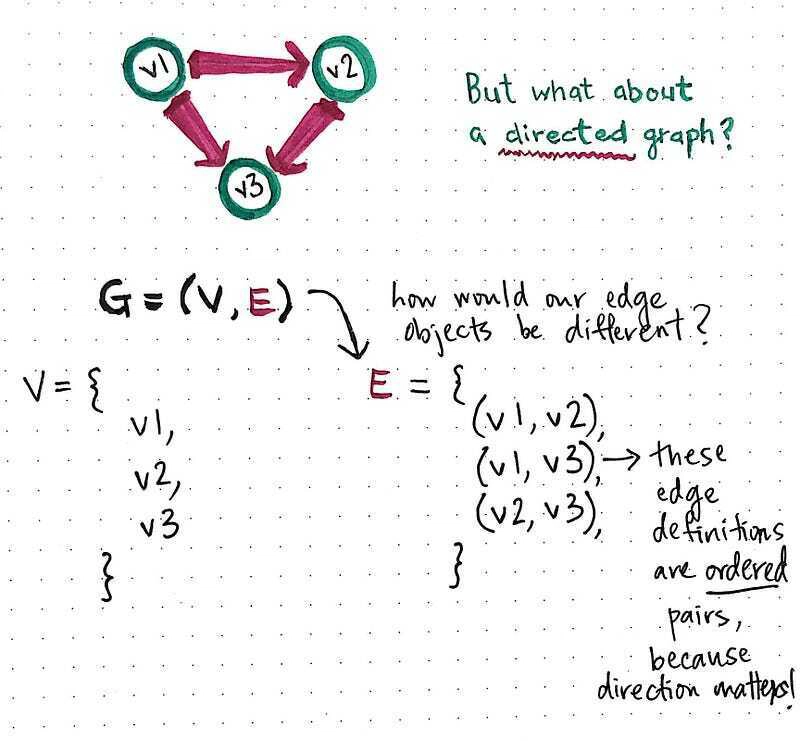
当然，这种特殊性不禁让我们思考：如果这是一个有向图会怎样？是时候再举一个例子了！这是一个有向图，有三个顶点和三条边：

我们在这里定义顶点的方式看起来没什么不同，但让我们更仔细地看看边的定义。在这种情况下，我们的边对象是有序对，因为方向实际上很重要！由于我们只能从起始节点到目标节点，所以我们的边必须是有序的，这样起始节点就是我们每条边定义中两个节点中的第一个。

太棒了，这就是我们对图的定义。但是……我们什么时候才能真正用到图呢？嗯，你今天可能用过一个。只是你可能还没意识到而已！是时候改变一下了。

超级社交图谱

图表在我们周围随处可见，只是我们并不总是能看清它们的本质。

事实上，阅读这篇文章本身，你现在就仿佛置身于一张图之中。网络就是一个巨大的图结构！当我们在网站之间点击，并在 URL 之间来回切换时，我们实际上就是在一张图中导航。有时，这些图中的节点的边是无向的——我可以从一个网页切换到另一个网页——而其他节点的边是有向的——我只能从网页 A 切换到网页 B，而不能反过来。

但还有一个更好的例子可以完美地说明我们日常与图表的互动：社交网络。

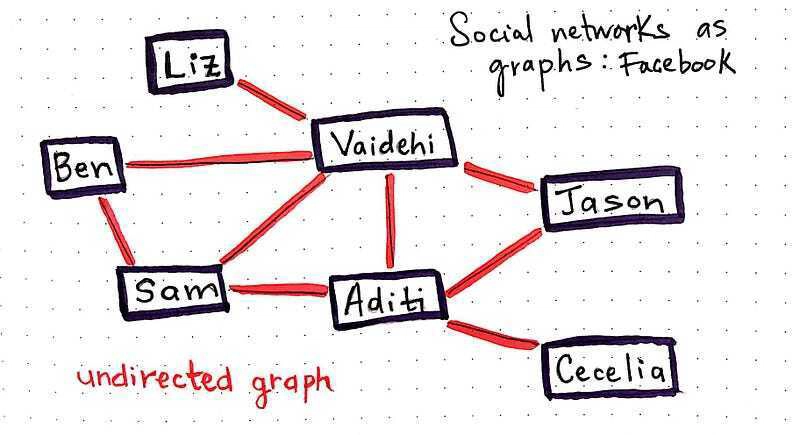
Facebook，一个庞大的社交网络，本身就是一种图谱。如果我们深入思考它的实际运作，就能更好地理解如何定义它，以及它究竟是一种什么样的图谱。在 Facebook 上，如果我加你为好友，你必须接受我的请求。如果你不先成为我的好友，我就不可能在网络上成为你的好友。两个用户（用图的术语来说，就是节点或顶点！）之间的关系是双向的。没有“起点”和“终点”节点的概念——相反，你是我的好友，我也是你的好友。

你能猜出 Facebook 是以什么类型的图表实现的吗？

如果你猜的是无向图，那你猜对了！干得好。关系是双向的，所以如果我们把 Facebook 的好友网络定义为一个图，那么当我们把它们写出来时，它的边最终都会变成无序对。

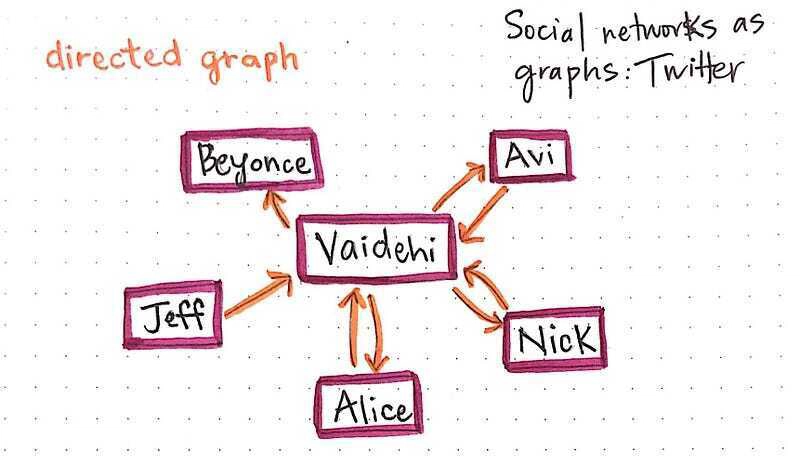
另一方面，Twitter 的运作方式与 Facebook 截然不同。我可以关注你，但你可能不会关注我。举个例子：我关注了碧昂斯，但她肯定不会关注我（真遗憾）。

我们可以将 Twitter 表示为一个有向图。我们创建的每条边代表一种单向关系。当你在 Twitter 上关注我时，你就会在图中创建一条边，以你的账户为起点，以我的账户为终点。

那么，当我回粉你时会发生什么？我会改变你关注我时创建的边吗？它会突然变成双向的吗？嗯，不会，因为我可以随时取消关注你。当我在 Twitter 上回粉你时，我会创建第二条边，以我的账户为起点，以你的账户为终点。

同样的模型也适用于 dev.to，它允许你关注和取消关注作者！事实上，这种网络模型无处不在。一旦我们抽象出所有层级，它就变成了一个图。真的，它是多么强大的东西啊。

资源

关于图的书籍已经写了很多了。我这里涵盖的信息当然不足以写成一本书，但这并不意味着你不能继续学习图！从下面的精彩链接开始，用更多图论的精彩内容充实你的大脑吧。

1. 树和图之间的区别，Poonam Dhanvani
2. 数据结构树和图有什么区别？，StackOverflow
3. 图论在计算机科学中的应用：概述，SGShirinivas 等人。
4. 图遍历，Jonathan Cohen 教授
5. 数据结构：图表简介，mycodeschool