你必须知道的 7 个 JavaScript 数据结构

作者：Ryan Thelin 和 Amanda Fawcett

在解决编码问题时，效率至关重要——从编码时间到运行时间，再到用于解决方案的内存量。值得庆幸的是，JavaScript 开发人员使用了许多预先设定的数据结构，旨在解决常见需求和实际问题。对数据结构的掌握是区分新手开发人员和经验丰富的老手的关键因素。

也许你刚刚开始接触数据结构，又或者你已经编程多年，只是需要复习一下。今天，我们将带你了解 JS 开发者必备的 7 大数据结构。

以下是我们今天要讨论的内容

• 什么是数据结构
• 七大 JS 数据结构
• 数据结构面试题
• 资源

让我们开始吧

什么是数据结构

从高层次上讲，数据结构是一种存储和组织数据的技术，使其更易于修改、导航和访问。数据结构决定了数据的收集方式、访问数据的功能以及数据之间的关系。数据结构几乎应用于计算机科学和编程的所有领域，从操作系统到基本的原生代码，再到人工智能。

数据结构使我们能够：

• 管理和利用大型数据集
• 从数据库中搜索特定数据
• 设计针对特定程序的算法
• 一次处理来自用户的多个请求
• 简化并加速数据处理

数据结构对于高效解决实际问题至关重要。毕竟，我们组织数据的方式对性能和可用性影响巨大。事实上，大多数顶级公司都要求应聘者对数据结构有深入的理解。这些技能表明你知道如何有效地管理数据。任何想要通过编程面试的人都需要掌握数据结构。

JavaScript 具有原始和非原始数据结构。原始数据结构和数据类型是编程语言固有的，包括布尔值、空值、数字、字符串等。非原始数据结构不是由编程语言定义的，而是由程序员定义的，包括线性数据结构、静态数据结构和动态数据结构，例如队列和链表。

现在您已经了解了数据结构为何如此重要，让我们来讨论一下每个 JavaScript 开发人员需要了解的 7 种最重要的数据结构。

你需要了解的 7 个 JavaScript 数据结构

大批

数组是所有数据结构中最基本的一种，它将数据存储在内存中以供后续使用。每个数组的单元格数量在创建时就已确定，并且每个单元格都有一个对应的数字索引，用于选择其数据。无论何时使用数组，只需提供所需的索引，即可访问其中的任何数据。

优势

• 创建和使用简单。
• 复杂数据结构的基础构建块

缺点

• 固定大小
• 插入/删除或重新排序值的成本很高
• 排序效率低

应用

• 基本电子表格
• 在诸如哈希表之类的复杂结构中

如需更深入的解释，请参阅我们关于数组的 Edpresso 文章！

队列

队列在概念上与堆栈类似；两者都是顺序结构，但队列按照元素的输入顺序而不是最新元素进行处理。因此，队列可以被认为是堆栈的 FIFO（先进先出）版本。它们可以用作请求的缓冲区，按接收顺序存储每个请求，直到可以处理为止。

想象一下单车道隧道：第一个进入的车辆也第一个离开。如果其他车辆想离开，但第一个车辆停了下来，那么所有车辆都必须等到第一个车辆离开后才能继续行驶。

优势

• 动态尺寸
• 按收到的顺序排列订单数据
• 运行时间短

缺点

• 只能检索最旧的元素

应用

• 在接收频繁数据时可作为缓冲区
• 方便地存储订单敏感数据（例如存储的语音邮件）
• 确保最旧的数据首先被处理

链表

链表是一种数据结构，与前三种结构不同，它不使用数据在内存中的物理位置。这意味着，链表使用引用系统而不是索引或位置：元素存储在包含指向下一个节点的指针的节点中，如此循环往复，直到所有节点都链接起来。该系统允许高效地插入和删除元素，而无需重新组织数据。

优势

• 高效插入和删除新元素
• 比重组数组更简单

缺点

• 比数组占用更多内存
• 检索特定元素效率低下
• 向后遍历列表效率低下

应用

• 最适合用于必须从未知位置快速连续地添加和删除数据的情况

如需更深入的解释，请参阅我们关于链接列表的 Edpresso 文章！

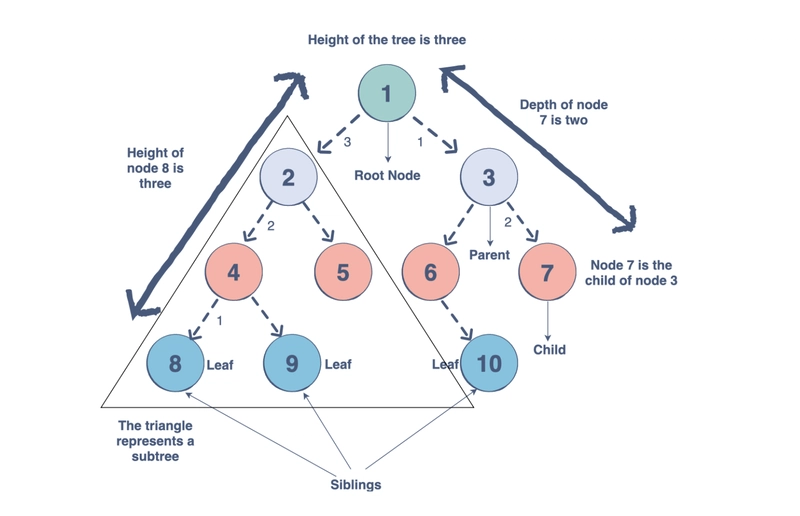
树木

树是另一种基于关系的数据结构，专门用于表示层次结构。与链表类似，节点既包含数据元素，也包含标记其与直接节点关系的指针。

每棵树都有一个“根”节点，所有其他节点都从该节点分支出来。根节点包含对其下方所有元素的引用，这些元素被称为“子节点”。如此循环往复，每个子节点都会分支出更多子节点。

带有链接子节点的节点称为内部节点，而没有子节点的节点称为外部节点。一种常见的树类型是“二叉搜索树”，它用于轻松搜索存储的数据。这些搜索操作非常高效，因为其搜索时间不取决于节点数量，而是取决于树的层数。

这种类型的树由四条严格的规则定义：

1. 左子树仅包含元素小于根的节点。
2. 右子树仅包含元素大于根的节点。
3. 左子树和右子树也必须是二叉搜索树。它们必须遵循上述规则，并且其树的“根”也必须遵循上述规则。
4. 不能有重复的节点，即没有两个节点可以具有相同的值。

优势

• 非常适合存储层次关系
• 动态尺寸
• 快速插入和删除操作
• 在二叉搜索树中，插入的节点会立即排序。
• 二叉搜索树的搜索效率很高；长度仅为 O（高度）。

缺点

• 重新排列节点速度慢
• 子节点不保存有关其父节点的信息
• 二叉搜索树不如更复杂的哈希表快
• 如果不使用平衡子树实现，二叉搜索树可能会退化为线性搜索（扫描所有元素）。

应用

• 存储分层数据，例如文件位置。
• 二叉搜索树非常适合需要搜索或排序数据的任务。

如需更深入的解释，请参阅我们关于树木的 Edpresso 文章！

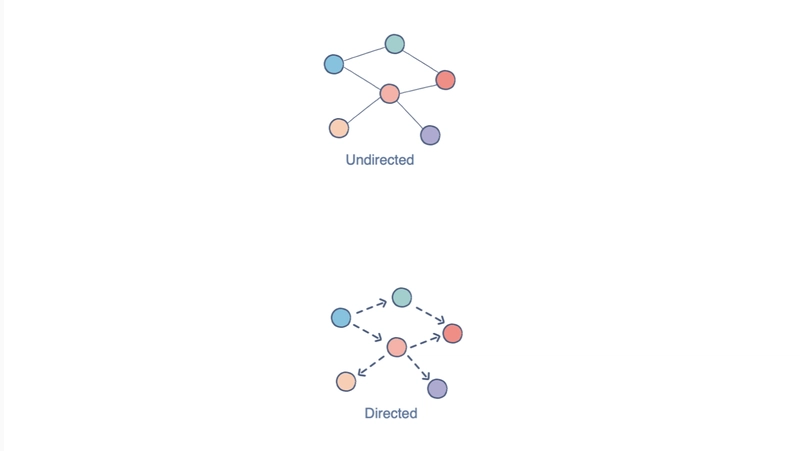
图表

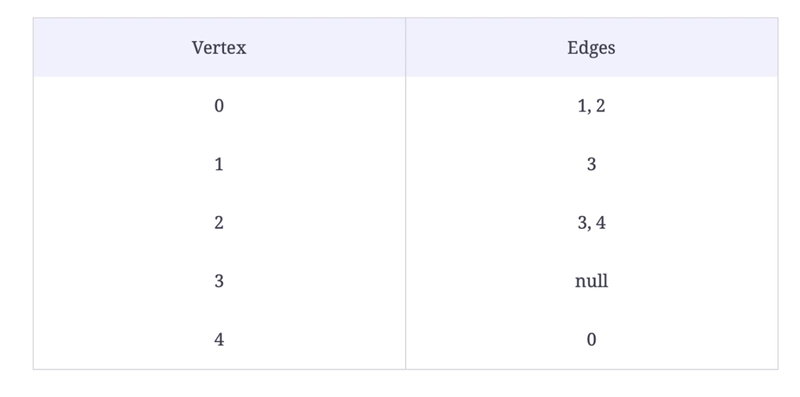
图是一种基于关系的数据结构，有助于存储类似网络的关系。每个节点（在图中称为顶点）都有一个标题（A、B、C 等）、一个包含的值，以及与其他顶点之间的链接列表（称为边）。

在上面的例子中，每个圆都是一个顶点，每条线都是一条边。如果以书面形式表达，这个结构看起来应该是这样的：

V = {a, b, c, d}

E = {ab, ac, bc, cd}

虽然一开始很难想象，但这种结构在以文本形式传达关系图（从电路到火车网络）方面非常有价值。

优势

• 可以通过文字快速传达视觉效果
• 可用于对多种主题进行建模，只要它们包含关系结构

缺点

• 从更高层次来看，将文本转换为图像可能非常耗时。
• 很难看到现有的边或给定顶点连接到它的边数

应用

• 网络表示
• 建模社交网络，例如 Facebook。

如需更深入的解释，请参阅我们关于图表的 Edpresso 文章！

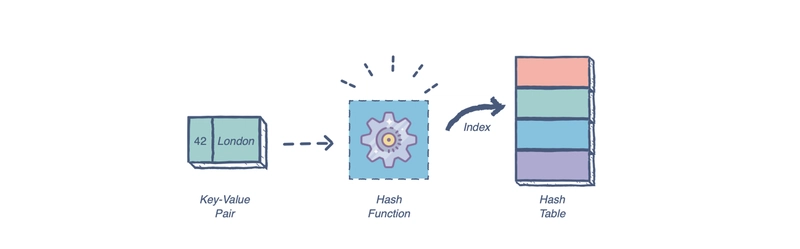
哈希表（地图）

哈希表是一种复杂的数据结构，能够存储大量信息并高效地检索特定元素。这种数据结构依赖于键/值对的概念，其中“键”是要搜索的字符串，“值”是与该键配对的数据。

每个被搜索的键都会使用预定义的哈希函数从其字符串形式转换为数值，称为哈希值。然后，该哈希值指向一个存储桶——表中一个较小的子组。然后，它会在存储桶中搜索最初输入的键，并返回与该键关联的值。

优势

• 键可以是任意形式，但数组的索引必须是整数
• 高效的搜索功能
• 每次搜索的操作次数固定
• 插入或删除操作的恒定成本

缺点

• 冲突：当两个键转换为相同的哈希码或两个哈希码指向相同的值时导致的错误。
• 这些错误很常见，通常需要彻底检查哈希函数。

应用

• 数据库存储
• 按名称查找地址

每个哈希表都可能存在很大差异，从键和值的类型，到哈希函数的工作方式，都各不相同。由于这些差异以及哈希表的多层性，几乎不可能进行如此通用的封装。

如需更深入的解释，请参阅我们关于哈希表的 Edpresso 文章！

继续学习。

无需费力浏览视频或文档，即可学习 JavaScript 数据结构。Educative 的文本课程易于浏览，并配备实时编程环境，让学习快速高效。JavaScript
数据结构：面试复习

数据结构面试题

对于许多开发人员和程序员来说，数据结构对于顺利通过编程面试至关重要。数据结构相关的问题和难题是现代编程面试的基石。事实上，它们对你能否被录用以及作为候选人的入职率有着举足轻重的影响。

今天，我们将讨论 JavaScript 数据结构的七个常见编程面试问题，每个问题都对应我们上面讨论过的每种数据结构。每个问题还将基于 BigO 符号理论讨论其时间复杂度。

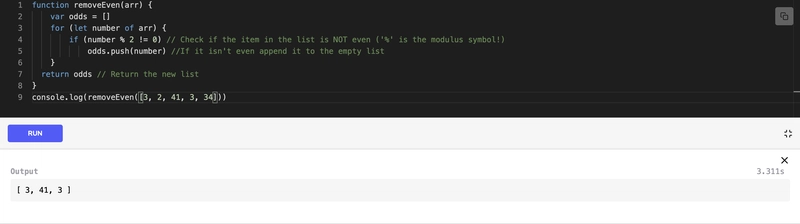
数组：从数组中删除所有偶数

问题陈述：实现一个函数removeEven(arr)，该函数以数组 arr 作为输入，并从给定数组中删除所有偶数元素。

输入：随机整数数组

[1,2,4,5,10,6,3]

输出：仅包含奇数的数组

[1,5,3]

在面试中，有两种方法可以解决这个编码问题。让我们分别讨论一下。

解决方案 #1：“手动”完成

该方法从数组的第一个元素开始。如果当前元素不是偶数，则将其推送到新数组中。如果是偶数，则移动到下一个元素，重复此操作直至到达数组末尾。由于需要迭代整个数组，因此该解决方案的时间复杂度为O(n)。

解决方案＃2：使用 filter() 和 lambda 函数

此解决方案同样从第一个元素开始，检查它是否为偶数。如果是偶数，则过滤掉该元素。如果不是，则跳到下一个元素，重复此过程，直到到达数组末尾。

过滤器函数使用 lambda 或箭头函数，它们的语法更短、更简单。过滤器会过滤掉 lambda 函数返回 false 的元素。其时间复杂度与上一个解决方案的时间复杂度相同。

堆栈：使用堆栈检查括号是否平衡

问题描述：实现一个isBalanced()函数，用于获取一个仅包含花括号{}、方括号[]和圆括号的()字符串。该函数应该告诉我们字符串中所有括号是否匹配。这意味着每个左括号都会有一个右括号。例如，{[]}是匹配的，但{[}]是不匹配的。

输入：(仅由、)、{、和}组成的字符串[]

exp = "{[({})]}"

输出：False如果表达式没有匹配的括号，则返回。如果匹配，则函数返回True。

True

为了解决这个问题，我们可以简单地使用字符堆栈。查看下面的代码来了解它是如何工作的。

"use strict";
const Stack = require('./Stack.js');

function isBalanced(exp) {
    var myStack = new Stack();
    //Iterate through the string exp
    for (var i = 0; i < exp.length; i++) {
        //For every closing parenthesis check for its opening parenthesis in stack


        if (exp[i] == '}' || exp[i] == ')' || exp[i] == ']') {

            if (myStack.isEmpty()) {

                return false
            }
            let output = myStack.pop();
            //If you can't find the opening parentheses for any closing one then returns false.
            if (((exp[i] == "}") && (output != "{")) || ((exp[i] == ")") && (output != "(")) || ((exp[i] == "]") && (output != "["))) {
                return false;
            }

        } else {
            //For each opening parentheses, push it into stack
            myStack.push(exp[i]);
        }

    }
    //after complete traversal of string exp, if there's any opening parentheses left
    //in stack then also return false.
    if (myStack.isEmpty() == false) {
        return false
    }
    //At the end return true if you haven't encountered any of the above false conditions.
    return true
}


var inputString = "{[()]}"
console.log(inputString)
console.log(isBalanced(inputString))

inputString = "{[([({))]}}"
console.log(inputString)
console.log(isBalanced(inputString))

输出：
{[()]}
true
{[([({))]}}
false

要查看此解决方案的其余代码，请前往Educative.io在嵌入式环境中运行代码。

这个过程将逐个字符地遍历字符串。我们可以根据两个因素判断字符串是否不平衡：

1. 堆栈是空的。
2. 堆栈顶部元素的类型不正确。

如果其中一个条件成立，则返回False。
如果括号是左括号，则将其压入堆栈。如果最后所有括号都平衡，则堆栈为空。如果不为空，则返回False。由于我们只遍历字符串 exp 一次，因此时间复杂度为O(n)。

队列：生成从 1 到 n 的二进制数

问题描述：实现一个函数，该函数将使用队列以字符串的形式生成从到的findBin(n)二进制数。1n

输入：一个正整数 n

n = 3

输出：以字符串形式返回二进制数，1最多n

result = ["1","10","11"]

解决这个问题最简单的方法是使用队列，根据之前的数字生成新的数字。我们来分解一下。

"use strict";
const Queue = require('./Queue.js');
function findBin(n) {
    let result = [];
    let myQueue = new Queue();
    var s1, s2;
    myQueue.enqueue("1");
    for (var i = 0; i < n; i++) {

        result.push(myQueue.dequeue());
        s1 = result[i] + "0";
        s2 = result[i] + "1";

        myQueue.enqueue(s1);
        myQueue.enqueue(s2);

    }

    return result;
}

console.log(findBin(10))

输出：
['1','10','11','100','101','110','111','1000','1001','1010']

要查看此解决方案的其余代码，请前往Educative.io在嵌入式环境中运行代码。

关键在于通过在前一个二进制数后添加 0 和 1 来生成连续的二进制数。具体来说，

• 如果将 0 和 1 附加到 1，则可以生成 10 和 11。
• 如果在 10 后附加 0 和 1，则会生成 100 和 101。

一旦我们生成一个二进制数，它就会被放入队列中，这样，当我们在该数字即将入队时，只要我们附加 0 和 1，就可以生成新的二进制数。由于队列遵循先进先出的特性，入队的二进制数会被出队，这样生成的数组在数学上就是正确的。

看看上面的代码。在第 7 行，1被入队。为了生成二进制数序列，我们将一个数字从队列中取出并存储在数组 中result。在第 11-12 行，我们附加0和1来生成下一个数字。这些新数字也在第 14-15 行入队。队列接收整数值，因此在入队时会将字符串转换为整数。

该解决方案的时间复杂度为O(n)O(n)，因为常数时间操作执行了 n 次。

链表：反转链表

问题描述：编写reverse函数获取单链表并将其反转到位。

输入：单链表

LinkedList = 0->1->2->3-4

输出：反向链接列表

LinkedList = 4->3->2->1->0

解决这个问题最简单的方法是使用迭代指针操作。我们来看一下。

"use strict";
const LinkedList = require('./LinkedList.js');
const Node = require('./Node.js');

function reverse(list) {
  let previousNode = null;
  let currentNode = list.getHead(); // The current node
  let nextNode = null; // The next node in the list

  //Reversal
  while (currentNode != null) {
    nextNode = currentNode.nextElement;
    currentNode.nextElement = previousNode;
    previousNode = currentNode;
    currentNode = nextNode;
  }

  //Set the last element as the new head node
  list.setHead(previousNode);

}

let list = new LinkedList();
list.insertAtHead(4);
list.insertAtHead(9);
list.insertAtHead(6);
list.insertAtHead(1);
list.insertAtHead(0);
list.printList();
reverse(list);
list.printList();

输出：
0 -> 1 -> 6 -> 9 -> 4 -> null
4 -> 9 -> 6 -> 1 -> 0 -> null

要查看此解决方案的其余代码，请前往Educative.io在嵌入式环境中运行代码。

我们使用循环遍历输入列表。对于一个current节点，它与该节点的链接previous被反转。然后，next将下一个节点存储在列表中。让我们逐行分解。

• 第 22 行-将current节点存储nextElement在next
• 第 23 行 -current将节点设置nextElement为previous
• 第 24 行 - 将节点设为下一次迭代的current新节点previous
• 第 25 行 - 用于next转到下一个节点
• 第 29 行 - 我们将head指针重置为指向最后一个节点

由于列表仅遍历一次，因此该算法在O(n)中运行。

树：在二叉搜索树中查找最小值

问题描述：使用findMin(root)函数在二叉搜索树中查找最小值。

输入：二叉搜索树的根节点

bst = {
    6 -> 4,9
    4 -> 2,5
    9 -> 8,12
    12 -> 10,14
}
where parent -> leftChild,rightChild

输出：二叉搜索树中的最小整数值

2

让我们看看这个问题的一个简单解决方案。

解决方案：迭代findMin( )

此解决方案首先检查根是否为null。null如果是，则返回。然后，它移动到左子树，并继续处理每个节点的左孩子，直到到达最左孩子。

"use strict";
const BinarySearchTree = require('./BinarySearchTree.js');
const Node = require('./Node.js');

function findMin(rootNode)
{
  if(rootNode == null)
    return null;
  else if(rootNode.leftChild == null)
      return rootNode.val
  else
    return findMin(rootNode.leftChild)
}  
var BST = new BinarySearchTree(6)
BST.insertBST(20)
BST.insertBST(-1)

console.log(findMin(BST.root))

输出：
-1

要查看此解决方案的其余代码，请前往Educative.io在嵌入式环境中运行代码。

图表：移除边

问题描述：实现 removeEdge 函数，以源和目标作为参数。它应该检测它们之间是否存在边。

输入：图表、源和目标

输出：删除源和目标之间的边的图。

removeEdge(graph, 2, 3)

这个问题的解决方案相当简单：我们使用索引和删除。看一下

"use strict";
const LinkedList = require('./LinkedList.js');
const Node = require('./Node.js');
const Graph = require('./Graph.js');

function removeEdge(graph, source, dest){
  if(graph.list.length == 0){
    return graph;
  }

  if(source >= graph.list.length || source < 0){
    return graph;
  }

  if(dest >= graph.list.length || dest < 0){
    return graph;
  }

  graph.list[source].deleteVal(dest);
  return graph;
}


let g = new Graph(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(2, 4);
g.addEdge(4, 0);
console.log("Before removing edge")
g.printGraph();

removeEdge(g, 1, 3);

console.log("\nAfter removing edge")
g.printGraph();

要查看此解决方案的其余代码，请前往Educative.io在嵌入式环境中运行代码。

由于顶点存储在数组中，我们可以访问source链表。然后调用delete链表函数。由于可能需要遍历 E 条边，因此该解决方案的时间复杂度为 O(E)。

哈希表：将最大堆转换为最小堆

问题描述：convertMax(maxHeap)实现将二进制最大堆转换为二进制最小堆的函数。maxHeap应为格式的数组maxHeap，即父级大于其子级。

输入：最大堆

maxHeap = [9,4,7,1,-2,6,5]

输出：返回转换后的数组

result = [-2,1,5,9,4,6,7]

为了解决这个问题，我们必须对所有父节点进行最小堆化。我们来看一下。

我们将 视为maxHeap一个常规数组，并对其进行重新排序，使其能够准确地表示最小堆。您可以在上面的代码中看到这一过程。convertMax()然后，该函数通过调用该函数，从最低父节点开始恢复所有节点的堆属性minHeapify()。就时间复杂度而言，此解决方案需要O(nlog(n)) 的时间。

资源

说到 JavaScript 中的数据结构，显然有很多东西需要学习。因此，我们整理了这份资源列表，帮助您快速掌握所需的知识。

文章

• JavaScript ES6 教程：刷新你的 JavaScript 技能并了解 ES6 及更高版本的所有新内容
• 5 种经过实践检验的编码面试准备技巧：向专家学习有关准备和执行编码面试的技巧
• StackOverflow JavaScript 数据结构库：一个发现有用库（如 JSClass、Buckets 等）的绝佳资源

课程

• JavaScript 数据结构：面试复习指南：这是一本面向所有 JavaScript 数据结构初学者的权威指南。本书包含超过 160 个代码练习和 60 个实践挑战，并详细回顾了所有数据结构及其实现。
• JavaScript 中的数据结构 - 可视化与练习：想要更多动手实践？本课程通过简单的可视化效果和测验，深入探讨数据结构问题的核心。
• 精通 JavaScript 面试：掌握数据结构技能后，是时候复习一下所有与 JavaScript 面试相关的知识了。本课程涵盖了所有内容。

图书

• 学习 JS 数据结构和算法：通过解决显著的编程问题，牢牢掌握所有流行的数据结构
• 免费 Code Champ 数据结构书籍列表：跳过搜索并参考这份最推荐的 JS 数据结构和算法书籍的有用列表