对“大O”符号的精彩阐释

2025-06-04

对“大O”符号的精彩阐释

了解如何使用大 O 符号来衡量算法性能。

大O（Big O）是计算机科学领域的一个基本概念，但大多数人并不理解它是什么以及它的重要性。对于初学者来说，掌握它也非常困难。在本文中，我们将揭开大O的神秘面纱，理解它的重要性，并探索如何利用它来确定算法的效率。

先决条件

  • 对数组等数据结构有基本的了解。

  • JavaScript 基础知识（我们的示例采用 JavaScript 语法）

什么是 Big O？

图片描述

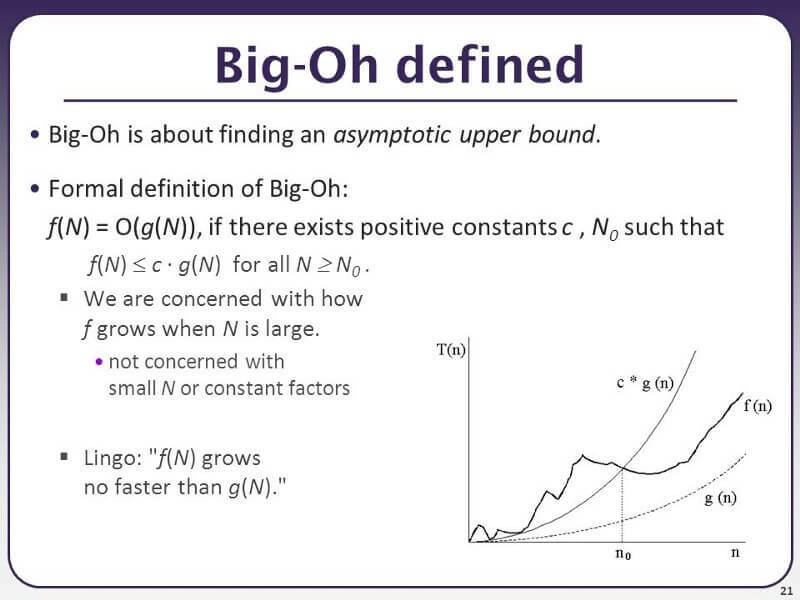
上面这幅图把大 O 解释为“寻找渐近上限”，但这不是我们来这里的目的，我们来这里是为了一个更简单的解释，而不是这个😂😂😂😂。那就让我们来定义它吧。

大 O 是一种表达和表示算法性能的方式。算法是一种逐步解决问题的方法，重要的是要知道，一个问题可以有多种算法来找到它的解决方案，大 O 符号是识别最优/有效算法的标准。

大 O 衡量算法性能的两个因素是：完成所需的时间和消耗的内存量。也就是说，使用大 O 衡量任何算法的性能有两种方法：

  • 时间复杂度。
  • 空间复杂度。

时间复杂度

时间复杂度是指算法实现其目标的速度。简单来说，它指的是算法完成目标所需的时间，取决于算法在操作次数增加时的性能表现。

空间复杂度

这是指算法在执行其所需任务时所消耗的内存量。算法的空间复杂度取决于解决计算问题实例所需的内存空间量。

Big O的重要性

大 O 的一个主要意义在于它作为算法比较的标准。如前所述，可以使用多种算法来解决单个问题，而大 O 是一种确定解决该问题的最有效算法的方法。

Big O 的其他目标包括：

  • 根据算法的输入大小确定算法的最坏运行时间。

  • 从可扩展性和效率的角度分析算法。

大 O 符号的类型

有几种大 O 符号，但在深入研究它们之前，让我们先分析一下下面的图像。

图片描述

该图像是用于表示大 O 符号的格式，可以分为以下两个部分。

  • O，代表 Big O
  • n，代表操作次数。

注意：操作数表示算法处理的任务/活动数。

借助下图，我们将讨论大 O 符号的类型，同时重点关注最佳的三 (3) 种符号。

图片描述

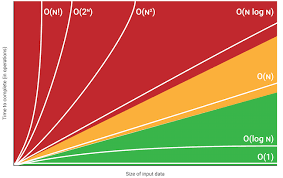
上图是显示几个 Big O 符号的图表，颜色代表以下内容；

  • 红色🟥区域代表任何算法的最坏情况。在这个区域中，我们有 O(N!)、O(N²)、O(2ⁿ) 和 O(N log N) 符号。

  • 黄色🟨区域代表任何算法的中级场景。与红色区域中的算法相比，此区域中的任何算法都是合适的且可以接受的。它由 O(N) 表示法组成。

  • 绿色🟩区域代表任何算法的最佳情况。这是每个算法的理想状态，它由 O(1) 和 O(log N) 表示法组成。

现在让我们深入研究黄色和绿色区域，它们由以下符号组成；

  • O(1) - 常数复杂度
  • O（N）——线性复杂度
  • O（Log N）——对数复杂度

O(1) - 恒定复杂度

恒定时间算法遵循 O(1) 表示法，这意味着它们的时间复杂度是恒定的。无论输入量多少，恒定时间算法的运行时间都相同。

因此，如果您得到；

  • 输入1次，1秒运行

  • 10个输入，1秒内运行

  • 100,000个输入，它将在1秒内运行。

我们来看一个代码示例。

const example1 = function (names) {
  console.log(names[0]);
};

example1(["Aahil", "grace", "joseph", "matilda", "patience", "Austin"]);
Enter fullscreen mode Exit fullscreen mode

在上面的例子中，我们创建了一个名为 的函数example1，它接受一个姓名数组作为输入。该函数只执行一项操作，即在浏览器控制台中打印数组中的第一个姓名。

输出👇

图片描述

上面这个例子的时间复杂度是常数，也就是说，无论输入是什么，它执行的操作数都是常数。也就是说，即使我们要查找数组中的第三个名字和最后一个名字，它的时间复杂度仍然是常数，因为它执行的仍然是从数组中查找名字的相同操作。

注意： O（1）是任何算法的最佳情况。

O（N）——线性复杂度

一个算法的复杂度为 O(N)，其复杂度随着输入数量的增加而变化。随着输入的增加，算法所需的时间也会相应增加。

因此，如果您获得；

  • 1个输入，就进行1个操作。

  • 10个输入，将执行10个操作。

  • 10万次输入，将进行10万次运算。

它在时间或空间复杂度上都具有线性性能。随着输入数量的增加，操作数量也会增加，完成所需的时间也会增加。

例如，阅读一本书时，所需的时间取决于这本书的页数。因此，阅读一本 10 页的书比阅读一本 1000 页的书所需的时间要短。这是一个更容易理解的例子，现在我们来看一个实际的代码示例。

const example2 = function (names) {
  for (const name of names) console.log(name);
};

example2(["Aahil", "grace", "joseph", "matilda", "patience", "Austin"]);
Enter fullscreen mode Exit fullscreen mode

在上面的例子中，我们创建了一个名为 的函数example2，该函数以姓名数组作为输入。该函数包含一个for...of循环，循环遍历姓名数组，并将数组中的每个姓名打印到控制台。该函数的输入参数是一个包含 6 个姓名的数组。

输出👇

图片描述

在这个例子中，如果向数组中添加更多的名称，则需要更长的时间才能完成，因此我们可以说它具有线性时间复杂度。

就空间复杂度而言，我们只创建了一个变量，但该变量占用的空间相当于将所有名称存储在数组中。因此，随着数组中名称的增加，变量的大小也会增加。

O（Log N）——对数复杂度

在复杂度为 O(log N) 的算法中，随着输入规模的增加，运算次数的增长非常缓慢。即使输入规模呈指数增长，计算时间也几乎不会增加。

因此，如果您获得；

  • 输入1次，1秒运行

  • 10个输入，2秒内运行。

  • 100个输入，3秒内运行完成。

注意：以下是关于O(log N)需要注意的几点；

  • O(log N) 的一个例子是二分查找。
  • 它的性能比 O(N) 算法高得多。

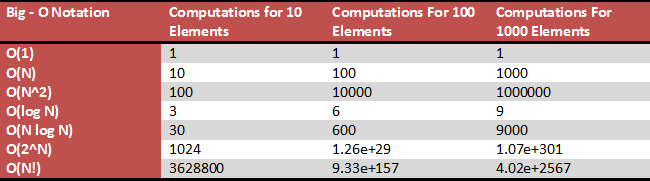
下面是一个汇总表，解释了大多数 Big O 符号的性质

图片描述

在上表中，我们可以看到，红色区域中的符号（例如 O(N!)）未经优化，并且无论输入数量多少，它们都会在空间和时间方面产生非常大的复杂度。红色区域中符号的算法在给定大量输入时需要更长的时间才能完成，并且会占用大量空间/内存。因此，建议在解决问题时对具有此类符号的算法进行优化或忽略。

值得注意的是，O(1) 是算法所能达到的最佳性能。大多数算法都可以通过优化达到上图所示的黄色或绿色区域，即 O(1)、O(log N) 和 O(N)，具体取决于某些权衡。

结论

当我们得出本文的结论时，希望我们能够实现一开始设定的所有目标，我想得出这样的结论：大 O 符号表示算法在处理大型问题（例如排序或搜索大型列表）时的表现如何。

文章来源：https://dev.to/aahil13/big-o-notation-56lg
Devto 翻译
PREV
Docker，从零开始🐋
NEXT
学习基本的 Web 组件