世界首个具有 O(0) 时间复杂度的静态时间正则表达式引擎
那到底是什么?
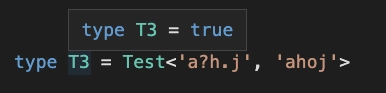
RegEx用静态类型编写的引擎?!- 代码
RegEx在编译时评估“模板”,以便您在运行应用程序之前知道结果?! RegExO(0)与运行时复杂性相关的引擎?!- 最小化 0 比特(GZip)长度输出?!
- 完全有缺陷,还未准备好投入生产?!
我没有开玩笑!!!这不仅仅是一个梦!
这是世界上第一个RegEx用纯 Typescript 类型编写的引擎。
检查工作示例!
Github 仓库 - ts-generics-RegEx-engine
免责声明
- 该代码尚未准备好在生产环境中使用。
- 由于 Typescript 的堆栈限制,一些
regExs 会因为太长而停止工作并触发递归堆栈溢出(称为)Type instantiation is excessively deep and possibly infinite。 RegEx回溯尚未实现。- 该解析器仅支持PCRE标准的一小部分,具体来说就是
.?*+()\\符号。
动机+使用
得益于 Typescript 4.1.x 的新功能,我们能够将字符串解析为一个包含标记的元组,甚至更多!因此,我决定RegEx仅使用 Typescript 静态类型编写自己的自定义引擎,以展示 Typescript 类型系统的强大功能。
RegEx 引擎在底层如何工作?
你可能知道,编程语言由编译器 + 解释器组成。它们非常复杂,包括词法分析器、解析器、解释器等等。
另一方面,这个小引擎相当简单,所以只有 3 个小模块:
- 1. 标记器
- 2. 解析器
- 3. 解释器
1. 标记器
小型通用程序type TokenizeString<T>只是将RegEx模板解析为标记,用作2. Parser构建RegEx抽象语法树 (AST) 的输入。
例子:
type T0 = TokenizeString<'\\(+(ab)+'>
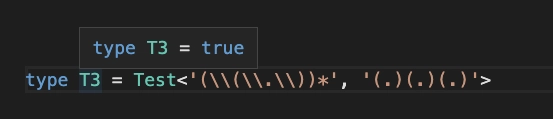
type T1 = TokenizeString<'\\(+(a(xy)+(xx)b)+'>
2. 解析器
type ParseRegExTokens<T> = ...采用标记化的模板并进行语法分析,生成模板的抽象语法树 (AST) 模型RegEx。
例子:
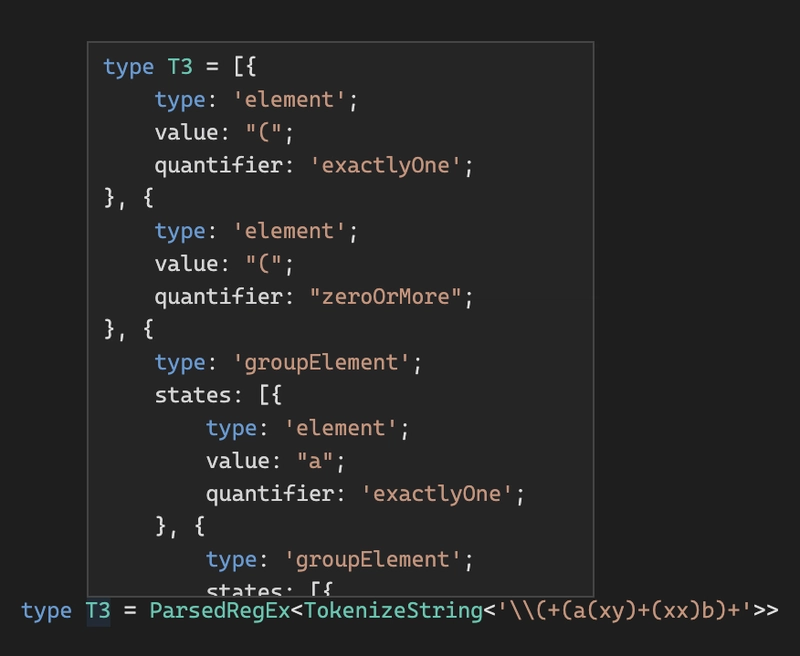
type T3 = ParsedRegEx<TokenizeString<'\\(+(a(xy)+(xx)b)+'>>
如您所见,解析器支持结构嵌套(如括号中的括号中的括号等......)
模板的 AST'\\(+(a(xy)+(xx)b)+'如下所示:
[{
type: 'element';
value: "(";
quantifier: 'exactlyOne';
}, {
type: 'element';
value: "(";
quantifier: "zeroOrMore";
}, {
type: 'groupElement';
states: [{
type: 'element';
value: "a";
quantifier: 'exactlyOne';
}, {
type: 'groupElement';
states: [{
type: 'element';
value: "x";
quantifier: 'exactlyOne';
}, {
type: 'element';
value: "y";
quantifier: 'exactlyOne';
}];
quantifier: 'exactlyOne';
}, {
...; // and so on
}, {
...; // and so on
}, {
...; // and so on
}];
quantifier: 'exactlyOne';
}]
3. 正则表达式解释器
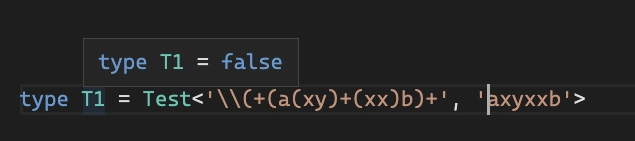
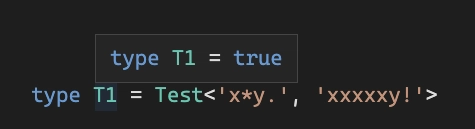
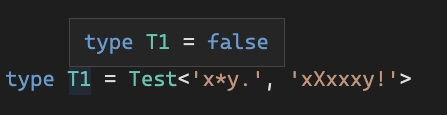
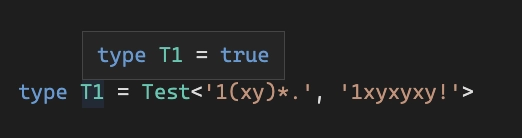
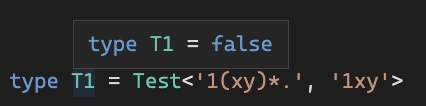
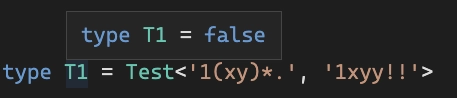
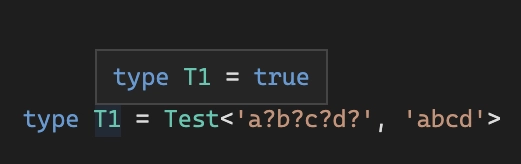
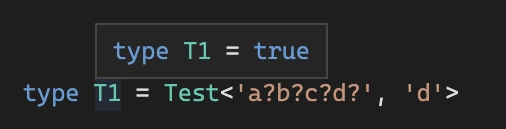
最后一步是创建一个适当的“解释器” type Test<RegExp, TestString> = ...,它通过应用 AST 中的规则来获取模板和测试字符串RegEx。
例子:
就这样!🎉 🎉
如果你不相信,你可以在这个 GitHub repo 中查看完整的源代码:https://raw.githubusercontent.com/Svehla/ts-generics-RegEx-engine
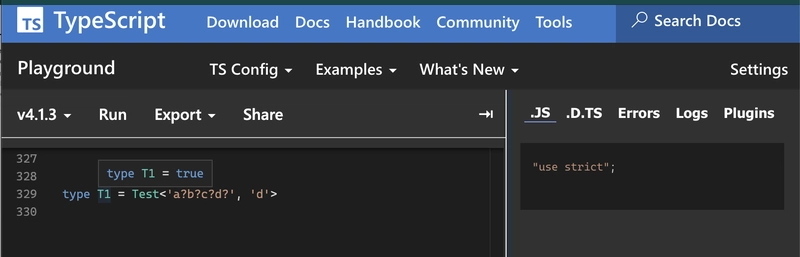
等等……实际输出结果如何Javascript?我们来看看吧!
哈哈!几百行静态类型,运行时输出却空空如也,O(0)时间复杂度也很高!这就是 Typescript 的魔力🦄
接下来呢?
如果您对 Typescript 类型系统的其他高级用法感兴趣,您可以查看这些关于如何创建一些高级 Typescript 泛型的分步文章/教程。
鏂囩珷鏉ユ簮锛�https://dev.to/svehla/world-first-static-time-regex-engine-with-o-0-time-complexity-4k4e 后端开发教程 - Java、Spring Boot 实战 - msg200.com
后端开发教程 - Java、Spring Boot 实战 - msg200.com